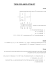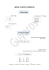הטכניון – מכון טכנולוגי לישראל, הפקולטה להנדסת מכונות

‫הטכניון – מכון טכנולוגי לישראל‪ ,‬הפקולטה להנדסת מכונות‬
‫‪TECHNION – Israel Institute of Technology, Faculty of Mechanical Engineering‬‬
‫תורת הבקרה )‪(035188‬‬
‫תרגול מס' ‪ – 6‬מרחב המצב‪ :‬קונטרולביליות ואובזרבביליות – פתרון‬
‫שאלה ‪1‬‬
‫‪q1‬‬
‫‪R1‬‬
‫‪q12‬‬
‫‪q2‬‬
‫‪h1‬‬
‫‪A1‬‬
‫‪R2‬‬
‫‪qout‬‬
‫‪h2‬‬
‫‪A2‬‬
‫איור ‪ :1‬מערכת לבקרת גובה נוזל במיכלים‬
‫באיור ‪ 1‬מתוארת מערכת לבקרת מפלסי מים ‪ h1 , h2‬בשני מכלי מים באמצעות הספיקות הנכנסות ‪ . q1 , q2‬נתון‪:‬‬
‫‪‬‬
‫‪ - A1  1, A2  0.5‬שטחי החתך של המכלים‪.‬‬
‫‪‬‬
‫‪ - R1  1, R2  1‬קבועי התנגדות השסתומים‪.‬‬
‫א‪ .‬כתבו מימוש פיזיקאלי למערכת כאשר ווקטור המצב הוא מפלסי המים במכלים‪.‬‬
‫פתרון שאלה ‪ 1‬סעיף א'‬
‫הפרש בין ספיקה נכנסת לספיקה יוצאת שווה לקצב שינוי נפח המים במיכל‪ .‬לכן משוואות המערכת הינן‬
‫‪q1  q12  V1  A1h1‬‬
‫‪q12  q2  qout  V2  A2 h2‬‬
‫מתוך חוקי זרימה בשסתומים ליניאריים‪:‬‬
‫‪h2‬‬
‫‪R2‬‬
‫נציב את ביטויי הספיקות היוצאות במשוואות המערכת‪ ,‬נציב ערכים מספריים ונקבל‪:‬‬
‫‪1‬‬
‫‪, qout ‬‬
‫‪h1‬‬
‫‪R1‬‬
‫‪q12 ‬‬
‫הטכניון – מכון טכנולוגי לישראל‪ ,‬הפקולטה להנדסת מכונות‬
‫‪TECHNION – Israel Institute of Technology, Faculty of Mechanical Engineering‬‬
‫‪1‬‬
‫‪1‬‬
‫‪‬‬
‫‪h1   R A h1  A q1  h1  q1‬‬
‫‪1 1‬‬
‫‪1‬‬
‫‪‬‬
‫‪‬‬
‫‪1‬‬
‫‪1‬‬
‫‪1‬‬
‫‪‬‬
‫‪h2  R A h1  R A h2  A q2  2h1  2h2  2q2‬‬
‫‪‬‬
‫‪1 2‬‬
‫‪2 2‬‬
‫‪2‬‬
‫ווקטור המצב הוא מפלסי המים ‪ x   h1 h2 ‬ווקטור הכניסות הוא הספיקות ‪ . u   q1 q2 ‬מימוש פיזיקאלי‪:‬‬
‫‪T‬‬
‫‪T‬‬
‫‪‬‬
‫‪ 1‬‬
‫‪‬‬
‫‪A‬‬
‫‪x 1‬‬
‫‪‬‬
‫‪1 ‬‬
‫‪‬‬
‫‪‬‬
‫‪ 0‬‬
‫‪R2 A2 ‬‬
‫‪‬‬
‫‪‬‬
‫‪0 ‬‬
‫‪1 0 ‬‬
‫‪1 0‬‬
‫‪ u  ‬‬
‫‪x‬‬
‫‪‬‬
‫‪u‬‬
‫‪1 ‬‬
‫‪ 2 2 ‬‬
‫‪0 2‬‬
‫‪A2 ‬‬
‫‪0‬‬
‫‪1‬‬
‫‪‬‬
‫‪ R A‬‬
‫‪1 1‬‬
‫‪x  Ax  Bu  ‬‬
‫‪ 1‬‬
‫‪ RA‬‬
‫‪ 1 2‬‬
‫המטריצה ‪ A‬משולשת‪ ,‬לכן הערכים העצמיים שלה הם אברי האלכסון‪:‬‬
‫‪1‬‬
‫‪R2 A2‬‬
‫‪, 2  ‬‬
‫‪1‬‬
‫‪R1 A1‬‬
‫‪1  ‬‬
‫ב‪ .‬האם ניתן לבקר את המפלסים על ידי שתי הספיקות? ועל ידי ספיקה בודדת?‬
‫פתרון שאלה ‪ 1‬סעיף ב'‬
‫‪1‬‬
‫‪ .1‬בקרה על ידי כניסה בודדת ‪. B    : q1‬‬
‫‪0‬‬
‫המערכת תהיה קונטרולבילית אם ורק אם יתקיים‪:‬‬
‫‪1‬‬
‫‪ n  2 ‬‬
‫‪0‬‬
‫‪0‬‬
‫‪  1‬‬
‫‪rank   I  A B  rank ‬‬
‫‪ 2   2‬‬
‫הדרגה יכולה לרדת רק אם ‪ ‬הוא ערך עצמי של ‪. A‬‬
‫‪1‬‬
‫‪2n‬‬
‫‪0‬‬
‫‪ 1 0‬‬
‫‪2  2 : rank ‬‬
‫‪ 2 0‬‬
‫‪,‬‬
‫‪1‬‬
‫‪2n‬‬
‫‪0‬‬
‫‪0‬‬
‫‪0‬‬
‫‪1  1: rank ‬‬
‫‪ 2 1‬‬
‫הדרגה לא יורדת עבור אף ע"ע‪ ,‬לכן כל המודים של המערכת קונטרולביליים והמערכת כולה קונטרולבילית‪.‬‬
‫‪0‬‬
‫‪ .2‬בקרה על ידי כניסה בודדת ‪. B    : q2‬‬
‫‪ 2‬‬
‫‪2‬‬
‫הטכניון – מכון טכנולוגי לישראל‪ ,‬הפקולטה להנדסת מכונות‬
‫‪TECHNION – Israel Institute of Technology, Faculty of Mechanical Engineering‬‬
‫המערכת תהיה קונטרולבילית אם יתקיים‪:‬‬
‫‪0‬‬
‫‪  1‬‬
‫‪rank   I  A B  rank ‬‬
‫‪ 2   2‬‬
‫‪0‬‬
‫‪ n ‬‬
‫‪2‬‬
‫נבדוק ירידת דרגה בערכים העצמיים של ‪. A‬‬
‫‪ 1 0‬‬
‫‪0‬‬
‫‪2n‬‬
‫‪2‬‬
‫‪2  2 : rank ‬‬
‫‪ 2 0‬‬
‫‪0‬‬
‫‪1 n‬‬
‫‪2‬‬
‫‪,‬‬
‫‪0‬‬
‫‪0‬‬
‫‪1  1: rank ‬‬
‫‪ 2 1‬‬
‫הדרגה יורדת עבור ‪ ,   1‬לכן המוד המתאים לע"ע זה אינו קונטרולבילי‪ ,‬אז המערכת כולה לא קונטרולבילית‪.‬‬
‫המשמעות הפיזיקאלית של מודים לא קונטרולביליים‪:‬‬
‫נחשב את הווקטורים העצמיים של מטריצה ‪. A‬‬
‫‪, 2  2 :  V2   0 1‬‬
‫‪T‬‬
‫‪1  1:  V1  1 2 ‬‬
‫‪T‬‬
‫הווקטורים העצמיים הם אופני התנודה של המערכת (מודים)‪ .‬תגובת המערכת לתנאי התחלה תהיה בכיוון של שילוב‬
‫של שני המודים‪ .‬אם תנאי ההתחלה בכיוון אחד המודים‪ ,‬רק מוד זה יעורר‪ .‬פתרון בזמן של ווקטור המצב הינו‪:‬‬
‫‪h20 ‬‬
‫‪T‬‬
‫‪x0   h10‬‬
‫‪t A t ‬‬
‫‪x  t   eAt x0   e  Bu   d‬‬
‫‪,‬‬
‫‪0‬‬
‫חישוב אקספוננט של המטריצה ‪: A‬‬
‫‪‬‬
‫‪‬‬
‫‪e2t ‬‬
‫‪‬‬
‫‪0‬‬
‫‪‬‬
‫‪‬‬
‫‪t‬‬
‫‪ 1 0 e‬‬
‫‪‬‬
‫‪‬‬
‫‪‬‬
‫‪t‬‬
‫‪2t‬‬
‫‪e2t   2 1   2 e  e‬‬
‫‪‬‬
‫‪t‬‬
‫‪1 0e‬‬
‫‪‬‬
‫‪‬‬
‫‪ 2 1  ‬‬
‫‪1‬‬
‫‪V2 ‬‬
‫‪ V1‬‬
‫‪ 1‬‬
‫‪‬‬
‫‪‬‬
‫‪t‬‬
‫‪‬‬
‫‪‬‬
‫‪2‬‬
‫‪  V1 V2  e‬‬
‫‪At‬‬
‫‪e‬‬
‫בקרה באמצעות ספיקה בודדת ‪: u  q1‬‬
‫‪  h  t  e t  ‬‬
‫‪ 10    ‬‬
‫‪2t ‬‬
‫‪e   h20  0  2 e t    e2 t  ‬‬
‫‪‬‬
‫‪‬‬
‫‪ 1‬‬
‫‪   q  d‬‬
‫‪2 t      1  ‬‬
‫‪e‬‬
‫‪0‬‬
‫‪‬‬
‫‪‬‬
‫‪‬‬
‫‪‬‬
‫‪ t ‬‬
‫‪2 t ‬‬
‫‪e    e   q1   d ‬‬
‫‪‬‬
‫‪0‬‬
‫‪‬‬
‫‪0‬‬
‫‪‬‬
‫‪‬‬
‫‪‬‬
‫‪‬‬
‫‪ et‬‬
‫‪x t   ‬‬
‫‪ 2 et  e2t‬‬
‫‪‬‬
‫‪‬‬
‫‪ h e t  t e  t   q   d‬‬
‫‪1‬‬
‫‪0‬‬
‫‪ 10‬‬
‫‪‬‬
‫‪t‬‬
‫‪ 2h10 et  e2t  h20e2t  2‬‬
‫‪0‬‬
‫‪‬‬
‫‪‬‬
‫‪‬‬
‫הכניסה ‪ q1‬משתתפת בביטוי של ‪ x1  t ‬ו ‪ , x2  t ‬לכן אנו שולטים על כל ווקטור המצב בלי קשר לתנאי ההתחלה‪.‬‬
‫‪3‬‬
‫הטכניון – מכון טכנולוגי לישראל‪ ,‬הפקולטה להנדסת מכונות‬
‫‪TECHNION – Israel Institute of Technology, Faculty of Mechanical Engineering‬‬
‫‪‬‬
‫בקרה באמצעות ספיקה בודדת ‪: u  q2‬‬
‫‪0‬‬
‫‪   q2   d‬‬
‫‪2 t ‬‬
‫‪e     2 ‬‬
‫‪0‬‬
‫‪  h10  t  e t  ‬‬
‫‪    ‬‬
‫‪e2t   h20  0  2e t    2e2 t  ‬‬
‫‪0‬‬
‫‪ e t‬‬
‫‪x t   ‬‬
‫‪ 2et  2e2t‬‬
‫‪‬‬
‫‪ h10et‬‬
‫‪‬‬
‫‪‬‬
‫‪‬‬
‫‪‬‬
‫‪t‬‬
‫‪ 2h10 et  e2t  h20e2t  2 e 2 t   q2   d ‬‬
‫‪0‬‬
‫‪‬‬
‫‪‬‬
‫‪‬‬
‫‪‬‬
‫הכניסה ‪ q2‬משתתפת רק ב ‪ , x2  t ‬לכן אין שליטה על ‪ x1  t  . x1  t ‬מורכב מתגובה לתנאי התחלה בלבד‪ ,‬ולכן‪:‬‬
‫‪-‬‬
‫כאשר תנאי ההתחלה בכיוון המוד ‪ , V1  1 2 ‬מתקיים‪:‬‬
‫‪T‬‬
‫‪ h10et‬‬
‫‪‬‬
‫‪‬‬
‫‪x t   ‬‬
‫‪t‬‬
‫‪ 2h10et  2 e2 t   q2   d ‬‬
‫‪0‬‬
‫‪‬‬
‫‪‬‬
‫‪‬‬
‫‪h20  2h10‬‬
‫‪‬‬
‫‪x0   1 2 ‬‬
‫‪T‬‬
‫משתנה המצב ‪ x1  t ‬מתנהג בזמן ללא שליטתנו‪ .‬לכן ‪ V1  1 2 ‬הוא מוד לא קונטרולבילי‪.‬‬
‫‪T‬‬
‫‪-‬‬
‫כאשר תנאי ההתחלה בכיוון המוד ‪ , V2   0 1‬מתקיים‪:‬‬
‫‪T‬‬
‫‪0‬‬
‫‪‬‬
‫‪‬‬
‫‪x t   ‬‬
‫‪t‬‬
‫‪ h20e2t  2 e2t   q2   d ‬‬
‫‪0‬‬
‫‪‬‬
‫‪‬‬
‫‪h10  0 ‬‬
‫‪‬‬
‫‪x0    0 1‬‬
‫‪T‬‬
‫כיוון ש ‪ , x1  t   0 t‬התגובה מורכבת מ ‪ x2  t ‬בלבד וכיוון שאנו שולטים עליה זהו מוד קונטרולבילי‪.‬‬
‫‪-‬‬
‫כיוון שבמקרה הכללי תנאי ההתחלה הם שילוב של שני המודים‪ ,‬המערכת הכוללת לא קונטרולבילית‪.‬‬
‫‪1 0‬‬
‫‪T‬‬
‫‪.B  ‬‬
‫‪ .3‬בקרה באמצעות שתי הספיקות‪ : u   q1 q2  ,‬‬
‫‪0 2‬‬
‫ברור כי אם המערכת קונטרולבילית עם הספיקה הבודדת ‪ , q1‬היא תישאר קונטרולבילית גם עם הוספת הספיקה ‪. q2‬‬
‫נאשש זאת על ידי חישוב מטריצת הקונטרולביליות‪.‬‬
‫‪ 1 0 1 0 ‬‬
‫‪C   B AB   ‬‬
‫‪  rank  C   2‬‬
‫‪ 0 2 2 4 ‬‬
‫‪4‬‬
‫הטכניון – מכון טכנולוגי לישראל‪ ,‬הפקולטה להנדסת מכונות‬
‫‪TECHNION – Israel Institute of Technology, Faculty of Mechanical Engineering‬‬
‫ג‪ .‬האם ניתן לשחזר את מפלסי המים במכלים על ידי מדידת שתי הספיקות היוצאות ‪ q12‬ו ‪ ? qout‬ועל ידי מדידת‬
‫ספיקה יוצאת בודדת?‬
‫פתרון שאלה ‪ 1‬סעיף ג'‬
‫‪ .1‬היציאה הנמדדת היא ‪ qout‬בלבד‪ .‬כאן ‪ , y  qout  h2 R2  h2‬לכן מטריצת היציאה היא ‪. C   0 1‬‬
‫מטריצת האובזרבביליות הינה‬
‫‪ C  0 1 ‬‬
‫‪O‬‬
‫‪‬‬
‫‪  rank  O   2‬‬
‫‪ CA   2 2 ‬‬
‫המערכת אובזרבבילית‪ .‬הספיקה ‪ qout‬כוללת מידע על מפלסי המים בשני המכלים שמעליה‪ ,‬לכן על ידי מדידת ‪qout‬‬
‫נוכל לשחזר את מפלס הנוזל בשני המכלים‪.‬‬
‫‪ .2‬היציאה הנמדדת היא ‪ q12‬בלבד‪ .‬כאן ‪ , y  q12  h1 R1  h1‬לכן מטריצת היציאה היא ‪ . C  1 0 ‬מטריצת‬
‫האובזרבביליות הינה‬
‫‪ C   1 0‬‬
‫‪O‬‬
‫‪‬‬
‫‪  rank  O   1‬‬
‫‪ CA   1 0 ‬‬
‫המערכת אינה אובזרבבילית‪ .‬לספיקה ‪ q12‬היוצאת מהמכל העליון בלבד אין מידע על מפלס המים במכל שמתחתיה‪ ,‬לכן‬
‫על ידי מדידת ‪ q12‬נוכל לשחזר רק את מפלס הנוזל במיכל העליון‪.‬‬
‫‪ .3‬היציאות הנמדדות הן ‪ q12‬ו ‪. qout‬‬
‫המערכת תהיה אובזרבבילית כי כל המידע נמצא כבר בספיקה היוצאת ‪ . qout‬למעשה‪ ,‬כאן אנו מודדים את ווקטור‬
‫המצב עצמו ולכן‬
‫‪1 0‬‬
‫‪C‬‬
‫‪‬‬
‫‪0 1‬‬
‫מטריצת האובזרבביליות הינה‬
‫‪1 0‬‬
‫‪‬‬
‫‪‬‬
‫‪0   h1   1 0 ‬‬
‫‪ C  0 1‬‬
‫‪   ‬‬
‫‪x‬‬
‫‪‬‬
‫‪O‬‬
‫‪‬‬
‫‪‬‬
‫‪ rank  O   2‬‬
‫‪‬‬
‫‪‬‬
‫‪ ‬‬
‫‪1  h‬‬
‫‪‬‬
‫‪0‬‬
‫‪1‬‬
‫‪CA‬‬
‫‪‬‬
‫‪1‬‬
‫‪0‬‬
‫‪‬‬
‫‪‬‬
‫‪‬‬
‫‪‬‬
‫‪‬‬
‫‪2‬‬
‫‪‬‬
‫‪R2 ‬‬
‫‪‬‬
‫‪‬‬
‫‪ 2 2 ‬‬
‫‪5‬‬
‫‪1‬‬
‫‪ q12   R1‬‬
‫‪y ‬‬
‫‪‬‬
‫‪ qout   0‬‬
‫הטכניון – מכון טכנולוגי לישראל‪ ,‬הפקולטה להנדסת מכונות‬
‫‪TECHNION – Israel Institute of Technology, Faculty of Mechanical Engineering‬‬
‫ד‪ .‬באפשרותנו למדוד את הספיקה ‪ . y  qout‬נתון וקטור מדידות ‪ y m  t ‬מרגע אפס ועד רגע ‪ . t f  4sec‬שחזרו‬
‫את וקטור המצב על ידי שחזור תנאי ההתחלה ‪ h10‬ו ‪. h20‬‬
‫פתרון שאלה ‪ 1‬סעיף ד'‬
‫גרמיאן האובזרבביליות נתון על ידי‬
‫‪tf‬‬
‫‪ ‬‬
‫‪P t f   eA  CT CeA d‬‬
‫‪T‬‬
‫‪0‬‬
‫עבור מערכת אובזרבבילית הגרמיאן איננו סינגולרי ומקבלים‪:‬‬
‫‪eA  CT y   d‬‬
‫‪T‬‬
‫‪  0‬‬
‫‪tf‬‬
‫‪x0  P 1 t f‬‬
‫אצלנו‪:‬‬
‫‪0.165 ‬‬
‫‪ 5.16 3.41‬‬
‫‪1‬‬
‫‪  P tf  ‬‬
‫‪‬‬
‫‪0.25 ‬‬
‫‪ 3.41 6.26 ‬‬
‫‪ ‬‬
‫‪e   e   2  e   e   ‬‬
‫‪‬‬
‫‪ 0.303‬‬
‫‪P t   ‬‬
‫‪d  ‬‬
‫‪‬‬
‫‪‬‬
‫‪ 0.165‬‬
‫‪ 2 e   e  ‬‬
‫‪‬‬
‫‪e ‬‬
‫‪‬‬
‫‪‬‬
‫‪‬‬
‫‪‬‬
‫‪ 5.16 3.41  2  e  e  ‬‬
‫‪‬‬
‫‪ y   d ‬‬
‫‪x ‬‬
‫‪4‬‬
‫‪2‬‬
‫‪3‬‬
‫‪4‬‬
‫‪4‬‬
‫‪2‬‬
‫‪m‬‬
‫‪‬‬
‫‪‬‬
‫‪‬‬
‫‪e2‬‬
‫שאלה ‪2‬‬
‫‪2qin‬‬
‫‪qin‬‬
‫‪qin‬‬
‫‪h2‬‬
‫‪h1‬‬
‫‪A2‬‬
‫‪A1‬‬
‫איור ‪ :2‬מערכת מכלים בשאלה ‪2‬‬
‫נתונה מערכת מכלים הניזונים מספיקה משותפת‪ ,‬כמתואר באיור ‪.2‬‬
‫א‪ .‬רשמו מימוש למערכת במרחב המצב‪.‬‬
‫‪6‬‬
‫‪2‬‬
‫‪4‬‬
‫‪‬‬
‫‪3‬‬
‫‪‬‬
‫‪6.26  0 ‬‬
‫‪‬‬
‫‪‬‬
‫‪42‬‬
‫‪0‬‬
‫‪‬‬
‫‪ 3.41‬‬
‫‪f‬‬
‫‪0‬‬
‫הטכניון – מכון טכנולוגי לישראל‪ ,‬הפקולטה להנדסת מכונות‬
‫‪TECHNION – Israel Institute of Technology, Faculty of Mechanical Engineering‬‬
‫פתרון שאלה ‪ 2‬סעיף א'‬
‫‪1‬‬
‫‪1‬‬
‫‪‬‬
‫‪h‬‬
‫‪‬‬
‫‪‬‬
‫‪h‬‬
‫‪‬‬
‫‪qin‬‬
‫‪1‬‬
‫‪1‬‬
‫‪‬‬
‫‪R‬‬
‫‪A‬‬
‫‪A‬‬
‫‪1 1‬‬
‫‪1‬‬
‫‪‬‬
‫‪ ‬‬
‫‪1‬‬
‫‪1‬‬
‫‪‬‬
‫‪h2   R A h2  A qin‬‬
‫‪‬‬
‫‪2 2‬‬
‫‪2‬‬
‫‪h1‬‬
‫‪‬‬
‫‪qout _1  R‬‬
‫‪‬‬
‫‪1‬‬
‫‪, ‬‬
‫‪h2‬‬
‫‪q‬‬
‫‪out _ 2 ‬‬
‫‪‬‬
‫‪R2‬‬
‫‪qin  qout _1  V1  A1h1‬‬
‫‪‬‬
‫‪‬‬
‫‪qin  qout _ 2  V2  A2 h2‬‬
‫ווקטור המצב הוא מפלסי המים ‪ x   h1 h2 ‬והכניסה היא ‪ . u  qin‬המימוש במרחב המצב הינו‪:‬‬
‫‪T‬‬
‫‪‬‬
‫‪ 1 ‬‬
‫‪‬‬
‫‪A ‬‬
‫‪x   1 u‬‬
‫‪ 1 ‬‬
‫‪1 ‬‬
‫‪‬‬
‫‪‬‬
‫‪A ‬‬
‫‪R2 A2 ‬‬
‫‪ 2‬‬
‫‪0‬‬
‫‪1‬‬
‫‪‬‬
‫‪ R A‬‬
‫‪1 1‬‬
‫‪x  Ax  Bu  ‬‬
‫‪‬‬
‫‪ 0‬‬
‫‪‬‬
‫ב‪ .‬האם קיימת כניסה המעבירה את המערכת מהמצב ההתחלתי למצב כלשהו ברגע מסוים?‬
‫פתרון שאלה ‪ 2‬סעיף ב'‬
‫למעשה שואלים האם המערכת קונטרולבילית‪ .‬נחשב את מטריצת הקונטרולביליות‪.‬‬
‫‪1 ‬‬
‫‪R1 A12 ‬‬
‫‪1  1‬‬
‫‪1 ‬‬
‫‪  det M C   1  1‬‬
‫‪‬‬
‫‪‬‬
‫‪‬‬
‫‪‬‬
‫‪2‬‬
‫‪2‬‬
‫‪1 ‬‬
‫‪A1 A2  R1 A1 R2 A2 ‬‬
‫‪R2 A1 A2 R1 A2 A1‬‬
‫‪‬‬
‫‪‬‬
‫‪R2 A22 ‬‬
‫‪‬‬
‫‪1‬‬
‫‪A‬‬
‫‪1‬‬
‫‪MC   B AB   ‬‬
‫‪1‬‬
‫‪A‬‬
‫‪ 2‬‬
‫הדטרמיננט מתאפס כאשר ‪ R1 A1  R2 A2‬ואז המערכת תהיה לא קונטרולבילית‪ .‬מהי המשמעות של תוצאה זו?‬
‫הפתרון בזמן‪:‬‬
‫‪t‬‬
‫‪A t ‬‬
‫‪x  t   e x0   e  Bu   d‬‬
‫‪At‬‬
‫‪0‬‬
‫כיוון שמטריצה ‪ A‬אלכסונית‪ ,‬מקבלים‪:‬‬
‫‪‬‬
‫‪‬‬
‫‪ R 1A t ‬‬
‫‪e 22 ‬‬
‫‪0‬‬
‫ופתרון וקטור המצב בזמן הינו‪:‬‬
‫‪7‬‬
‫‪e R11A1 t‬‬
‫‪‬‬
‫‪‬‬
‫‪ 0‬‬
‫‪At‬‬
‫‪e‬‬
‫ הפקולטה להנדסת מכונות‬,‫הטכניון – מכון טכנולוגי לישראל‬
TECHNION – Israel Institute of Technology, Faculty of Mechanical Engineering
t

1  R 1A 
 x1  t    e 1 1 u  t    d
A

0 1

t

1  R21A2 
x
t

u  t    d
 2   e
A

2
0
:‫ מקבלים‬R1 A1  R2 A2 ‫עבור‬
t
x2  t   
0
A
R
1  R11A1
e
u  t    d  1 x1  t   2 x1  t 
A2
A2
R1
‫ מקרה‬.‫ לכן לא נוכל על ידי אותה כניסה להגיע לכל מצב שנרצה‬,‫במצב זה הגובה במיכל השני פרופורצינאלי לראשון‬
. x1  t   x2  t  t ‫ שאז‬, A1  A2 ‫ ו‬R1  R2 ‫פרטי הוא כאשר‬
‫ נניח‬.‫ לכן קיימת כניסה המביאה את המערכת לכל מצב שהוא‬,‫ המערכת כן קונטרולבילית‬R1 A1  R2 A2 ‫עבור‬

, u(t )  1 1(t )  ( 2  1 ) 1(t  T / 2) ‫למשל כניסה מהצורה‬
u(t)
2
1
t
T/2
T
:‫ נקבל שתי משוואות בשני נעלמים‬.  H1
H 2  ‫ להיות‬t  T ‫נרצה להביא את הגבהים במכלים ברגע‬
T
 T
 T
 T
x1 T    R1 (e 2 A1R1  e A1R1 )   2   R1 (1  e 2 A1R1 )  1  H1




T
T
T



x2 T    R2 (e 2 A2 R2  e A2 R2 )   2   R2 (1  e 2 A2 R2 )  1  H 2




8