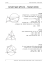מעגל החוסם משולש

Transcription

מעגל החוסם משולש

‫מעגל החוסם משולש‬
‫מעגל החוסם משולש הוא מעגל העובר דרך שלושת קדקודי המשולש ‪.‬‬
‫קיים משפט ש לפיו ‪ :‬כל משולש אפשר לחסום במעגל ‪.‬‬
‫‪A‬‬
‫במילים אחרות ‪ ,‬אם נתון משולש ‪ABC‬‬
‫אז קיים תמיד מעגל העובר דרך‬
‫הקדקודים ‪ B , A‬ו‪ C -‬של המשולש ‪.‬‬
‫מעגל זה נקרא המעגל החוסם את המשולש ‪.‬‬
‫הערות ‪ ( 1 ) :‬כאשר המעגל‬
‫חסום‬
‫חוסם‬
‫‪C‬‬
‫‪B‬‬
‫את המשולש ‪ ,‬אפשר לומר שהמשולש‬
‫במעגל ‪.‬‬
‫) ‪ ( 2‬לכל משולש קיים רק מעגל אחד החוסם אותו ‪.‬‬
‫משפט ‪ :‬נקודת מפגש האנכים האמצ עיים לצלעות המשולש היא מרכז‬
‫המעגל החוסם את המשולש ‪.‬‬
‫בציור מתואר משולש ‪. ABC‬‬
‫‪A‬‬
‫שלושת האנכים האמצעיים‬
‫‪O‬‬
‫לצלעות המשולש נפגשים‬
‫בנקודה ‪ , O‬שהיא מרכז‬
‫‪C‬‬
‫המעגל החוסם את המשולש ‪.‬‬
‫‪B‬‬
‫הערות ‪:‬‬
‫‪A‬‬
‫א ‪ .‬אם המשולש הוא חד‪ -‬זווית ‪,‬‬
‫אז מרכז המעגל החוסם‬
‫את המשולש נמצא בתוך‬
‫המשולש ‪ ,‬ולהיפך ‪.‬‬
‫‪C‬‬
‫‪B‬‬
‫‪A‬‬
‫ב ‪ .‬אם המשולש הוא ישר‪ -‬זווית ‪,‬‬
‫‪B‬‬
‫‪C‬‬
‫את המשולש נמצא באמצע‬
‫היתר ‪ ,‬ולהיפך ‪.‬‬
‫ג ‪ .‬אם המשולש הוא קהה זווית ‪,‬‬
‫‪A‬‬
‫‪C‬‬
‫‪B‬‬
‫את המשולש נמצא מחוץ‬
‫למשולש ‪ ,‬ולהיפך ‪.‬‬
‫‪66‬‬
‫שים לב !‬
‫קיימות כמה דרכים ש בעזרתן נוכל להוכיח שנקודה מסוימת היא מרכז‬
‫של מעגל החוסם משולש ‪ .‬נדגיש שתיים מהן ‪:‬‬
‫א ‪ .‬נוכיח שהנקודה היא בנקודת המפגש של האנכים האמצעיים במשולש ‪.‬‬
‫ב ‪ .‬נוכיח שהנקודה נמצאת במרחקים שווים משלושת קדקודי המשולש ‪.‬‬
‫תרגילים‬
‫‪.1‬‬
‫‪A‬‬
‫הנקודה ‪ O‬היא מרכז המעגל‬
‫החוסם את המשולש ‪. ABC‬‬
‫נתון ‪. AOB  110 , OAC  28 :‬‬
‫א ‪ .‬חשב את הזווית ‪. BAC‬‬
‫‪O‬‬
‫ב ‪ .‬חשב את הזווית ‪. BOC‬‬
‫תשובה ‪:‬‬
‫‪.2‬‬
‫א ‪ . 63 .‬ב ‪. 126 .‬‬
‫‪B‬‬
‫‪C‬‬
‫הנקודה ‪ O‬היא מרכז המעגל החוסם את המשולש ‪. ABC‬‬
‫נתון ‪. ABO  32 , ACO  25 :‬‬
‫ב ‪ .‬חשב את הזווית ‪. OBC‬‬
‫א ‪. 57 .‬‬
‫ב ‪. 33 .‬‬
‫‪A‬‬
‫‪.3‬‬
‫‪ B , A‬ו‪ C -‬הן נקודות הנמצאות על מעגל ‪.‬‬
‫ה נקודה ‪ O‬נמצאת בתוך המעגל‬
‫‪O‬‬
‫כך ש‪. AO  BO  CO -‬‬
‫הוכח ‪. BOC  2  BAC :‬‬
‫‪.4‬‬
‫‪B‬‬
‫‪C‬‬
‫במשולש ‪ ABC‬נתון ‪. ACB  60 , ABC  40 :‬‬
‫‪A‬‬
‫הנקודה ‪ M‬נמצאת במרחקים שווים‬
‫מקדקודי המשולש ‪.‬‬
‫א ‪ .‬חשב את הזווית ‪. AMB‬‬
‫‪M‬‬
‫ב ‪ .‬חשב את הזווית ‪. BMC‬‬
‫א ‪. 120 .‬‬
‫‪B‬‬
‫ב ‪. 160 .‬‬
‫‪67‬‬
‫‪C‬‬
‫‪.5‬‬
‫‪A‬‬
‫הנקודה ‪ M‬נמצאת בתוך משולש ‪. ABC‬‬
‫נתון ‪. AM  BM  CM :‬‬
‫א ‪ .‬הוכח ‪. BMC  2  BAC :‬‬
‫ב ‪ .‬הוכח ‪. BAM  ACB  90 :‬‬
‫‪M‬‬
‫‪B‬‬
‫‪C‬‬
‫‪.6‬‬
‫המשולש ‪ ABC‬הוא משולש שוו ה שוקיים‬
‫‪A‬‬
‫)‪ (AB  AC‬החסום במעגל ‪.‬‬
‫‪ AD‬הוא הגובה לבסיס ‪. BC‬‬
‫נקודה ‪ O‬נמצאת על הקטע ‪AD‬‬
‫כך ש‪. AO  BO -‬‬
‫הוכח שנקודה ‪ O‬היא מרכז המעגל ‪.‬‬
‫‪.7‬‬
‫‪O‬‬
‫‪C‬‬
‫‪B‬‬
‫‪D‬‬
‫המשולש ‪ ABC‬הוא משולש שווה שוקיים‬
‫‪A‬‬
‫‪ AD‬הוא הגובה לבסיס ‪. BC‬‬
‫נקודה ‪ O‬נמ צאת על הקטע ‪AD‬‬
‫כך ש‪. AO  CO -‬‬
‫א ‪ .‬הוכח שנקודה ‪ O‬היא מרכז המעגל ‪.‬‬
‫ב ‪ .‬הוכח ‪. ACB  ACO  90 :‬‬
‫‪.8‬‬
‫‪O‬‬
‫‪C‬‬
‫‪B‬‬
‫‪D‬‬
‫‪A‬‬
‫‪ B , A‬ו‪ C -‬הן נקודות על מעגל ‪.‬‬
‫‪ D‬ו‪ E -‬הן אמצעי המיתרים ‪ AB‬ו‪. AC -‬‬
‫‪E‬‬
‫נתון ‪. OE  AC , OD  AB :‬‬
‫‪D‬‬
‫‪O‬‬
‫א ‪ .‬הסבר מדוע נקודה ‪ O‬היא מרכז‬
‫‪C‬‬
‫המעגל החוסם את המשולש ‪. ABC‬‬
‫‪B‬‬
‫ב ‪ .‬הוכח ‪. AOC  2  ABC :‬‬
‫‪.9‬‬
‫הנקודה ‪ O‬היא נקודת מפגש האנכים‬
‫‪A‬‬
‫האמצעיים במשולש ‪. ABC‬‬
‫נתון ‪. BOC  120 , AOB  114 :‬‬
‫א ‪ .‬חשב את הזווית ‪. ABC‬‬
‫‪O‬‬
‫ב ‪ .‬חשב את הזווית ‪. BAC‬‬
‫‪B‬‬
‫א ‪ . 63 .‬ב ‪. 60 .‬‬
‫‪68‬‬
‫‪C‬‬
‫‪A‬‬
‫‪. 10‬‬
‫במשולש ‪ , ABC‬הקטעים ‪ OD‬ו‪OE -‬‬
‫הם אנכים אמצעיים לצלעות ‪ BC‬ו‪. AB -‬‬
‫א ‪ .‬הוכח ‪. OA  OB :‬‬
‫ב ‪ .‬הוכח ‪ :‬האנך מ‪ O -‬לצלע ‪AC‬‬
‫חוצה את הצלע ‪. AC‬‬
‫‪. 11‬‬
‫‪D‬‬
‫‪O‬‬
‫‪C‬‬
‫‪B‬‬
‫‪E‬‬
‫‪A‬‬
‫המשולש ‪ ABC‬הוא משולש שווה שוקיים‬
‫‪ AD‬הוא גובה לבסיס ‪. BC‬‬
‫‪E‬‬
‫‪ O‬היא נקודה על הקטע ‪. AD‬‬
‫‪O‬‬
‫נתון ‪. OE  AC , AE  CE :‬‬
‫הוכח שנקודה ‪ O‬היא מרכז המעגל ‪.‬‬
‫‪. 12‬‬
‫‪C‬‬
‫‪B‬‬
‫‪D‬‬
‫‪A‬‬
‫‪ AD‬הוא גובה לבסיס ‪ BC‬במשולש‬
‫שווה‪ -‬שוקיים ‪. (AB  AC) ABC‬‬
‫‪ E‬היא נקודה על ‪ AD‬כך שהמרובע ‪AEBF‬‬
‫הוא דלתון )‪. (AF  BF , AE  BE‬‬
‫הוכח ‪ :‬הנקודה ‪ E‬היא מרכז המעגל‬
‫‪. 13‬‬
‫‪F‬‬
‫‪G‬‬
‫‪E‬‬
‫‪D‬‬
‫‪C‬‬
‫‪B‬‬
‫המשולש ‪ ABC‬הוא שווה‪ -‬צלעות ‪ G .‬היא נקודת מפגש התיכונים במשולש ‪.‬‬
‫הוכח ‪ :‬הנקודה ‪ G‬היא מרכז המעגל החוסם את המשולש ‪. ABC‬‬
‫‪. 14‬‬
‫המשולש ‪ ABC‬הוא ישר‪ -‬זווית ) ‪. (ABC  90‬‬
‫‪C‬‬
‫‪ D‬היא נקודה על היתר ‪. BC‬‬
‫נתון ‪. BDC  112 , C  34 :‬‬
‫‪B‬‬
‫א ‪ .‬הוכח ‪. AD  CD :‬‬
‫‪D‬‬
‫ב ‪ .‬הוכח ‪ :‬הנקודה ‪ D‬היא מרכז המעגל‬
‫‪A‬‬
‫‪69‬‬
‫‪. 15‬‬
‫המשולש ‪ ABC‬הוא משולש ישר‪ -‬זווית‬
‫‪A‬‬
‫)‪ (AB  BC‬החסום במעגל ‪ O .‬היא‬
‫נקודה על היתר ‪ . AC‬נתון ‪. AO  BO :‬‬
‫‪O‬‬
‫הוכח ‪ :‬הנקודה ‪ O‬היא מרכז המעגל‬
‫‪C‬‬
‫‪B‬‬
‫‪C‬‬
‫‪. 16‬‬
‫‪ AB‬הוא מיתר במעגל ‪ .‬הנקודות ‪ C‬ו‪D -‬‬
‫נמצאות על היקף המעגל כך ש‪CD -‬‬
‫חוצה את המיתר ‪ AB‬ומאונך לו ‪.‬‬
‫א ‪ .‬הוכח ‪ CD :‬הוא קוטר במעגל ‪.‬‬
‫ב ‪ O .‬היא נקודה על ‪ CD‬כך ש‪. OC  OB -‬‬
‫הוכח ‪ – O :‬מרכז המעגל ‪.‬‬
‫‪. 17‬‬
‫המיתרים ‪ AB‬ו‪ CD -‬מאונכים זה לזה‬
‫‪A‬‬
‫‪B‬‬
‫‪D‬‬
‫‪C‬‬
‫ונפגשים בנקודה ‪ - O . E‬אמצע ‪. AB‬‬
‫נקודה ‪ F‬נמצאת על הקטע ‪. BE‬‬
‫נתון ‪. CFE  DFE :‬‬
‫‪B‬‬
‫‪O‬‬
‫‪F‬‬
‫‪E‬‬
‫הוכח ‪ :‬הנקו דה ‪ O‬היא מרכז המעגל ‪.‬‬
‫‪D‬‬
‫‪. 18‬‬
‫הנקודות ‪ B , A‬ו‪ C -‬נמצאות על מעגל ‪.‬‬
‫‪A‬‬
‫נקודה ‪ E‬נמצאת על הקוטר ‪AB‬‬
‫ונקודה ‪ D‬נמצאת על המיתר ‪. BC‬‬
‫נתון ‪. ED  BC , BD  DC :‬‬
‫הוכח ‪ :‬הנקודה ‪ E‬היא מרכז המעגל ‪.‬‬
‫‪E‬‬
‫‪D‬‬
‫‪C‬‬
‫‪70‬‬
‫‪B‬‬
‫‪A‬‬
‫‪. 19‬‬
‫‪A‬‬
‫המיתרים ‪ AB‬ו‪ CD -‬של מעגל נחתכים‬
‫‪C‬‬
‫בנקודה ‪ F‬ומאונכים זה לזה ‪.‬‬
‫‪D‬‬
‫‪F‬‬
‫‪ E‬נקודה על הקשת ‪ ) BD‬ראה ציור (‪.‬‬
‫נתון ‪. ABE  ABC  DCE :‬‬
‫‪E‬‬
‫הוכח ‪ AB :‬הוא קוטר במעגל ‪.‬‬
‫‪B‬‬
‫‪. 20‬‬
‫הוכ ח את המשפט ‪ :‬נקודת מפגש האנכים האמצעיים במשולש‬
‫היא מרכז המעגל החוסם את המשולש ‪.‬‬
‫מעגל החסום במשולש‬
‫מעגל החסום במשולש הוא מעגל ששלוש צלעותיו של המשולש‬
‫משיקות לו ‪.‬‬
‫קיים משפט ש לפיו בכל משולש אפשר לחסום מעגל ‪.‬‬
‫‪A‬‬
‫במילים אחרות ‪ ,‬אם נתון משולש ‪, ABC‬‬
‫אז קיים תמיד מעגל המשיק‬
‫לשלוש צלעותיו של המשולש ‪.‬‬
‫מעגל זה נקרא המעגל החסום במשולש ‪.‬‬
‫‪C‬‬
‫‪B‬‬
‫) ‪ ( 1‬כאשר המעגל‬
‫חסום‬
‫במשולש ‪ ,‬ניתן לומר שהמשולש‬
‫חוסם‬
‫את המעגל ‪.‬‬
‫) ‪ ( 2‬לכל משולש קיים רק מעגל אחד החסום בו ‪.‬‬
‫) ‪ ( 3‬מרכז המעגל החסום במשולש נמצא תמיד בתוך המשולש ‪.‬‬
‫משפט ‪ :‬נקודת מפגש חוצי הזוויות במשולש היא מרכז המעגל החסום‬
‫במשולש ‪.‬‬
‫‪A‬‬
‫אם ‪ BE , AD‬ו‪ CF -‬הם חוצי הזוויות‬
‫‪E‬‬
‫במשולש ‪ , ABC‬אז נקודת החיתוך שלהם‬
‫‪F‬‬
‫היא מרכז המעגל החסו ם במשולש ‪. ABC‬‬
‫‪O‬‬
‫‪C‬‬
‫‪71‬‬
‫‪D‬‬
‫‪B‬‬
‫אם‬
‫נתון‬
‫כי הנקודה ‪ O‬היא מרכז‬
‫‪A‬‬
‫המעגל החסום במשולש ‪ , ABC‬אזי ‪:‬‬
‫‪F‬‬
‫) ‪ BO , AO ( 1‬ו‪ CO -‬הם חוצי זוויות המשולש ‪.‬‬
‫‪E‬‬
‫) ‪ ( 2‬מרחקה של הנקודה ‪ O‬מכל אחת‬
‫מצלעות המשולש שווה לרדיוס המעגל‬
‫)‪. (OD  OE  OF  r‬‬
‫הערה ‪:‬‬
‫‪O‬‬
‫‪C‬‬
‫‪B‬‬
‫‪D‬‬
‫במשולש שווה צלעות מרכז המעגל החוסם ומרכז המעגל החסום‬
‫נמצאים באותה נקודה ‪ .‬במשולש שאינו שווה צלעות מרכ ז המעגל החוסם‬
‫ומרכז המעגל החסום לא נמצאים באותה נקודה ‪.‬‬
‫שים לב !‬
‫קיימות כמה דרכים ש בעזרתן נוכל להוכיח שנקודה מסוימת‬
‫היא מרכז של מעגל החסום במשולש ‪ .‬נדגיש שתיים מהן ‪:‬‬
‫א ‪ .‬נוכיח שהנקודה היא נקודת המפגש של חוצי הזוויות במשולש ‪.‬‬
‫ב ‪ .‬נוכיח שהנקודה נמצאת במרחקים שוו ים משלוש צלעות המשולש ‪.‬‬
‫‪. 21‬‬
‫‪A‬‬
‫בתוך משולש ‪ ABC‬חסום מעגל שמרכזו‬
‫בנקודה ‪ . O‬נתון ‪. BAC  72 , ABC  64 :‬‬
‫א ‪ .‬חשב את הזווית ‪. ABO‬‬
‫ב ‪ .‬חשב את הזווית ‪. AOB‬‬
‫‪. 22‬‬
‫א ‪. 32 .‬‬
‫‪O‬‬
‫ב ‪. 112 .‬‬
‫‪C‬‬
‫‪B‬‬
‫‪A‬‬
‫הנקודה ‪ O‬היא מרכז המעגל החסום במשולש ‪. ABC‬‬
‫‪‬‬
‫‪‬‬
‫נתון ‪. ACO  20 , ABC  68 :‬‬
‫א ‪ .‬חשב את הזווית ‪. BAO‬‬
‫‪O‬‬
‫ב ‪ .‬חשב את הזווית ‪. AOC‬‬
‫‪. 23‬‬
‫‪B‬‬
‫‪C‬‬
‫א ‪ . 36 .‬ב ‪. 124 .‬‬
‫‪A‬‬
‫המשולש ‪ ABC‬הוא שווה‪ -‬שוקיים )‪. (AB  AC‬‬
‫בתוך המשולש חסום מעגל‬
‫שמרכזו בנקודה ‪. O‬‬
‫הוכח ‪. OB  OC :‬‬
‫‪O‬‬
‫‪C‬‬
‫‪72‬‬
‫‪B‬‬
‫‪. 24‬‬
‫מעגל שמרכזו ‪ O‬חסום במשולש ‪ . ABC‬המשך‬
‫‪A‬‬
‫הקטע ‪ AO‬חותך את הצלע ‪ BC‬בנקודה ‪. E‬‬
‫נתון ‪. BAC  72 , ABC  68 :‬‬
‫א ‪ .‬חשב את הזווית ‪. BOE‬‬
‫‪O‬‬
‫ב ‪ .‬חשב את הזווית ‪. COE‬‬
‫‪. 25‬‬
‫א ‪ . 70 .‬ב ‪. 56 .‬‬
‫‪C‬‬
‫‪B‬‬
‫‪E‬‬
‫‪A‬‬
‫הנקודה ‪ O‬היא מרכז המעגל החסום‬
‫בתוך משולש ‪ . ABC‬נתון ‪. ACB  56 :‬‬
‫א ‪ .‬חשב את הזווית ‪. AOB‬‬
‫ב ‪ .‬הוכח ‪ :‬מרחקה של הנקודה ‪O‬‬
‫מהצלע ‪ AC‬שווה למרחקה מהצלע ‪. AB‬‬
‫‪. 26‬‬
‫‪O‬‬
‫‪B‬‬
‫‪C‬‬
‫א ‪. 118 .‬‬
‫‪A‬‬
‫המשולש ‪ ABC‬הוא ישר‪ -‬זווית )‪. (AC  BC‬‬
‫הנקו דה ‪ O‬היא מרכז המעגל‬
‫החסום בתוך המשולש ‪.‬‬
‫‪O‬‬
‫הוכח ‪. AOB  135 :‬‬
‫‪B‬‬
‫‪C‬‬
‫‪A‬‬
‫‪. 27‬‬
‫‪ AD‬הוא גובה לצלע ‪ BC‬במשולש ‪. ABC‬‬
‫נקודה ‪ O‬היא מ רכז המעגל‬
‫החסום בתוך המשולש ‪. ABC‬‬
‫‪O‬‬
‫הוכח ‪. AB  AC :‬‬
‫‪C‬‬
‫‪B‬‬
‫‪D‬‬
‫‪A‬‬
‫‪. 28‬‬
‫‪ AD‬הוא תיכון לבסיס ‪. BC‬‬
‫נתון ‪. EF  CF , EF  BC :‬‬
‫הוכח ‪ :‬הנקודה ‪ O‬היא מרכז‬
‫‪F‬‬
‫המעגל החסום בתוך המשולש ‪. ABC‬‬
‫‪C‬‬
‫‪73‬‬
‫‪O‬‬
‫‪D‬‬
‫‪E‬‬
‫‪B‬‬
‫‪. 29‬‬
‫‪A‬‬
‫הנקודה ‪ O‬היא מרכז המעגל החסום‬
‫‪‬‬
‫במשולש ‪ . ABC‬נתון ‪, AOB  114 :‬‬
‫‪ . BOC  124‬חשב את זוויותיו‬
‫‪O‬‬
‫של משולש ‪. ABC‬‬
‫‪B‬‬
‫‪C‬‬
‫‪. 48 , 64 , 68‬‬
‫‪A‬‬
‫‪. 30‬‬
‫המשולש ‪ ABC‬חוסם מעגל ‪.‬‬
‫נקודות ההשקה הן ‪ E , D‬ו‪. F -‬‬
‫נתון ‪. BF  CF :‬‬
‫‪E‬‬
‫‪D‬‬
‫א ‪ .‬הוכח ‪ :‬המשולש ‪ ABC‬הוא שווה‪ -‬שוקיים ‪.‬‬
‫ב ‪ .‬הוכח ‪. AF  DE :‬‬
‫‪C‬‬
‫‪. 31‬‬
‫‪F‬‬
‫המשולש ‪ ABC‬חוסם מעגל ‪.‬‬
‫‪B‬‬
‫‪A‬‬
‫נקודת ההשקה הן ‪ E , D‬ו‪. F -‬‬
‫היקף המשולש ‪ ABC‬הוא ‪ 17‬ס " מ ‪.‬‬
‫נתון ‪ 5 :‬ס " מ ‪. AB ‬‬
‫‪E‬‬
‫‪D‬‬
‫חשב את אורך הקטע ‪. CF‬‬
‫‪. 32‬‬
‫‪C‬‬
‫‪ 3.5‬ס " מ ‪.‬‬
‫‪B‬‬
‫‪F‬‬
‫‪A‬‬
‫משולש חד‪ -‬זווית ‪ ABC‬חוסם מעגל ‪.‬‬
‫‪ E , D‬ו‪ F -‬הן נקודות ההשקה ‪.‬‬
‫‪D‬‬
‫נתון ‪. FEB   , EFD   :‬‬
‫הבע באמצעות ‪ ‬ו‪  -‬את זוויות‬
‫‪F‬‬
‫המשולש ‪. ABC‬‬
‫‪. 33‬‬
‫‪. 180  2 , 180  2 , 2  2  180‬‬
‫‪C‬‬
‫‪E‬‬
‫‪A‬‬
‫במעגל שמרכזו בנקודה ‪ O‬נתון ‪:‬‬
‫הרדיוס ‪ OD‬מאונך למיתר ‪AB‬‬
‫והרדיוס ‪ OE‬מאונך למיתר ‪. BC‬‬
‫הוכח ‪ :‬הנקודה ‪ F‬היא מרכז המעגל‬
‫החסום בתוך המשולש ‪. ABC‬‬
‫‪F‬‬
‫‪D‬‬
‫‪O‬‬
‫‪B‬‬
‫‪C‬‬
‫‪E‬‬
‫‪74‬‬
‫‪B‬‬
‫‪. 34‬‬
‫במשולש ‪ ABC‬נתון ‪. BAC  74 , ABC  72 :‬‬
‫‪A‬‬
‫‪ D‬היא מרכז המעגל החוסם את המשולש ‪.‬‬
‫‪ E‬היא מרכז המעגל החסום‬
‫‪E‬‬
‫בתוך המשולש ‪.‬‬
‫‪D‬‬
‫חשב את הזווית ‪. DAE‬‬
‫‪C‬‬
‫‪B‬‬
‫‪. 19‬‬
‫‪A‬‬
‫‪. 35‬‬
‫הנקודה ‪ D‬היא מרכז המעגל החסום‬
‫במשולש ‪ ABC‬והנקודה ‪ E‬היא מרכז‬
‫המעגל החוסם את המשולש ‪. ABC‬‬
‫‪E‬‬
‫הוכח ‪. AEC  4  ABD :‬‬
‫‪D‬‬
‫‪B‬‬
‫‪C‬‬
‫‪. 36‬‬
‫‪ ABC‬הוא משולש חד‪ -‬זווית שווה‪ -‬שוק יים )‪ AD . (AB  AC‬הוא הגובה‬
‫לבסיס ‪ . BC‬נקודה ‪ E‬היא מרכז המעגל החוסם את המשולש ונקודה ‪F‬‬
‫היא מרכז המעגל החסום במשולש ‪.‬‬
‫הסבר מדוע הנקודות ‪ E‬ו‪ F -‬נמצאות על הקטע ‪. AD‬‬
‫‪. 37‬‬
‫הוכח את המשפט ‪ :‬מרכז המעגל החסום בתוך משולש הוא נקודת‬
‫המפגש של חוצי הזוויות במשולש ‪.‬‬
‫מרובע החסום במעגל‬
‫מרובע החסום במעגל הוא מרובע שכל ארבעת קדקו דיו נמצאים על‬
‫המעגל ‪ .‬מרובע כזה נקרא מרובע בר‪ -‬חסימה במעגל ‪.‬‬
‫משפט ‪ :‬במרובע החסום במעגל סכום כל שתי זוויות נגדיות שווה‬
‫ל‪. 180 -‬‬
‫אם המרובע ‪ ABCD‬חסום במעגל ‪,‬‬
‫‪B‬‬
‫‪A‬‬
‫אזי מתקיים ‪, A  C  180 :‬‬
‫‪D‬‬
‫‪. B  D  180‬‬
‫‪C‬‬
‫משפט ‪ :‬אם במרובע יש זוג אחד של זוויות נגדיות שסכומן ‪ , 180‬אז‬
‫ניתן לחסום את המרובע במעגל ‪ ,‬כלומר המרובע הוא בר חסימה‬
‫במעגל ‪.‬‬
‫ממשפט זה נובע שלא כל מרובע אפשר לחסום במעגל ‪.‬‬
‫‪75‬‬
‫‪.1‬‬
‫חשב את הזוויות ‪ ‬ו‪  -‬בכל אחד מהציורים הבאים ‪:‬‬
‫א‪.‬‬
‫‪‬‬
‫‪‬‬
‫‪.2‬‬
‫ב‪.‬‬
‫‪120‬‬
‫‪‬‬
‫‪108‬‬
‫‪75‬‬
‫‪70‬‬
‫‪2   10‬‬
‫א ‪.   60 ,   110 .‬‬
‫ב ‪.   36 ,   95 .‬‬
‫המרובע ‪ ABCD‬חסום במעגל ‪.‬‬
‫‪‬‬
‫‪B‬‬
‫‪‬‬
‫נתון ‪. ABD  36 , ADB  40 :‬‬
‫‪A‬‬
‫א ‪ .‬חשב את הזווית ‪. BCD‬‬
‫ב ‪ .‬נתון גם ‪. ABC  75 :‬‬
‫חשב את הזווית ‪. BDC‬‬
‫‪.3‬‬
‫א ‪. 76 .‬‬
‫‪C‬‬
‫ב ‪. 65 .‬‬
‫‪A‬‬
‫המשכי המיתרים ‪ AB‬ו‪CD -‬‬
‫‪B‬‬
‫נפגשים בנקודה ‪ ) E‬ראה ציור (‪.‬‬
‫א ‪ .‬הוכח ‪. BAD  BCE :‬‬
‫‪E‬‬
‫ב ‪ .‬הוכח ‪. ADC  CBE :‬‬
‫‪.4‬‬
‫‪D‬‬
‫‪C‬‬
‫המרובע ‪ ABCD‬חסום במעגל שמרכזו ‪O‬‬
‫כך שהצלע ‪ AB‬היא קוטר במעגל ‪.‬‬
‫נתון ‪. DAB  77 , ABC  56 :‬‬
‫א ‪ .‬חשב את הזווית ‪. DCA‬‬
‫ב ‪ .‬חשב את הזווית ‪. DOB‬‬
‫א ‪. 13 .‬‬
‫‪D‬‬
‫‪C‬‬
‫‪B‬‬
‫‪D‬‬
‫‪A‬‬
‫‪O‬‬
‫ב ‪. 154 .‬‬
‫‪E‬‬
‫‪.5‬‬
‫המרובע ‪ ABCD‬חסום במעגל ‪ .‬המשכי‬
‫הצלעות ‪ AB‬ו‪ DC -‬נחתכים בנקודה ‪. E‬‬
‫המשכי הצלעות ‪ BC‬ו‪ AD -‬נחתכים‬
‫‪C‬‬
‫‪F‬‬
‫‪B‬‬
‫בנקודה ‪ . F‬נתון ‪. F  34 , A  58 :‬‬
‫‪D‬‬
‫חשב את הזווית ‪. E‬‬
‫‪A‬‬
‫‪76‬‬
‫‪.6‬‬
‫‪. 30‬‬
‫הנקודה ‪ E‬נמצאת על הקשת ‪. DC‬‬
‫‪B‬‬
‫המשכי המיתרים ‪ AD‬ו‪CE -‬‬
‫נפגשים בנקודה ‪ . F‬נתון ‪. AB  CF :‬‬
‫א ‪ .‬הוכח ‪. AFC  BCD :‬‬
‫ב ‪ .‬נתון ‪. DCF  21 , BAD  115 :‬‬
‫חשב את הזווית ‪. ABC‬‬
‫‪.7‬‬
‫‪D‬‬
‫‪C‬‬
‫‪F‬‬
‫‪E‬‬
‫ב ‪. 94 .‬‬
‫‪A‬‬
‫המשכי המיתרים ‪ AD‬ו‪BC -‬‬
‫נפגשים בנקודה ‪. E‬‬
‫נתון ‪. ACE  ADC :‬‬
‫‪.8‬‬
‫‪A‬‬
‫‪D‬‬
‫‪B‬‬
‫‪E‬‬
‫‪C‬‬
‫א ‪ .‬הוכח ‪. D  BAC  BCA :‬‬
‫ב ‪ .‬הוכח ‪ :‬אם ‪ B  2  DAC‬אז ‪. AD  CD‬‬
‫‪A‬‬
‫‪.9‬‬
‫האלכסון ‪ AC‬חוצה את הזווי ת‬
‫‪ BAD‬ו את הזווית ‪. BCD‬‬
‫הוכח ‪ AC :‬הוא קוטר במעגל ‪.‬‬
‫‪B‬‬
‫‪D‬‬
‫‪C‬‬
‫‪. 10‬‬
‫‪B‬‬
‫המרובע ‪ ABCD‬הוא טרפז )‪(AB  DC‬‬
‫‪A‬‬
‫ה חסום במעגל ‪.‬‬
‫הוכח ‪ ABCD :‬הוא טרפז‬
‫שווה‪ -‬שוקיים ‪.‬‬
‫‪C‬‬
‫‪77‬‬
‫‪D‬‬
‫‪. 11‬‬
‫‪A‬‬
‫‪B‬‬
‫החסום במעגל ‪.‬‬
‫נתון ‪. DAC  66 , BCD  74 :‬‬
‫ב ‪ .‬הוכ ח ‪. AD  AB :‬‬
‫‪. 12‬‬
‫‪C‬‬
‫‪D‬‬
‫א ‪. 40 .‬‬
‫‪A‬‬
‫‪B‬‬
‫במעגל שמרכזו ‪ O‬חסום טרפז ‪. ABCD‬‬
‫‪ , DC‬בסיסו הגדול של הטרפז ‪ ,‬הוא קוט ר‬
‫המעגל ‪ .‬נתון ‪. ADC  62 :‬‬
‫‪C‬‬
‫חשב את הזווית ‪. AOB‬‬
‫‪. 13‬‬
‫‪D‬‬
‫‪O‬‬
‫‪. 68‬‬
‫‪C‬‬
‫מעגל חוסם טרפז ‪. (AB  DC) ABCD‬‬
‫אלכסון הטרפז יוצר עם שוקי הט רפז‬
‫‪D‬‬
‫‪75‬‬
‫את הזוויות ‪ 75‬ו‪ ) 25 -‬ראה ציור (‪.‬‬
‫‪‬‬
‫‪25‬‬
‫חשב את הזווית ‪. BAC‬‬
‫‪B‬‬
‫‪. 40‬‬
‫‪A‬‬
‫‪A‬‬
‫‪. 14‬‬
‫המשכי המיתרים ‪ BD‬ו‪CE -‬‬
‫נחתכים בנק ודה ‪. A‬‬
‫נתון ‪. DE  BC :‬‬
‫הוכח ‪. AD  AE :‬‬
‫‪. 15‬‬
‫החסום במעגל ‪ E .‬היא נקודת‬
‫האמצע של הקשת ‪. DC‬‬
‫א ‪ .‬הוכח ‪. AE  BE :‬‬
‫ב ‪ .‬הוכח ‪. DF  CG :‬‬
‫‪D‬‬
‫‪E‬‬
‫‪B‬‬
‫‪C‬‬
‫‪A‬‬
‫‪B‬‬
‫‪C‬‬
‫‪F‬‬
‫‪G‬‬
‫‪E‬‬
‫‪78‬‬
‫‪D‬‬
‫‪. 16‬‬
‫המרובע ‪ ABCD‬חסום במעגל שמרכזו ‪, O‬‬
‫‪B‬‬
‫‪C‬‬
‫כך שהצלע ‪ AD‬עוברת דרך מרכז המעגל ‪.‬‬
‫הרדיוס ‪ OC‬חוצה את הזווית ‪. BCD‬‬
‫‪D‬‬
‫‪  DC‬‬
‫א ‪ .‬הוכח ‪ :‬‬
‫‪. BC‬‬
‫‪A‬‬
‫‪O‬‬
‫ב ‪ .‬הוכח ‪. AB  OC :‬‬
‫‪. 17‬‬
‫המרובע ‪ ABCD‬חסום במעגל‬
‫‪B‬‬
‫שמרכזו ‪ . O‬בנקודה ‪ A‬מעבירים‬
‫‪O‬‬
‫משיק למעגל החותך את המשך‬
‫המיתר ‪ CD‬בנקודה ‪. E‬‬
‫‪A‬‬
‫הוכח ‪. BCD  DAE  90 :‬‬
‫‪C‬‬
‫‪E‬‬
‫‪. 18‬‬
‫טרפז ‪ (AB  DC) ABCD‬חסום במעגל‬
‫‪ E‬היא נקודה על המשך הבסיס ‪DC‬‬
‫כך ש‪ BE -‬משיק למעגל ‪.‬‬
‫א ‪ .‬הוכח ‪. ABD  CBE :‬‬
‫ב ‪ .‬הוכח ‪. AB  CE :‬‬
‫‪A‬‬
‫‪B‬‬
‫כך שהבסיס הקט ן ‪ AB‬שווה לשוק ‪. AD‬‬
‫‪. 19‬‬
‫‪D‬‬
‫‪E‬‬
‫‪D‬‬
‫‪C‬‬
‫‪A‬‬
‫בנקודה ‪ C‬מעבירים משיק למעגל‬
‫החותך את המשכי המיתרים‬
‫‪D‬‬
‫‪ AB‬ו‪ AD -‬בנקודות ‪ E‬ו‪. F -‬‬
‫‪B‬‬
‫א ‪ .‬הוכח ‪. EBC  CDF  180 :‬‬
‫ב ‪ .‬הוכח ‪. BAD  BCE  DCF :‬‬
‫‪. 20‬‬
‫‪F‬‬
‫‪C‬‬
‫‪E‬‬
‫הצלע ‪ AB‬של המרובע ‪ ABCD‬החסום במעגל‬
‫היא קוטר באותו מעגל ‪ M .‬מרכז המעגל ‪.‬‬
‫‪79‬‬
‫‪D‬‬
‫‪C‬‬
‫המשכי הצלעות ‪ AD‬ו‪ BC -‬נפגשים בנקודה ‪. E‬‬
‫א ‪ .‬הוכח ‪. MDC  AEB :‬‬
‫ב ‪ .‬הוכח ‪ :‬הישר ‪ MD‬משיק בנקודה ‪D‬‬
‫למעגל החוסם את המ שולש ‪. DCE‬‬
‫‪E‬‬
‫‪B‬‬
‫‪M‬‬
‫‪A‬‬
‫‪. 21‬‬
‫בשרטוטים הבאים נתון מרובע ‪.‬‬
‫קבע האם המרובע ניתן ל חס ימה במעגל ‪.‬‬
‫‪C‬‬
‫א‪.‬‬
‫‪‬‬
‫‪130‬‬
‫‪B‬‬
‫ב‪.‬‬
‫‪D‬‬
‫‪96‬‬
‫‪A‬‬
‫‪‬‬
‫‪B‬‬
‫‪50‬‬
‫‪. 22‬‬
‫‪A‬‬
‫‪C‬‬
‫א ‪ .‬כן ‪.‬‬
‫‪74‬‬
‫‪F‬‬
‫ב ‪ .‬לא ‪.‬‬
‫‪A‬‬
‫‪ AD‬ו‪ BE -‬הם גבהים ב משולש ‪. ABC‬‬
‫‪E‬‬
‫‪ F‬היא נקודת מפגש הגבהים במשולש ‪.‬‬
‫‪F‬‬
‫הוכח ‪ :‬המרובע ‪CDFE‬‬
‫ניתן לחסימה במעגל ‪.‬‬
‫‪C‬‬
‫‪B‬‬
‫‪D‬‬
‫‪A‬‬
‫‪. 23‬‬
‫הנקודות ‪ D‬ו‪ E -‬נמצאות על הצלעות‬
‫‪ AB‬ו‪ AC -‬של משולש ‪ABC‬‬
‫‪E‬‬
‫כך שמתקיים ‪. ADE  ACB‬‬
‫‪D‬‬
‫א ‪ .‬הוכח ‪ :‬המרובע ‪DECB‬‬
‫ב ‪ .‬הוכח ‪. BDC  BEC :‬‬
‫‪. 24‬‬
‫‪C‬‬
‫המשולש ‪ ABC‬הוא ישר‪ -‬זווית ) ‪. (ABC  90‬‬
‫‪B‬‬
‫‪A‬‬
‫מנקודה ‪ , D‬הנמצאת על היתר ‪, AC‬‬
‫מעבירים ל‪ AC -‬אנך החותך את ‪AB‬‬
‫בנקודה ‪ E‬ואת המשך ‪ CB‬בנקודה ‪. F‬‬
‫א ‪ .‬הוכח ‪ :‬המרובע ‪BCDE‬‬
‫‪D‬‬
‫‪E‬‬
‫ב ‪ .‬הוכח ‪. DCE  DBE :‬‬
‫‪. 25‬‬
‫‪C‬‬
‫הנקודות ‪ E‬ו‪ F -‬נמצאות על הצלעות ‪ AB‬ו‪AD -‬‬
‫של מלבן ‪ . ABCD‬נתון ‪. AE  BC , AF  BE :‬‬
‫א ‪ .‬הוכח ‪. AEF  BCE :‬‬
‫ב ‪ .‬הוכח ‪ :‬המרובע ‪ DFEC‬ניתן לחסימה במעגל ‪.‬‬
‫ג ‪ .‬הוכח ‪. FCE  FDE :‬‬
‫‪80‬‬
‫‪B‬‬
‫‪B‬‬
‫‪F‬‬
‫‪E‬‬
‫‪A‬‬
‫‪F‬‬
‫‪C‬‬
‫‪D‬‬
‫‪. 26‬‬
‫המשולש ‪ ABC‬הוא ישר‪ -‬זווית )‪. (AB  BC‬‬
‫‪A‬‬
‫‪ AC‬ו‪ AB -‬בהתאמה כך ש‪. AC  DE -‬‬
‫‪D‬‬
‫א ‪ .‬הוכח ‪ :‬המרובע ‪DCBE‬‬
‫‪E‬‬
‫ב ‪ .‬נתון ‪ 8 :‬ס " מ ‪. CE ‬‬
‫חשב את הרדיוס של המעגל שבסעיף א ' ‪.‬‬
‫‪. 27‬‬
‫‪C‬‬
‫‪B‬‬
‫ב‪ 4 .‬ס"מ‪.‬‬
‫הנקודות ‪ E‬ו‪ F -‬נמצאות על הצלעות ‪BC‬‬
‫ו‪ DC -‬של ריבוע ‪ . ABCD‬נתון ‪. BE  CF :‬‬
‫א ‪ .‬הוכח ‪ :‬המרובע ‪AGFD‬‬
‫‪A‬‬
‫‪B‬‬
‫‪G‬‬
‫‪E‬‬
‫בר‪ -‬חסימה במעגל ‪.‬‬
‫ב ‪ .‬נקודה ‪ M‬היא אמצע הקטע ‪. AF‬‬
‫הוכח ‪. AMD  2AGD :‬‬
‫‪. 28‬‬
‫‪C‬‬
‫‪F‬‬
‫‪D‬‬
‫המשולשים ‪ ABC‬ו‪ AMN -‬הם ישרי‪ -‬זווית‬
‫‪N‬‬
‫ושווי‪ -‬שוקיים )‪. (AB  AC , AM  AN‬‬
‫א ‪ .‬הוכח ‪. BMA  CNA :‬‬
‫ב ‪ .‬המשך הצלע ‪ BM‬חותך את הצלע ‪CN‬‬
‫בנקודה ‪ . P‬הוכח ‪ :‬המרובע ‪AMPN‬‬
‫הוא בר‪ -‬חסימה במעגל ‪.‬‬
‫‪A‬‬
‫‪P‬‬
‫‪M‬‬
‫‪C‬‬
‫‪B‬‬
‫ג ‪ .‬הוכח ‪. BP  CN :‬‬
‫‪A‬‬
‫‪. 29‬‬
‫המשולשים ‪ ABC‬ו‪ CDE -‬הם שווי‪ -‬צלעות ‪.‬‬
‫א ‪ .‬הוכח ‪. ACE  BCD :‬‬
‫ב ‪ .‬הי שר ‪ AE‬חותך את הקטע ‪BD‬‬
‫בנקודה ‪ . H‬הוכח ‪. AHB  60 :‬‬
‫‪E‬‬
‫‪C‬‬
‫ג ‪ .‬הוכח כי המרובע ‪EHDC‬‬
‫הוא בר חסימה במעגל ‪.‬‬
‫‪H‬‬
‫‪D‬‬
‫‪81‬‬
‫‪B‬‬
‫‪. 30‬‬
‫המשולש ‪ ABC‬הוא שווה‪ -‬צלעות ‪.‬‬
‫‪A‬‬
‫‪ BC‬ו‪ AC -‬כך ש‪. AC  DC  BC  AE -‬‬
‫א ‪ .‬חשב את הזווית ‪. DFE‬‬
‫‪E‬‬
‫ב ‪ .‬הוכח שהמרובע ‪CDFE‬‬
‫‪F‬‬
‫בר‪ -‬חסימה במעגל ‪.‬‬
‫‪. 31‬‬
‫‪D‬‬
‫‪C‬‬
‫ג ‪ .‬הוכח ‪. DFC  DEC :‬‬
‫‪B‬‬
‫א ‪. 120 .‬‬
‫‪B‬‬
‫במרובע ‪ ABCD‬העבירו ארבעה חוצי‪ -‬זווית ‪:‬‬
‫‪A‬‬
‫‪G‬‬
‫‪. DF , CH , BH , AF‬‬
‫‪H‬‬
‫א ‪ .‬הוכח ‪ :‬המעגל העובר דרך הנקודות‬
‫‪F‬‬
‫‪E‬‬
‫‪ F , E‬ו‪ , G -‬עובר גם דרך הנקודה ‪. H‬‬
‫‪C‬‬
‫ב ‪ .‬נתון ‪. EH  GH :‬‬
‫‪D‬‬
‫הוכח ‪. GFH  EFH :‬‬
‫‪. 32‬‬
‫‪A‬‬
‫‪ ABD‬ו‪ BDC -‬הם משולשים‬
‫ישרי‪ -‬זווית בעלי יתר משותף‬
‫) ‪.( BCD  90 , BAD  90‬‬
‫‪D‬‬
‫‪B‬‬
‫הוכח ‪. ABD  ACD :‬‬
‫‪C‬‬
‫‪. 33‬‬
‫‪B‬‬
‫בציור מתואר המרובע ‪. ABCD‬‬
‫‪A‬‬
‫נתון ‪. DAC  DBC :‬‬
‫הוכח ‪ :‬המעגל החוסם את המשולש ‪ADC‬‬
‫עובר גם דרך ה נקודה ‪. B‬‬
‫‪D‬‬
‫‪C‬‬
‫‪C‬‬
‫‪. 34‬‬
‫‪ AD‬ו‪ BE -‬הם גבהים במשולש ‪. ABC‬‬
‫א ‪ .‬הוכח ‪ :‬המעגל העובר דרך הנקודות‬
‫‪D‬‬
‫‪ B , A‬ו‪ E -‬עובר גם דרך הנקודה ‪. D‬‬
‫‪E‬‬
‫ב ‪ .‬הנק ודה ‪ O‬היא אמצע הצלע ‪. AB‬‬
‫הוכח ‪. OD  OE :‬‬
‫‪B‬‬
‫‪82‬‬
‫‪A‬‬
‫‪. 35‬‬
‫מנקודה ‪ D‬הנמצאת מחוץ למשולש ‪ABC‬‬
‫מעבירים אנכים ‪ DF , DE‬ו‪DG -‬‬
‫לצלעות ‪ AC , AB‬ו‪ BC -‬בהתאמה ‪.‬‬
‫א ‪ .‬הוכח ‪ :‬המרובע ‪AEDF‬‬
‫‪A‬‬
‫‪F‬‬
‫‪E‬‬
‫‪G‬‬
‫ב ‪ .‬הוכח ‪ :‬המרובע ‪BEGD‬‬
‫‪C‬‬
‫‪B‬‬
‫‪D‬‬
‫‪. 36‬‬
‫הוכח את המשפט ‪ :‬במרובע החסום במעגל סכום כל שתי זוויות‬
‫נגדיות שווה ל‪. 180 -‬‬
‫‪. 37‬‬
‫הוכח את המשפט ‪ :‬אם במרובע יש זוג אחד של זוויות נגדיות שסכומן‬
‫‪ , 180‬אז ניתן לחסום את המרוב ע בתוך מעגל ‪.‬‬
‫מרובע החוסם מעגל‬
‫מרובע ה חוסם מעגל הוא מרובע שכל ארבע צלעותיו משיקות למעגל ‪.‬‬
‫מרובע כזה נקרא גם מרובע משיקים ‪.‬‬
‫משפט ‪ :‬במרובע החוסם מעגל סכום שתי צלעות נגדיות שווה לסכום‬
‫‪B‬‬
‫שתי הצלעות הנגדיות האחרות ‪.‬‬
‫‪A‬‬
‫אם המרובע ‪ ABCD‬חוסם מעגל ‪,‬‬
‫אזי מתקיים ‪. AB  DC  AD  BC :‬‬
‫‪C‬‬
‫‪D‬‬
‫משפט ‪ :‬אם סכום שתי צלעות נגדיות במרובע שווה לסכום שתי הצלעות‬
‫הנגדיות האחרות ‪ ,‬אזי אפשר לחסום במרובע מעגל ‪.‬‬
‫ממשפט זה נובע שלא בכל מרובע אפשר לחסום מעגל ‪.‬‬
‫‪. 38‬‬
‫‪A‬‬
‫המרובע ‪ ABCD‬חוסם מעגל ‪.‬‬
‫‪D‬‬
‫נתון ‪ 7 :‬ס " מ ‪ 8 , AB ‬ס " מ ‪, BC ‬‬
‫‪ 5‬ס " מ ‪. DC ‬‬
‫חשב את אורך הצלע ‪. AD‬‬
‫‪ 4‬ס"מ‪.‬‬
‫‪B‬‬
‫‪83‬‬
‫‪C‬‬
‫‪. 39‬‬
‫‪A‬‬
‫‪B‬‬
‫המרובע ‪ ABCD‬הוא טרפז שווה‪ -‬שוקיים‬
‫)‪ (AD  BC , AB  DC‬החוסם מעגל ‪.‬‬
‫נתון ‪ 6 :‬ס " מ ‪ 10 , AB ‬ס " מ ‪. DC ‬‬
‫חשב את אורך השוק ‪. AD‬‬
‫‪. 40‬‬
‫‪ 8‬ס"מ‪.‬‬
‫‪D‬‬
‫‪C‬‬
‫‪B‬‬
‫נקודות ההשקה הן ‪ G , F , E‬ו‪. H -‬‬
‫‪E‬‬
‫נתון ‪ 7 :‬ס " מ ‪ 4 , AB ‬ס " מ ‪, BE ‬‬
‫‪A‬‬
‫‪F‬‬
‫‪ 9‬ס " מ ‪ 3 , BC ‬ס " מ ‪. DG ‬‬
‫א ‪ .‬חשב את אורך הצלע ‪. DC‬‬
‫‪H‬‬
‫ב ‪ .‬חשב את אורך הצלע ‪. AD‬‬
‫‪. 41‬‬
‫א‪ 8 .‬ס"מ‪.‬‬
‫ב‪ 6 .‬ס"מ‪.‬‬
‫‪C‬‬
‫‪G‬‬
‫‪D‬‬
‫טרפז שווה‪ -‬שוקיים חוס ם מעגל ‪ .‬אורך קטע האמצעים של הטרפז‬
‫הוא ‪ 8‬ס " מ ‪ .‬מהו היקף הטרפז ?‬
‫‪. 42‬‬
‫‪ 32‬ס " מ ‪.‬‬
‫‪A‬‬
‫‪B‬‬
‫המרובע ‪ ABCD‬הוא טרפז שווה‪ -‬שוקיים‬
‫) ‪ ( AD  BC , AB  DC‬החו סם מעגל ‪.‬‬
‫נתון ‪ 12 :‬ס " מ ‪. ADC  60 , AD ‬‬
‫חשב את אורכי הבסיסים ‪ AB‬ו‪. DC -‬‬
‫‪ 6‬ס " מ ‪ 18 ,‬ס " מ ‪.‬‬
‫‪D‬‬
‫‪C‬‬
‫‪A‬‬
‫‪. 43‬‬
‫‪E‬‬
‫נתון ‪, ABC  120 , DAB  100 :‬‬
‫‪. BCD  70‬‬
‫‪B‬‬
‫‪D‬‬
‫חשב את זוויותיו של המרובע ‪. EFGH‬‬
‫‪H‬‬
‫‪F‬‬
‫‪G‬‬
‫‪C‬‬
‫‪. 85 , 70 , 95 , 110‬‬
‫‪84‬‬
‫‪A‬‬
‫‪. 44‬‬
‫המרובע ‪ ABCD‬חוסם מעגל שמרכזו ‪. O‬‬
‫‪‬‬
‫‪‬‬
‫‪B‬‬
‫‪‬‬
‫נתון ‪. ADC  80 , BCD  70 , ABC  120 :‬‬
‫א ‪ .‬חשב את הזווית ‪. BOC‬‬
‫‪O‬‬
‫ב ‪ .‬חשב את הזוית ‪. AOD‬‬
‫‪. 45‬‬
‫א ‪. 85 .‬‬
‫ב ‪. 95 .‬‬
‫‪C‬‬
‫‪D‬‬
‫הוכח ‪ :‬נקודת מפגש האלכסונים של מעוין היא מרכז המעגל החסום‬
‫בתוך המעוין ‪.‬‬
‫‪E‬‬
‫‪B‬‬
‫‪. 46‬‬
‫‪A‬‬
‫לפניך מעגל ה חסום בתוך ריבוע ‪. ABCD‬‬
‫‪H‬‬
‫‪F‬‬
‫הוכח ‪ :‬המרובע ‪ EFGH‬הוא ריבוע ‪.‬‬
‫‪C‬‬
‫‪D‬‬
‫‪G‬‬
‫‪A‬‬
‫‪. 47‬‬
‫המעוין ‪ ABCD‬חוסם מעגל ‪.‬‬
‫‪H‬‬
‫‪E‬‬
‫‪B‬‬
‫הוכח ‪ :‬המרובע ‪EFGH‬‬
‫‪D‬‬
‫הוא מלבן ‪.‬‬
‫‪F‬‬
‫‪G‬‬
‫‪C‬‬
‫‪. 48‬‬
‫‪B‬‬
‫המרובע ‪ ABCD‬חוסם מעגל שמרכזו‬
‫בנקודה ‪. O‬‬
‫א ‪ .‬הוכח ‪. AOB  COD  180 :‬‬
‫‪A‬‬
‫‪O‬‬
‫ב ‪ .‬הוכח ‪. BOC  AOD  180 :‬‬
‫‪C‬‬
‫‪. 49‬‬
‫‪D‬‬
‫טרפז שווה‪ -‬שוקיים ‪(AB  DC) ABCD‬‬
‫‪B‬‬
‫חוסם מעגל ‪.‬‬
‫‪E‬‬
‫‪F‬‬
‫א ‪ .‬הוכח ‪. EF  FG :‬‬
‫‪A‬‬
‫‪H‬‬
‫ב ‪ .‬הוכח ‪ EG :‬הוא קוטר במעגל ‪.‬‬
‫ג ‪ .‬הוכח ‪ :‬המרובע ‪ EFGH‬הוא דלתון ‪.‬‬
‫‪85‬‬
‫‪C‬‬
‫‪G‬‬
‫‪D‬‬
‫‪. 50‬‬
‫א ‪ .‬במרובע ‪ ABCD‬נתון ‪ 9 :‬ס " מ ‪ 8 , AB ‬ס " מ ‪ 6 , BC ‬ס " מ ‪, DC ‬‬
‫‪ 7‬ס " מ ‪ . AD ‬האם ניתן ל חס ום מעגל במרובע ‪? ABCD‬‬
‫ב ‪ .‬ב מרובע ‪ ABCD‬נתון ‪ 6 :‬ס " מ ‪ 5 , AB ‬ס " מ ‪ 8 , BC ‬ס " מ ‪, CD ‬‬
‫‪ 10‬ס " מ ‪ . AD ‬האם ניתן ל חס ום מעגל במרובע ‪? ABCD‬‬
‫א ‪ .‬כן ‪.‬‬
‫ב ‪ .‬לא ‪.‬‬
‫‪B‬‬
‫‪. 51‬‬
‫‪x2‬‬
‫אורכי צלעותיו של מרובע ‪ABCD‬‬
‫רשומים בשרטוט ‪ .‬ידוע כי בתוך‬
‫‪A‬‬
‫‪2x  1‬‬
‫המרובע ניתן לחסום מעגל ‪.‬‬
‫‪x 1‬‬
‫מצא את היקף המרובע ‪.‬‬
‫‪ 30‬ס " מ ‪.‬‬
‫‪. 52‬‬
‫‪C‬‬
‫‪D‬‬
‫‪x3‬‬
‫‪A‬‬
‫‪ BD‬חוצה את הזווית ‪ABC‬‬
‫ו‪ CE -‬חוצה את הזווית ‪. ACB‬‬
‫‪ BD‬ו‪ CE -‬נפגשים בנקודה ‪. F‬‬
‫‪D‬‬
‫א ‪ .‬הוכח ‪. DF  EF :‬‬
‫‪F‬‬
‫‪E‬‬
‫ב ‪ .‬הסבר מדוע אפשר לחסום‬
‫מעגל בתוך המרובע ‪. ADFE‬‬
‫‪. 53‬‬
‫‪B‬‬
‫‪C‬‬
‫‪A‬‬
‫‪ BD‬ו‪ CE -‬הם גבהים לשוקיים במשולש‬
‫שווה‪ -‬שוקיים ‪. (AB  AC) ABC‬‬
‫א ‪ .‬הוכח ‪ :‬אפשר לחסום את המרובע‬
‫‪D‬‬
‫‪ ADFE‬בתוך מעגל ‪.‬‬
‫‪F‬‬
‫‪E‬‬
‫ב ‪ .‬הוכח ‪ :‬אפשר לחסום מעגל‬
‫בתוך המרובע ‪. ADFE‬‬
‫‪. 54‬‬
‫‪B‬‬
‫‪C‬‬
‫קבע ב עבור כל אחד מהמרובעים הבאים אם ניתן לחסום בו מעגל ‪:‬‬
‫א ‪ .‬ריבוע ‪.‬‬
‫ב ‪ .‬דלתון ‪.‬‬
‫א ‪ .‬כן ‪ .‬ב ‪ .‬כן ‪.‬‬
‫ג ‪ .‬מעוין ‪.‬‬
‫ג ‪ .‬כן ‪.‬‬
‫ד ‪ .‬מקבילית ‪.‬‬
‫ה ‪ .‬מלבן ‪.‬‬
‫ד ‪ .‬לא ‪ ,‬אלא אם כן המקבילית היא מעוין ‪.‬‬
‫ה ‪ .‬לא ‪ ,‬אלא אם כן המלבן הוא ריבוע ‪.‬‬
‫‪. 55‬‬
‫הוכח את המשפט ‪ :‬במרובע ה חוסם מעגל סכום זוג אחד של צלעות‬
‫נגדיות שווה לסכום של זוג הצלעות הנגדיות האחרות ‪.‬‬
‫‪. 56‬‬
‫הוכח את המשפט ‪ :‬אם במרובע סכום זוג אחד של צלעות נגדיות שווה‬
‫לסכום של זוג הצלעות הנגדיות האחרות ‪ ,‬אז אפשר לחסום מעגל‬
‫במרובע ‪.‬‬
‫‪86‬‬
‫שני מעגלים‬
‫א ‪ .‬שני מעגלים החותכים זה את זה‬
‫בשתי נקודות‬
‫נקראים מעגלים‬
‫נחתכים ‪ .‬למעגלים נחתכים יש‬
‫מיתר משותף ‪.‬‬
‫ב ‪ .‬שני מעגלים שאינם‬
‫חותכים זה את זה נקראים מעגלים‬
‫זרים ‪.‬‬
‫אם מעגל אחד נמצא מחוץ למעגל‬
‫השני ‪ ,‬המעגלים נקראים מע גלים‬
‫חיצוניים ‪.‬‬
‫אם מעגל אחד נמצא בתוך המעגל‬
‫השני ‪ ,‬המעגלים נקראים מעגלים‬
‫פנימיים ‪.‬‬
‫ג ‪ .‬שני מעגלים שיש להם‬
‫נקודה אחת משותפת נקראים מעגלים‬
‫משיקים ‪.‬‬
‫הנקודה המשותפת נקראת נקודת ההשקה או נקודת המגע ‪.‬‬
‫מעגלים המשיקים מבפנים ‪:‬‬
‫מעגלים המשיקים מב חוץ ‪:‬‬
‫שים לב !‬
‫כאשר שני מעגלים משיקים מבחוץ או מבפנים‬
‫אפשר לבצע בניית עזר על ידי כך שנעביר בנקודת‬
‫ההשקה משיק משותף לשני המעגלים ‪.‬‬
‫א ‪ .‬שני מעגלים בעלי מרכז משותף‬
‫נקראים מעגלים מרכזיים ‪.‬‬
‫ב ‪ .‬שני מעגלים בעלי רדיוסים שווים‬
‫‪87‬‬
‫נקראים מעגלים שווים ‪.‬‬
‫קטע מרכזים‬
‫קטע המחבר את המרכזים של שני מעגלים נקרא קטע מרכזים ‪.‬‬
‫משפט ‪ :‬קטע המרכזים של שני מעגלים נחתכים ‪ ,‬חוצה את המיתר‬
‫המשותף לשני המעגלים ומאונך לו ‪.‬‬
‫‪A‬‬
‫אם המעגלים ‪ M‬ו‪ N -‬נחתכים בנקודות ‪ A‬ו‪B -‬‬
‫כך ש‪ AB -‬הוא המיתר המשותף‬
‫‪N‬‬
‫לשני המעגלים ‪ ,‬אזי ‪AP  BP , MN  AB‬‬
‫‪P‬‬
‫‪M‬‬
‫‪B‬‬
‫) ‪ P‬היא נקודת החי תוך של ‪ MN‬ו‪.( AB -‬‬
‫משפט ‪ :‬קטע המרכזים של שני מעגלים המשיקים זה לזה מבחוץ‬
‫עובר דרך נקודת ההשקה שבין שני המעגלים ‪.‬‬
‫אם המעגלים ‪ M‬ו‪ N -‬משיקים מבחוץ‬
‫בנקודה ‪ , A‬אזי הקטע ‪MN‬‬
‫עובר דרך הנקודה ‪. A‬‬
‫‪N‬‬
‫‪M‬‬
‫‪A‬‬
‫משפט ‪ :‬כאשר שני מעגלים משיקים זה לזה מבפנים ‪ ,‬אז המשכו של‬
‫קטע המרכזים עובר דרך נקודת ההשקה שבין שני המעגלים ‪.‬‬
‫אם המעגלים ‪ M‬ו‪ N -‬משיקים מבפנים‬
‫בנקודה ‪ , A‬אז המשך הקטע ‪MN‬‬
‫עובר דרך הנקודה ‪. A‬‬
‫‪A‬‬
‫‪N‬‬
‫‪M‬‬
‫שים לב !‬
‫א ‪ .‬כאשר שני מעגלים משיקים מבחוץ ‪ ,‬אזי קטע המרכזים שווה‬
‫לסכום הרדיוסים של שני המעגלים ‪.‬‬
‫ב ‪ .‬כאשר שני מעגלים משיקים מבפנים ‪ ,‬אזי קטע המרכזים שווה‬
‫להפרש בין הרדיוס של המעגל הגדול לרדיוס של המעגל הקטן ‪.‬‬
‫‪88‬‬
‫‪.1‬‬
‫בציור מתוארים מעגלים שמרכזיהם‬
‫בנקודות ‪ E‬ו‪ . F -‬נתון ‪ 4 :‬ס " מ ‪, AE ‬‬
‫‪ 2‬ס " מ ‪ 3 , DF ‬ס " מ ‪. BC ‬‬
‫א ‪ .‬חשב את אורך קטע המרכזים )‪. (EF‬‬
‫‪D‬‬
‫‪F‬‬
‫‪C‬‬
‫‪B‬‬
‫‪A‬‬
‫‪E‬‬
‫ב ‪ .‬חשב את אורך הקטע ‪. AD‬‬
‫‪.2‬‬
‫א‪ 9 .‬ס"מ‪.‬‬
‫ב ‪ 15 .‬ס " מ ‪.‬‬
‫בציור מתוארים מעגלים שמרכזיהם‬
‫בנקודות ‪ E‬ו‪. F -‬‬
‫נתון ‪ 18 :‬ס " מ ‪ 4 , AD ‬ס " מ ‪. BC ‬‬
‫‪D‬‬
‫חשב את אורך קטע המרכזים )‪. (EF‬‬
‫‪C‬‬
‫‪F‬‬
‫‪B‬‬
‫‪E‬‬
‫‪A‬‬
‫‪ 8‬ס"מ‪.‬‬
‫‪.3‬‬
‫מעגלים שמרכזיהם בנקודות ‪ M‬ו‪N -‬‬
‫נחתכים בנקודות ‪ C‬ו‪. D -‬‬
‫א ‪ .‬הוכח ‪ :‬המרובע ‪ MDNC‬הוא דלתון ‪.‬‬
‫ב ‪ .‬הוכח ‪ :‬קטע המרכזים ‪ MN‬חוצה את‬
‫המיתר המשותף ‪ CD‬ומאונך לו ‪.‬‬
‫‪D‬‬
‫‪.4‬‬
‫בציור מתוארים שני מעגלים שווים‬
‫‪A‬‬
‫‪C‬‬
‫‪N‬‬
‫‪M‬‬
‫שמרכזיהם בנקודות ‪ M‬ו‪. N -‬‬
‫‪ AB‬הוא מיתר משותף לשני המעגלים ‪.‬‬
‫‪N‬‬
‫‪M‬‬
‫א ‪ .‬הוכח ‪. AM  BN :‬‬
‫‪.5‬‬
‫ב ‪ .‬הוכח ‪. AB  MN :‬‬
‫‪B‬‬
‫נתונים שני מעגלים בעלי מרכז משותף ‪. O‬‬
‫‪B‬‬
‫‪ AC‬הוא קוטר במעגל החיצוני‬
‫‪O‬‬
‫ו‪ BD -‬הוא קוטר במעגל הפנימי ‪.‬‬
‫הוכח ‪ :‬המרובע ‪ ABCD‬הוא מק בילית ‪.‬‬
‫‪89‬‬
‫‪A‬‬
‫‪D‬‬
‫‪C‬‬
‫‪.6‬‬
‫מעגלים שמרכזיהם בנקודות ‪ M‬ו‪N -‬‬
‫נחתכים בנקודות ‪ C‬ו‪ . D -‬הקטע ‪MN‬‬
‫חותך את המעגלים בנקודות ‪ A‬ו‪. B -‬‬
‫נתון ‪. N   , M   :‬‬
‫‪ ‬‬
‫‪. ADB ‬‬
‫א ‪ .‬הוכח ‪:‬‬
‫‪2‬‬
‫ב ‪ .‬נתון ‪ . ADB  32 :‬חשב את הזווית ‪. MDN‬‬
‫‪C‬‬
‫‪N‬‬
‫‪A‬‬
‫‪B‬‬
‫‪M‬‬
‫‪D‬‬
‫ב ‪. 116 .‬‬
‫‪B‬‬
‫‪.7‬‬
‫שני מעגלים נחתכים בנקודות ‪ B‬ו‪. D -‬‬
‫הקטע ‪ ADC‬הוא קו ישר ‪.‬‬
‫נתון ‪ AB :‬הוא קוטר במעגל השמאלי ‪.‬‬
‫הוכח ‪ BC :‬הוא קוטר במעגל הימני ‪.‬‬
‫‪.8‬‬
‫‪C‬‬
‫‪A‬‬
‫‪D‬‬
‫שני מעגלים שווים שמרכזיהם בנקודות‬
‫‪A‬‬
‫‪ M‬ו‪ N -‬נחתכים בנקודות ‪ A‬ו‪ B -‬כך‬
‫שהקטרים ‪ AC‬ו‪ AD -‬מאונכים זה לזה ‪.‬‬
‫א ‪ .‬הוכח שהקטע ‪ CBD‬הוא קו ישר ‪.‬‬
‫ב ‪ .‬חשב את הזווית ‪. BAD‬‬
‫‪D‬‬
‫‪B‬‬
‫ג ‪ .‬הוכח ‪. MN  DC :‬‬
‫‪.9‬‬
‫‪C‬‬
‫ב ‪. 45 .‬‬
‫שני מעגלים בעלי אותו רדיוס נחתכים‬
‫בנקודות ‪ A‬ו‪ . B -‬הקטע ‪ CD‬עובר דרך‬
‫‪A‬‬
‫‪D‬‬
‫‪C‬‬
‫הנקודה ‪ . A‬נתון ‪. AB  CD :‬‬
‫א ‪ .‬הוכח ‪. AC  AD :‬‬
‫ב ‪ .‬הוכח שקטע המרכזים המחבר את מרכזי‬
‫‪B‬‬
‫שני המעגלים שווה למיתר ‪. AD‬‬
‫‪. 10‬‬
‫שני מעגלים בעלי אותו רדיוס נחתכים‬
‫‪D‬‬
‫‪A‬‬
‫בנקודות ‪ A‬ו‪. B -‬‬
‫‪ AC‬הוא קוטר במעגל אחד ‪,‬‬
‫ו‪ BD -‬הוא קוטר במעגל האחר ) ראה ציור (‪.‬‬
‫הוכח כי המר ובע ‪ ACBD‬הוא מקבילית ‪.‬‬
‫‪B‬‬
‫‪90‬‬
‫‪C‬‬
‫‪. 11‬‬
‫‪ AD‬הוא מיתר במעגל החיצוני‬
‫‪O‬‬
‫ו‪ BC -‬הוא מיתר במעגל הפנימי ‪.‬‬
‫הוכח ‪. AB  CD :‬‬
‫‪. 12‬‬
‫‪D‬‬
‫‪C‬‬
‫‪B‬‬
‫‪ AB‬ו‪ DC -‬הם מיתרים במעגל החיצוני ‪,‬‬
‫‪ EF‬ו‪ GH -‬הם מיתרים במעגל הפנימי ‪.‬‬
‫‪C‬‬
‫‪O‬‬
‫‪G‬‬
‫‪H‬‬
‫נתון ‪ . EF  GH :‬הוכח ‪. AB  CD :‬‬
‫‪. 13‬‬
‫‪A‬‬
‫‪E‬‬
‫‪F‬‬
‫‪B‬‬
‫‪A‬‬
‫‪D‬‬
‫‪B‬‬
‫‪ AB‬הוא מיתר במעגל הגדול החותך את המעגל‬
‫‪O‬‬
‫הקטן ו‪ CD -‬הוא מיתר במעגל הגדול שאינו‬
‫ח ותך את המעגל הקטן ) ראה ציור (‪.‬‬
‫הוכח ‪. AB  CD :‬‬
‫‪. 14‬‬
‫‪A‬‬
‫‪D‬‬
‫בציור מתוארים שני מעגלים הנחתכים‬
‫‪C‬‬
‫‪E‬‬
‫בנקודות ‪ A‬ו‪ . B -‬הנקודות ‪ C‬ו‪ D -‬נמצאות‬
‫‪A‬‬
‫על המעגל השמאלי ‪ E ,‬היא נקודה‬
‫על המעגל הימני ‪ – C ,‬מרכז המעגל הימני ‪.‬‬
‫‪C‬‬
‫א ‪ .‬הוכח ‪. ADB  2  AEB :‬‬
‫‪D‬‬
‫ב ‪ .‬הוכח ‪ :‬אם ‪ , AEB  45‬אז ‪ AB‬הוא קוטר‬
‫‪B‬‬
‫במעגל השמאלי ‪.‬‬
‫‪. 15‬‬
‫נתונים מעגלים שמרכזיהם בנקודות ‪ F‬ו‪. E -‬‬
‫‪D‬‬
‫המעגלים נחתכים בנקודות ‪ B‬ו‪. C -‬‬
‫הנקודה ‪ A‬נמצאת על המעגל ‪ F‬ו הנקודה ‪D‬‬
‫נמצאת על המעגל ‪ AB . E‬חותך את מעגל ‪E‬‬
‫בנקודה ‪ . G‬נתון ‪. A  48 :‬‬
‫א ‪ .‬חשב את הזווית ‪. BDC‬‬
‫ב ‪ .‬הוכח ‪. AG  CG :‬‬
‫א ‪. 84 .‬‬
‫‪C‬‬
‫‪E‬‬
‫‪F‬‬
‫‪A‬‬
‫‪91‬‬
‫‪B‬‬
‫‪. 16‬‬
‫בציור מתוארים שני מעגלים הנחתכים‬
‫‪B‬‬
‫בנקודות ‪ B‬ו‪. C -‬‬
‫המרובע ‪ ABCD‬חסום במע גל השמאלי ‪.‬‬
‫‪A‬‬
‫‪E‬‬
‫הנקודות ‪ E‬ו‪ F -‬נמצאות על המשכי‬
‫הקטעים ‪ AB‬ו‪ DC -‬כך שהמרובע ‪BEFC‬‬
‫חסום במעגל הימני ‪ .‬הוכח ‪. AD  EF :‬‬
‫‪. 17‬‬
‫‪D‬‬
‫‪C‬‬
‫‪F‬‬
‫‪B‬‬
‫‪A‬‬
‫המרובע ‪ ABGD‬הוא מקבילית ‪.‬‬
‫הוכח ‪ :‬המרובע ‪CEGF‬‬
‫בר חסימה במעגל ‪.‬‬
‫‪. 18‬‬
‫‪E‬‬
‫‪G‬‬
‫‪C‬‬
‫‪F‬‬
‫‪D‬‬
‫‪ AB‬ו‪ AC -‬הם מיתרים במעגל שמרכזו ‪. O‬‬
‫‪C‬‬
‫המשכי הרדיוסים ‪ BO‬ו‪ CO -‬חותכים‬
‫‪B‬‬
‫את המיתרים ‪ AC‬ו‪ AB -‬בנקודות ‪ D‬ו‪. E -‬‬
‫‪O‬‬
‫נתון ‪. BAC  60 :‬‬
‫‪E‬‬
‫‪D‬‬
‫א ‪ .‬הוכח ‪ :‬המרובע ‪ ADOE‬הוא בר‪ -‬חסימה במעגל ‪.‬‬
‫ב ‪ .‬הוכח ‪. OAE  ODE :‬‬
‫‪. 19‬‬
‫‪A‬‬
‫הקדקודים ‪ B‬ו‪ C -‬של מקבילית ‪ABCD‬‬
‫נמצאים על מ עגל ‪.‬‬
‫‪A‬‬
‫‪B‬‬
‫‪E‬‬
‫א ‪ .‬הוכח ‪ :‬המרובע ‪AEFD‬‬
‫‪F‬‬
‫‪. 20‬‬
‫ב ‪ .‬הוכח ‪. AED  AFD :‬‬
‫‪C‬‬
‫המשולש ‪ ABC‬חסום במעגל כך ש‪BC -‬‬
‫הוא קוטר במעגל ‪ .‬המיתר ‪DE‬‬
‫חותך את הצלע ‪ AC‬בנקודה ‪G‬‬
‫ואת הקוטר ‪ BC‬בנקודה ‪. F‬‬
‫נתון כי המרובע ‪ ABFG‬ניתן‬
‫לחסימה במעגל ‪ .‬הוכח ‪. DF  EF :‬‬
‫‪C‬‬
‫‪92‬‬
‫‪D‬‬
‫‪D‬‬
‫‪A‬‬
‫‪G‬‬
‫‪F‬‬
‫‪E‬‬
‫‪B‬‬
‫‪. 21‬‬
‫בציורים שלפניך מתוארים שני‬
‫‪A‬‬
‫‪F‬‬
‫מעגלים )‪ M‬ו‪ (N -‬בעלי רדיוסים‬
‫שווים ‪ .‬הוכח ‪ :‬אם ‪, A  D‬‬
‫‪E‬‬
‫אז ‪. BC  EF‬‬
‫‪B‬‬
‫‪C‬‬
‫‪D‬‬
‫‪. 22‬‬
‫‪A‬‬
‫‪F‬‬
‫בציורים שלפניך מתוארים שני‬
‫מעגלים )‪ M‬ו‪ (N -‬בעלי רדיוסים‬
‫שווים ‪ .‬הוכח ‪ :‬אם ‪, BC  EF‬‬
‫‪E‬‬
‫‪B‬‬
‫אז ‪. A  D‬‬
‫‪C‬‬
‫‪D‬‬
‫‪. 23‬‬
‫בציורים מתוארים שני מעגלים שווים‬
‫הנחתכים בנקודות ‪ A‬ו‪. B -‬‬
‫‪D‬‬
‫‪A‬‬
‫המשכי המי תרים ‪ CA‬ו‪ CB -‬של המעגל‬
‫השמאלי חותכים את המעגל הימני בנקודות‬
‫‪C‬‬
‫‪ D‬ו‪ E -‬בהתאמה ‪.‬‬
‫א ‪ .‬הוכח ‪. BC  BD :‬‬
‫‪E‬‬
‫ב ‪ .‬הוכח ‪. AC  AE :‬‬
‫‪. 24‬‬
‫‪B‬‬
‫בציור מתוארים שני מעגלים ‪ .‬מנקודה ‪A‬‬
‫‪D‬‬
‫יוצאים שני משיקים למעגלים ‪.‬‬
‫‪B‬‬
‫‪ D , C , B‬ו‪ E -‬הן נקודות השקה ‪.‬‬
‫‪A‬‬
‫א ‪ .‬הוכח ‪. BD  CE :‬‬
‫ב ‪ .‬הוכח ‪. BC  DE :‬‬
‫‪C‬‬
‫‪E‬‬
‫‪. 25‬‬
‫בציור מתוארים שני מעגלים שמרכזיהם‬
‫בנקודות ‪ F‬ו‪ . G -‬מנקודה ‪ A‬יוצאים‬
‫‪D‬‬
‫‪B‬‬
‫שני משיקים למעגלים ‪.‬‬
‫‪ D , C , B‬ו‪ E -‬הן נקודות השקה ‪.‬‬
‫רדיוסו של מעגל ‪ F‬הוא ‪ 4‬ס " מ‬
‫‪G‬‬
‫ורדיוסו של מעגל ‪ G‬הוא ‪ 7‬ס " מ ‪.‬‬
‫נתון ‪. BAC  60 :‬‬
‫‪93‬‬
‫‪F‬‬
‫‪C‬‬
‫‪E‬‬
‫מהו אורך קטע המרכזים ‪? FG‬‬
‫‪A‬‬
‫‪. 26‬‬
‫‪ 6‬ס"מ‪.‬‬
‫בציור מתוארים שני מעגלים ‪.‬‬
‫‪D‬‬
‫‪ DC‬משיק למעגל הימני בנקודה ‪D‬‬
‫ולמעגל הש מאלי בנקודה ‪. C‬‬
‫‪ BE‬משיק למעגל הימני בנקודה ‪E‬‬
‫ולמעגל השמאלי בנקודה ‪. B‬‬
‫הוכח ‪. BE  CD , BC  DE :‬‬
‫‪. 27‬‬
‫‪C‬‬
‫‪E‬‬
‫המעגלים ‪ M‬ו‪ N -‬הם בעלי אותו רדיוס ‪.‬‬
‫הקטע ‪ AB‬משיק למעגל ‪ M‬בנקודה ‪A‬‬
‫ולמעגל ‪ N‬בנקודה ‪. B‬‬
‫א ‪ .‬הוכח ‪. AN  BM :‬‬
‫ב ‪ E .‬היא אמצע הקטע ‪. AN‬‬
‫הוכח ‪. AE  BE :‬‬
‫‪A‬‬
‫‪N‬‬
‫‪. 28‬‬
‫בשרטוט מתוארים מעגל ‪ O‬ומעגל ‪. M‬‬
‫‪ BP‬משיק למעגל ‪ AP , O‬משיק למעגל ‪M‬‬
‫ו‪ PQ -‬הוא מיתר משותף לשני המעגלים ‪.‬‬
‫הוכח ‪. AQP  PQB :‬‬
‫‪. 29‬‬
‫בשרטוט מתוארים מעגל ‪ O‬ומעגל ‪. M‬‬
‫‪ BD‬משיק למעגל ‪ M‬בנקודה ‪B‬‬
‫ו‪ AC -‬משיק למעגל ‪ O‬בנקודה ‪. A‬‬
‫הוכח ‪. AD  BC :‬‬
‫‪M‬‬
‫‪C‬‬
‫‪B‬‬
‫‪B‬‬
‫‪. 30‬‬
‫‪B‬‬
‫‪Q‬‬
‫‪A‬‬
‫‪M‬‬
‫‪O‬‬
‫‪P‬‬
‫‪A‬‬
‫‪C‬‬
‫‪M‬‬
‫‪O‬‬
‫‪B‬‬
‫‪D‬‬
‫‪B‬‬
‫‪ AB‬ו‪ DC -‬הם מיתרים במעגל‬
‫‪E‬‬
‫הגדול המשיקים למעגל הקטן‬
‫‪A‬‬
‫‪O‬‬
‫בנקודות ‪ E‬ו‪ F -‬בהתאמה ‪.‬‬
‫א ‪ .‬הוכח ‪. AE  BE :‬‬
‫‪D‬‬
‫ב ‪ .‬הוכח ‪. AB  DC :‬‬
‫‪94‬‬
‫‪F‬‬
‫‪C‬‬
‫‪. 31‬‬
‫נתונים שני מעגלים הנחתכים בנקודות ‪ A‬ו‪. B -‬‬
‫המשיק למעגל השמאלי בנקודה ‪ A‬חותך את‬
‫‪A‬‬
‫‪D‬‬
‫המעגל השמאלי בנקודה ‪. C‬‬
‫‪ D‬נקודה על המעגל הימני כך ש‪. AB  DC -‬‬
‫הוכח ‪ BD :‬משיק למעגל השמאלי בנקודה ‪. B‬‬
‫‪. 32‬‬
‫‪C‬‬
‫‪B‬‬
‫שני מעגלים לא שווים חותכים את זה בנקודות ‪ A‬ו‪. B -‬‬
‫המשיק לאחד המעגלים בנקודה ‪A‬‬
‫חותך את המעגל האחר בנקודה ‪. C‬‬
‫המשיק למעגל האחר בנקודה ‪A‬‬
‫‪E‬‬
‫‪C‬‬
‫‪G‬‬
‫‪B‬‬
‫חותך את המעגל האחר בנקודה ‪. D‬‬
‫‪A‬‬
‫א ‪ .‬הוכח ‪. ABC  ABD :‬‬
‫‪D‬‬
‫ב ‪ .‬ישר העובר דרך הנקודה ‪ A‬חותך את אחד‬
‫המעגלים בנקודה ‪ F‬ואת המעגל האחר – בנקודה ‪. E‬‬
‫‪F‬‬
‫הישרים ‪ EC‬ו‪ FD -‬נפגשים בנקודה ‪. G‬‬
‫הוכח ‪ :‬המשולש ‪ EFG‬הוא שווה‪ -‬שוקיים ‪.‬‬
‫‪. 33‬‬
‫על הרדיוס ‪ OB‬של רבע מעגל ‪AOB‬‬
‫בנו מעגל ‪ D‬שקוטרו הוא הקטע ‪. OB‬‬
‫א ‪ .‬הוכח ‪ AO :‬משיק למעגל ‪. D‬‬
‫ב ‪ AB .‬חותך את המעגל ‪ D‬בנקודה ‪. E‬‬
‫הוכח ‪. AE  BE :‬‬
‫‪. 34‬‬
‫בציור שלפניך הנקודה ‪ M‬היא מרכז‬
‫‪A‬‬
‫‪E‬‬
‫‪B‬‬
‫‪O‬‬
‫‪D‬‬
‫‪A‬‬
‫המעגל החוסם את המשולש ‪ADE‬‬
‫והנקודה ‪ N‬היא מרכז המעגל‬
‫הוכח ‪. DM  BN :‬‬
‫‪M‬‬
‫‪E‬‬
‫‪D‬‬
‫‪N‬‬
‫‪C‬‬
‫‪. 35‬‬
‫‪B‬‬
‫בציור מתוארים שני מעגלים המשיקים‬
‫זה לזה מבחוץ בנקודה ‪ – D . B‬מרכז‬
‫המעגל השמאלי ‪ – E ,‬מרכז המעגל‬
‫הימני ‪ .‬נתון ‪ 6 :‬ס " מ ‪ 8 , AB ‬ס " מ ‪. BC ‬‬
‫חשב את אורך קטע המרכזים )‪. (DE‬‬
‫‪95‬‬
‫‪C‬‬
‫‪E‬‬
‫‪B‬‬
‫‪D‬‬
‫‪A‬‬
‫‪. 36‬‬
‫‪ 7‬ס"מ‪.‬‬
‫שני מעגלים משיקים זה לזה מבפנים ‪ .‬קוט ר המעגל הגדול הוא ‪ 12‬ס " מ‬
‫ואורך קטע המרכזים הוא ‪ 4‬ס " מ ‪ .‬מהו אורך רדיוס המעגל הקטן ?‬
‫‪. 37‬‬
‫‪ 2‬ס"מ‪.‬‬
‫נתונים שני מעגלים שרדיוסיהם ‪ R1‬ו‪ . (R1  R 2 ) R 2 -‬כאשר המעגלים‬
‫משיקים זה לזה מבפנים ‪ ,‬אורך קטע המרכזים הוא ‪ 7‬ס " מ ‪ ,‬וכאשר‬
‫המעגלים משיקים זה לזה מבחוץ ‪ ,‬אורך קטע המרכזים הוא ‪ 15‬ס " מ ‪.‬‬
‫מצא את ‪ R1‬ו‪. R 2 -‬‬
‫‪. 38‬‬
‫‪ 11‬ס " מ ‪ 4 , R1 ‬ס " מ ‪. R 2 ‬‬
‫המעגלים ‪ M‬ו‪ N -‬המתוארים בציור משיק ים‬
‫‪A‬‬
‫זה לזה בנקודה ‪ . C‬המשיק המשותף‬
‫לשני המעגלים ‪ ,‬העובר דרך נקודה ‪, D‬‬
‫נוגע במעגל ‪ N‬בנקודה ‪B‬‬
‫ובמעגל ‪ M‬בנקודה ‪. A‬‬
‫א ‪ .‬הוכח ‪. ACB  90 :‬‬
‫ב ‪ .‬הוכח ‪. DBC  DCA :‬‬
‫‪D‬‬
‫‪B‬‬
‫‪C‬‬
‫‪N‬‬
‫‪M‬‬
‫‪D‬‬
‫‪. 39‬‬
‫שני מעגלים משיקים זה לזה בנקודה ‪. A‬‬
‫‪E‬‬
‫‪ AB‬ו‪ AC -‬הם מיתרים במעגל הקטן ‪.‬‬
‫‪B‬‬
‫‪ AD‬ו‪ AE -‬הם מיתרים במעגל הגדול ‪.‬‬
‫‪C‬‬
‫הוכח ‪. BC  DE :‬‬
‫‪A‬‬
‫‪. 40‬‬
‫שני מעגלים משיקים מבפנים בנקודה ‪. A‬‬
‫‪A‬‬
‫‪ BC‬הוא מיתר במעגל הגדול המשיק‬
‫למעגל הקטן בנקודה ‪. D‬‬
‫‪F‬‬
‫המיתרים ‪ AB‬ו‪ AC -‬חותכים את המעגל‬
‫הקטן בנקודות ‪ E‬ו‪ F -‬בהתאמה ‪.‬‬
‫א ‪ .‬הוכח ‪. ADF  ABC :‬‬
‫ב ‪ .‬הוכח ‪. EAF  BDE  CDF :‬‬
‫‪96‬‬
‫‪C‬‬
‫‪E‬‬
‫‪D‬‬
‫‪B‬‬
‫‪. 41‬‬
‫‪D‬‬
‫זה לזה מבפנים בנקודה ‪. A‬‬
‫‪B‬‬
‫‪ – C‬מרכז המעגל הגדול ‪.‬‬
‫‪E‬‬
‫‪ AC‬הוא קוטר ב מעגל ה קטן ‪.‬‬
‫‪A‬‬
‫‪C‬‬
‫א ‪ .‬הוכח ‪. BC  DE :‬‬
‫ב ‪ .‬הוכח ‪. AB  BD :‬‬
‫‪. 42‬‬
‫‪A‬‬
‫‪B‬‬
‫זה לזה מבחוץ בנקודה ‪. E‬‬
‫‪ A‬ו‪ D -‬הן נקודות על המעגל השמאלי ‪.‬‬
‫‪E‬‬
‫המשכי הקטעים ‪ AE‬ו‪ DE -‬חותכי ם‬
‫את המעגל הימני בנקודות ‪ C‬ו‪. B -‬‬
‫‪D‬‬
‫א ‪ .‬הוכח ‪. AD  BC :‬‬
‫‪C‬‬
‫ב ‪ .‬הוכח ‪ :‬המשיק למעגל הימני בנקודה ‪B‬‬
‫מקביל למשיק למעגל השמאלי בנקודה ‪. D‬‬
‫‪. 43‬‬
‫המעגלים ‪ M‬ו‪ N -‬הם בעלי אותו‬
‫רדיוס ‪ .‬המעגלים משיקים זה לזה‬
‫בנקודה ‪. A‬‬
‫‪B‬‬
‫‪N‬‬
‫‪A‬‬
‫‪M‬‬
‫‪C‬‬
‫‪. 44‬‬
‫הוכח את המשפט ‪ :‬קטע המרכזים של שני מעגלים נחתכים חוצה‬
‫את המיתר המשותף ומאונך לו ‪.‬‬
‫‪. 45‬‬
‫הוכח את המשפט ‪ :‬נקודות ההשקה של שני מעגלים המשיקים‬
‫מבחוץ נמצאת על קטע המרכזים ‪.‬‬
‫‪. 46‬‬
‫הוכח את המשפט ‪ :‬נקודת ההשקה של שני מעגלים המשיקים‬
‫מב פ נים נמצאת על המשכ ו של קטע המרכזים ‪.‬‬
‫‪97‬‬

מעגל החוסם משולש

Transcription

Similar documents

) ` ח כיתה – למדא / " בריבוע עשר "(

דוגמא למבחן - אוניברסיטת תל אביב

בעיות בהנדסת המישור - מתמטיקה-המדריך המלא לפתרון תרגילים

` כיתה ח – דימיון משולשים

ג רמה רגילה טור ג

חוברת מתכונות שאלון ה.pdf 164.5 Kb

טריגונומטריה 3.

Aleph – Ohel, Bet ze Bait - בַּיִת זֶה ` ב, אֹהֶ ל `א

תיקונים לספר כיתה י

46 . -M . האלכסונים נפגשים ב במלבן . - העלו אנך ל מנקודה .( ראה ציור ) בנקודה

מבוא הספר - פירוש אליהו