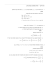נוסחאות הדרושות לפרק זה:

‫מתמטיקה בהישג יד ‪3 -‬‬
‫חשבון‬
‫דפרנציאלי‬
‫דודו גולדשטיין‬
‫מתמטיקה בהישג יד ‪803 -‬‬
‫דודו גולדשטיין‬
‫חשבון דפרנציאלי‬
‫נגזרות של פולינום‪:‬‬
‫הביטוי‬
‫‪x3 + 2x2 + 5x‬‬
‫פעולת הנגזרת ‪-‬‬
‫‪x3 , 2x2 , 5x‬‬
‫הוא פולינום המורכב משלושה מונומים‪:‬‬
‫כשגוזרים מונום המעלה שלו יורדת ב‪ 1 -‬באופן הבא‪:‬‬
‫‪→ y' = 2•4x1 = 8x‬‬
‫‪y = 4x2‬‬
‫‪y' = 3x2‬‬
‫‪,‬‬
‫→‬
‫‪y = x3‬‬
‫גזרו את הפונקציות‪:‬‬
‫= )‪f '(x‬‬
‫‪f(x) = 2x5‬‬
‫)‪(5‬‬
‫= '‪y‬‬
‫‪y = x4‬‬
‫)‪(1‬‬
‫= )‪g '(x‬‬
‫‪g(x) = 6x3‬‬
‫)‪(6‬‬
‫= '‪y‬‬
‫‪y = x6‬‬
‫)‪(2‬‬
‫= )‪f '(x‬‬
‫‪f(x) = -3x2‬‬
‫)‪(7‬‬
‫= '‪y‬‬
‫‪y = x3‬‬
‫)‪(3‬‬
‫= '‪y‬‬
‫‪y = -x8‬‬
‫)‪(8‬‬
‫= '‪y‬‬
‫‪y = 4x3‬‬
‫)‪(4‬‬
‫בגזירה של פולינום יש לגזור איבר איבר‪ .‬לדוגמה‪:‬‬
‫‪y' = 12x2 – 2x‬‬
‫>– ‪y = 4x3 – x2‬‬
‫גזרו את הפונקציות‪:‬‬
‫‪1‬‬
‫= )‪f '(x‬‬
‫‪f(x) = 2x5 + 9x2‬‬
‫)‪(1‬‬
‫= )‪f '(x‬‬
‫‪f(x) = -x3 – 5x4‬‬
‫)‪(2‬‬
‫= '‪y‬‬
‫‪y = 2x4 – 3x2 – 5x6‬‬
‫)‪(3‬‬
‫= '‪y‬‬
‫‪y = 4x6 + 2x3 – 2x2‬‬
‫)‪(4‬‬
‫© כל הזכויות שמורות‪ .‬אין לצלם או להעתיק חוברת זו ללא אישור מהמחבר‪.‬‬
‫‪lomdimbareshet.net‬‬
‫מתמטיקה בהישג יד ‪803 -‬‬
‫דודו גולדשטיין‬
‫חשבון דפרנציאלי‬
‫בנגזרת של איבר ממעלה ראשונה ‪ -‬המשתנה "יורד”‪ .‬דוגמאות‪:‬‬
‫‪y = x → y' = 1‬‬
‫‪,‬‬
‫‪,‬‬
‫‪y = -2x → y' = -2‬‬
‫‪y = 5x → y' = 5‬‬
‫הנגזרת של מספר מוגדרת כ‪ . 0 -‬דוגמאות‪:‬‬
‫‪y = 5 –> y' = 0‬‬
‫‪,‬‬
‫‪y' = 0‬‬
‫‪,‬‬
‫>– ‪y = -4.23‬‬
‫‪y = 6 → y' = 0‬‬
‫גזרו את הפונקציות‪:‬‬
‫= )‪f '(x‬‬
‫‪f(x) = 5x‬‬
‫)‪(1‬‬
‫= )‪f '(x‬‬
‫‪f(x) = 7‬‬
‫)‪(2‬‬
‫= '‪y‬‬
‫‪y = -2‬‬
‫)‪(3‬‬
‫= )‪g '(x‬‬
‫‪g(x) = -6x‬‬
‫)‪(4‬‬
‫= '‪y‬‬
‫‪y = 4.5x – 3‬‬
‫)‪(5‬‬
‫= )‪f '(x‬‬
‫‪f(x) = 3x2 – 4x – 3‬‬
‫)‪(6‬‬
‫= )‪f '(x‬‬
‫‪f(x) = -4x3 – 2x + 1‬‬
‫)‪(7‬‬
‫= '‪y‬‬
‫‪y = 3x4 + x – 2‬‬
‫)‪(8‬‬
‫= )‪g '(x‬‬
‫‪g(x) = 6x + 7.6‬‬
‫)‪(9‬‬
‫= '‪y‬‬
‫‪y = 5x3 + 4x – 4.5‬‬
‫)‪(10‬‬
‫כל הנגזרות שביצענו עד כה ‪ ,‬נעשו בהתאם לנוסחה לגזירת מונום‪:‬‬
‫‪2‬‬
‫© כל הזכויות שמורות‪ .‬אין לצלם או להעתיק חוברת זו ללא אישור מהמחבר‪.‬‬
‫‪(Xn)' = n•Xn-1‬‬
‫‪lomdimbareshet.net‬‬
‫מתמטיקה בהישג יד ‪803 -‬‬
‫חשבון דפרנציאלי‬
‫גזירת פונקציות‬
‫עם‬
‫דודו גולדשטיין‬
‫מספר‬
‫במכנה‬
‫בגזירת שבר עם מספר במכנה – גוזרים את המונה בלבד‪:‬‬
‫דוגמאות‪:‬‬
‫‪3‬‬
‫‪2‬‬
‫‪x‬‬
‫‪3x‬‬
‫‪2‬‬
‫= '‪→ y‬‬
‫= ‪y‬‬
‫‪= x‬‬
‫‪3‬‬
‫‪3‬‬
‫‪4‬‬
‫‪3‬‬
‫‪2x − 4x‬‬
‫‪8x − 4‬‬
‫‪3‬‬
‫= '‪→ y‬‬
‫= ‪y‬‬
‫‪= 2x − 1‬‬
‫‪4‬‬
‫‪4‬‬
‫גזרו את הפונקציות‪:‬‬
‫‪4‬‬
‫‪x‬‬
‫‪4‬‬
‫= )‪f '(x‬‬
‫‪3‬‬
‫= )‪f '(x‬‬
‫= )‪f ( x‬‬
‫)‪(1‬‬
‫‪−3x‬‬
‫= )‪f ( x‬‬
‫‪9‬‬
‫)‪(2‬‬
‫‪2x‬‬
‫= ‪y‬‬
‫‪4‬‬
‫)‪(3‬‬
‫‪4‬‬
‫= '‪y‬‬
‫‪3‬‬
‫‪2x − 3x‬‬
‫‪2‬‬
‫‪+ 5x‬‬
‫‪3‬‬
‫= ‪y‬‬
‫)‪(4‬‬
‫‪x − 10x‬‬
‫= ‪y‬‬
‫‪+ 4x + 1‬‬
‫‪5‬‬
‫)‪(5‬‬
‫‪−x − 3x‬‬
‫‪4‬‬
‫= )‪f ( x‬‬
‫‪− 3x + 2x‬‬
‫‪6‬‬
‫)‪(6‬‬
‫‪5‬‬
‫‪2‬‬
‫‪3‬‬
‫© כל הזכויות שמורות‪ .‬אין לצלם או להעתיק חוברת זו ללא אישור מהמחבר‪.‬‬
‫‪6‬‬
‫‪lomdimbareshet.net‬‬
‫מתמטיקה בהישג יד ‪803 -‬‬
‫דודו גולדשטיין‬
‫חשבון דפרנציאלי‬
‫נגזרת שניה‪:‬‬
‫הנגזרת של הנגזרת נקראת נגזרת שנייה‪ .‬דוגמה‪:‬‬
‫‪y' = 3x2 → y'' = 6x‬‬
‫>– ‪y = x3‬‬
‫מצאו את הנגזרת ואת הנגזרת השנייה של הפונקציות הבאות‪:‬‬
‫‪g(x) = 4x – 4.7‬‬
‫)‪(5‬‬
‫= )‪g'(x‬‬
‫= )‪f '(x‬‬
‫= )‪g''(x‬‬
‫= )‪f ''(x‬‬
‫‪y = 2x6 – 6x + 2.2‬‬
‫‪f(x) = -3x2 + 3‬‬
‫)‪(6‬‬
‫= '‪y‬‬
‫= )‪f '(x‬‬
‫= ''‪y‬‬
‫= )‪f ''(x‬‬
‫‪y = x5 – 4x2 + 6.1‬‬
‫‪y = 3x4 + x – 2‬‬
‫)‪(7‬‬
‫= '‪y‬‬
‫= '‪y‬‬
‫= ''‪y‬‬
‫= ''‪y‬‬
‫‪y = 3x3 + 4x2‬‬
‫‪4‬‬
‫‪f(x) = 5x3 – 4x‬‬
‫)‪(8‬‬
‫‪y = 2x5 + 2x + 2‬‬
‫= '‪y‬‬
‫= '‪y‬‬
‫= ''‪y‬‬
‫= ''‪y‬‬
‫© כל הזכויות שמורות‪ .‬אין לצלם או להעתיק חוברת זו ללא אישור מהמחבר‪.‬‬
‫‪lomdimbareshet.net‬‬
‫)‪(1‬‬
‫)‪(2‬‬
‫)‪(3‬‬
‫)‪(4‬‬
‫מתמטיקה בהישג יד ‪803 -‬‬
‫חשבון דפרנציאלי‬
‫מציאת ערך‬
‫דודו גולדשטיין‬
‫הנגזרת‬
‫דוגמה‬
‫נתונה הפונקציה‬
‫‪. y = 2.5x2 – 6x‬‬
‫שלב ‪ : I‬גוזרים את פונקציה‪:‬‬
‫‪y' = 5x – 6‬‬
‫שלב ‪ :II‬לחישוב ערך הנגזרת מציבים בה ערכי ‪ . x‬דוגמאות‪:‬‬
‫‪x = 0‬‬
‫‪x = 2‬‬
‫‪x = 1‬‬
‫‪y' = 5x – 6‬‬
‫‪y' = 5x – 6‬‬
‫‪y' = 5x – 6‬‬
‫‪y' = 5•(0) – 6 = -6‬‬
‫‪y' = 5•(1) – 6 = -1‬‬
‫‪y' = 5•(2) – 6 = 4‬‬
‫ערך הנגזרת הוא ‪-6‬‬
‫ערך הנגזרת הוא ‪4‬‬
‫ערך הנגזרת הוא ‪-1‬‬
‫מצאו את ערך הנגזרות עבור ערכי ה – ‪ x‬הנתונים‪:‬‬
‫‪2‬‬
‫‪f(x) = x – 4x‬‬
‫= )‪f '(x‬‬
‫‪x = 0‬‬
‫)‪(3‬‬
‫‪x = 1‬‬
‫)‪(2‬‬
‫‪x = 5‬‬
‫)‪(6‬‬
‫‪x = -3‬‬
‫)‪(5‬‬
‫‪x = 2‬‬
‫‪1 3‬‬
‫‪x −x‬‬
‫‪3‬‬
‫)‪(1‬‬
‫= ‪y‬‬
‫= '‪y‬‬
‫‪, 0 (1‬‬
‫‪5‬‬
‫‪x = 3‬‬
‫‪24 (6 , 8 (5 , 8 (4 , -4 (3 , -2 (2‬‬
‫© כל הזכויות שמורות‪ .‬אין לצלם או להעתיק חוברת זו ללא אישור מהמחבר‪.‬‬
‫‪lomdimbareshet.net‬‬
‫)‪(4‬‬
‫מתמטיקה בהישג יד ‪803 -‬‬
‫חשבון דפרנציאלי‬
‫הנגזרת כשיפוע‬
‫השיפוע של הפוקציה הקווית‬
‫המשיק‬
‫‪ y = 2x – 4‬הוא‬
‫ונגזרת הפונקציה היא‬
‫דודו גולדשטיין‬
‫לפונקציה‪:‬‬
‫‪.m = 2‬‬
‫_____ = '‪y‬‬
‫ניתן להבחין שהנגזרת של הפונקציה הקווית שווה לשיפוע שלה‪ .‬כלומר‪y' = m = 2 :‬‬
‫הנגזרת מוגדרת כשיפוע המשיק לפונקציה‪.‬‬
‫משיק – ישר הנושק לפונקציה בנקודה‬
‫אחת בסביבת הנקודה ‪.‬‬
‫שיפוע המשיק שווה לערך הנגזרת‬
‫בנקודת ההשקה‬
‫) ‪m  f (x‬‬
‫נתבונן בגרף הפונקציה הריבועית‬
‫‪ f(x) = 4x + x2‬ונסרטט שלושה משיקים בשלוש נקודות‪:‬‬
‫)‪A(-1 , -3) , B(-3 , -3) , C(-2 , -4‬‬
‫באמצעות הנגזרת נמצא את שיפועי המשיקים בכל אחת מהנקודות‪.‬‬
‫‪f '(x) = 4 + 2x‬‬
‫) שימו לב שהגרף עולה(‬
‫‪f '(-1) = 4 + 2•(-1) = 2 → m = 2‬‬
‫‪f '(-2) = 4 + 2•(-2) = 0 → m = 0‬‬
‫) שימו לב שהגרף יורד(‬
‫‪6‬‬
‫‪f '(-3) = 4 + 2•(-3) = -2 → m = -2‬‬
‫© כל הזכויות שמורות‪ .‬אין לצלם או להעתיק חוברת זו ללא אישור מהמחבר‪.‬‬
‫‪lomdimbareshet.net‬‬
‫מתמטיקה בהישג יד ‪803 -‬‬
‫דודו גולדשטיין‬
‫חשבון דפרנציאלי‬
‫פתרו את התרגיל מימין בהתאם לדוגמה הפתורה משמאל‪:‬‬
‫חשבו את שיפוע המשיק לפונקציה‬
‫‪y = -x3‬‬
‫בנקודה )‪C(1 , -1‬‬
‫חשבו את שיפוע המשיק לפונקציה‬
‫‪y = 2x2‬‬
‫בנקודה )‪A(1 , 2‬‬
‫פתרון‪:‬‬
‫ראשית נמצא את נגזרת‬
‫הפונקציה‪:‬‬
‫‪y' = 4x‬‬
‫כדי למצוא את השיפוע‬
‫נציב בנגזרת ‪x = 1‬‬
‫‪y' (1) = 4•(1) = 4‬‬
‫תשובה‪:‬‬
‫שיפוע המשיק בנקודה ‪ A‬הוא ‪m = 4‬‬
‫חשבו את שיפוע משיקי הפונקציות בנקודות הנתונות‪:‬‬
‫שיפוע המשיק‬
‫‪M = 3•(2)2 = 12‬‬
‫‪7‬‬
‫נגזרת‬
‫נקודת השקה‬
‫פונקציה‬
‫‪Y' = 3x2‬‬
‫)‪(2 , 8‬‬
‫‪y = x3‬‬
‫)‪(1‬‬
‫= )‪f '(x‬‬
‫)‪(2 , 0‬‬
‫‪f(x) = 2x – x2‬‬
‫)‪(2‬‬
‫)‪(1 , -1‬‬
‫‪y = x3 – 2x‬‬
‫)‪(3‬‬
‫)‪(2 , 12‬‬
‫‪y = 2x3 – x2‬‬
‫)‪(4‬‬
‫)‪(0 , -3‬‬
‫‪y = 3x2 – 3‬‬
‫)‪(5‬‬
‫)‪(-1 , -1‬‬
‫‪y = x4 – 2x2‬‬
‫)‪(6‬‬
‫)‪(0 , 0‬‬
‫‪y = 4x2 – 3x‬‬
‫)‪(7‬‬
‫© כל הזכויות שמורות‪ .‬אין לצלם או להעתיק חוברת זו ללא אישור מהמחבר‪.‬‬
‫‪lomdimbareshet.net‬‬
‫מתמטיקה בהישג יד ‪803 -‬‬
‫חשבון דפרנציאלי‬
‫משוואת‬
‫דודו גולדשטיין‬
‫המשיק לפונקציה‪:‬‬
‫משיק הוא ישר ולכן נחזור להשתמש במשוואת הישר‪:‬‬
‫‪y = mx + b‬‬
‫כפי שלמדתם ביחידת הלימוד "גאומטריה אנליטית ‪ , ”801‬כדי למצוא משוואת ישר‬
‫עלינו לגלות את השיפוע ואת החיתוך עם ציר ‪ . y‬כלומר‪ ,‬עלינו לחשב את ‪ m‬ואת ‪. b‬‬
‫פתרו את התרגיל מימין בהתאם לדוגמה הפתורה משמאל‪:‬‬
‫מצאו את משוואת המשיק לפונקציה‬
‫מצאו את משוואת המשיק לפונקציה‬
‫‪y = -x3 + 1‬‬
‫בנקודה שבה ‪x = 1‬‬
‫‪y = 2x2 – 12‬‬
‫בנקודה שבה ‪x = 2‬‬
‫פתרון‪:‬‬
‫שלב ‪ – I‬מציאת שיפוע המשיק‪:‬‬
‫את שיפוע המשיק מוצאים באמצעות הנגזרת‪:‬‬
‫‪y' = 4x‬‬
‫נציב בנגזרת ‪: x = 2‬‬
‫‪y' (2) = 4•(2) = 8‬‬
‫שיפוע המשיק בנקודה הוא ‪m = 8‬‬
‫שלב ‪ – II‬מציאת ‪ Y‬של נקודת ההשקה ‪:‬‬
‫כדי למצוא את ‪ y‬מציבים את ‪ x‬בפונקציה‪:‬‬
‫‪y = 2x2 – 12‬‬
‫‪y = 2•(2)2 – 12 = -4‬‬
‫שלב ‪ – III‬הצבה במשוואת הישר‪:‬‬
‫נציב את כל הנתונים במשוואת הישר‪:‬‬
‫‪y = mx + b‬‬
‫‪-4 = 8•(2) + b‬‬
‫‪==> -20 = b‬‬
‫תשובה‪:‬‬
‫‪8‬‬
‫‪-4 = 16 + b‬‬
‫‪y = 8x – 20‬‬
‫© כל הזכויות שמורות‪ .‬אין לצלם או להעתיק חוברת זו ללא אישור מהמחבר‪.‬‬
‫‪lomdimbareshet.net‬‬
‫מתמטיקה בהישג יד ‪803 -‬‬
‫דודו גולדשטיין‬
‫חשבון דפרנציאלי‬
‫תרגול‪:‬‬
‫)‪ (1‬מצאו את שיפוע המשיק לפונקציה ‪y = 2x3 – 2x‬‬
‫בנקודה שבה ‪. x = 1‬‬
‫)‪ (2‬העבירו משיק לפונקציה‬
‫‪y = x3 – 6x‬‬
‫בנקודה שבה ‪. x = 2‬‬
‫א‪ .‬מצאו את שיפוע המשיק‪.‬‬
‫ב‪ .‬מצאו את משוואת המשיק‪.‬‬
‫)‪(3‬‬
‫א‪ .‬מצאו את משוואת המשיק של הפרבולה‪ y = 8x2 – 5 :‬בנקודה‬
‫‪1‬‬
‫)‪, −3‬‬
‫‪2‬‬
‫(‪A‬‬
‫ב‪ .‬מצאו את נקדת החיתוך של המשיק עם הצירים‪.‬‬
‫)‪ (4‬נתונה הפונקציה‪:‬‬
‫‪1 3‬‬
‫‪x − 4x‬‬
‫‪3‬‬
‫= ‪ . y‬מעבירים משיק לגרף הפונקציה‬
‫בנקודה שבה ‪. x = 3‬‬
‫א‪ .‬חשבו את שיפוע המשיק‪.‬‬
‫ב‪ .‬מצאו את משוואת המשיק‪.‬‬
‫‪1) m = 4 , 2) y = 6x – 16 , 3) y = 8x – 7 , (0, -7) (0.875, 0) , 4) y = 5x - 18‬‬
‫‪9‬‬
‫© כל הזכויות שמורות‪ .‬אין לצלם או להעתיק חוברת זו ללא אישור מהמחבר‪.‬‬
‫‪lomdimbareshet.net‬‬
‫מתמטיקה בהישג יד ‪803 -‬‬
‫דודו גולדשטיין‬
‫חשבון דפרנציאלי‬
‫פתרו את התרגיל מימין בהתאם לדוגמה הפתורה משמאל‪:‬‬
‫נתונה הפונקציה‬
‫‪f(x) = -x2 + 5x‬‬
‫מצאו את ‪ x‬עבורו שיפוע המשיק הוא ‪1‬‬
‫‪1 3‬‬
‫‪x − 4x 2 + 10x‬‬
‫‪3‬‬
‫נתונה הפונקציה‬
‫=‪y‬‬
‫מצאו את ‪ x‬עבורו שיפוע המשיק הוא ‪-6‬‬
‫פתרון‪:‬‬
‫שיפוע המשיק בנקודה שווה לערך הנגזרת‪.‬‬
‫לכן ניתן לרשום את הנתון כך‪:‬‬
‫‪y' = -6‬‬
‫נגזור את הפונקציה ונשווה ל‪-6 -‬‬
‫‪y' = x2 – 8x + 10‬‬
‫‪x2 – 8x + 10 = -6‬‬
‫נפתור את המשוואה הריבועית שהתקבלה‬
‫‪x2 – 8x + 16 = 0‬‬
‫‪a = 1 , b = -8 , c = 16‬‬
‫‪−(−8) ± √ (−8)2−4 •1 • 16 8 ± 0‬‬
‫=‬
‫‪2• 1‬‬
‫‪2‬‬
‫=‪X 1, 2‬‬
‫‪X = 4‬‬
‫תשובה‪:‬‬
‫בנקודה שבה ‪ x = 4‬שיפוע המשיק הוא ‪-6‬‬
‫תרגול‪:‬‬
‫)‪ (1‬נתונה הפונקציה‪. y = 2x2 + 4x :‬‬
‫מצאו את הערך של ‪ x‬שבו שיפוע המשיק הוא ‪. 0‬‬
‫)‪(2‬‬
‫נתונה הפונקציה‪. y = -3x2 – 6x :‬‬
‫שיפוע המשיק בנקודה ‪ A‬הוא ‪.12‬‬
‫מצאו את שיעורי הנקודה ‪.A‬‬
‫‪10‬‬
‫© כל הזכויות שמורות‪ .‬אין לצלם או להעתיק חוברת זו ללא אישור מהמחבר‪.‬‬
‫‪lomdimbareshet.net‬‬
‫מתמטיקה בהישג יד ‪803 -‬‬
‫חשבון דפרנציאלי‬
‫דודו גולדשטיין‬
‫)‪ (3‬נתונה הפונקציה‪. y = 4x2 – x :‬‬
‫שיפוע המשיק בנקודה ‪ A‬הוא ‪.7‬‬
‫מצאו את שיעורי הנקודה ‪.A‬‬
‫`‬
‫)‪ (4‬נתונה הפונקציה‪. y = x3 + 3x2 + 2x :‬‬
‫שיפוע המשיק בנקודה ‪ B‬הוא ‪-1‬‬
‫מצאו את שיעורי הנקודה ‪.B‬‬
‫)‪ (5‬נתונה הפונקציה ‪ . f(x) = x3 – 6x + 2‬לגרף הפונקציה מעבירים שני משיקים‬
‫ששיפוע כל אחד מהם הוא ‪.21‬‬
‫מצאו את שיעורי נקודות ההשקה של שני המשיקים‪.‬‬
‫)‪1) x = -3 , 2) A(-3 , -9) , 3) A(1, 3) , 4) B(-1 , 0) , 5) (3 , 11) (-3 , -7‬‬
‫‪11‬‬
‫© כל הזכויות שמורות‪ .‬אין לצלם או להעתיק חוברת זו ללא אישור מהמחבר‪.‬‬
‫‪lomdimbareshet.net‬‬