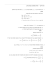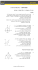מציאת משיק ונורמל

‫מציאת משיק ונורמל‬
‫הסבר והקדמה‬
‫אם לפונקציה )‪ f (x‬יש נגזרת בנקודה ) ‪ P( x0 ; y 0‬אזי לעקום יש משיק בנקודה‬
‫זו ‪.‬המשיק הוא קו ישר אשר ניתן לתיאור באמצעות‬
‫או‬
‫) ‪y  y 0  m( x  x0‬‬
‫כאשר‬
‫‪y  mx  k‬‬
‫‪ m‬זו הנגזרת בנקודה ההשקה‪.‬‬
‫‪y‬‬
‫המשיק בנקודה הוא הקו המרוסק‪.‬‬
‫ויוצר זוית ‪ ‬עם ציר ה ‪x‬‬
‫)‪P(x0;y0‬‬
‫‪y0‬‬
‫‪‬‬
‫‪x‬‬
‫‪x0‬‬
‫אם נגזור את‬
‫‪ f ( x)  y‬נקבל את '‪ f ' ( x)  y‬ובנקודת ההשקה שיפוע‬
‫‪ f ' ( x0 )  m‬אם נציב זאת‬
‫המשיק זהה בדיוק לשיפוע הפונקציה ולכן‬
‫) ‪. y  y0  f ' ( x0 )( x  x0‬‬
‫בישר המשיק נקבל את משוואת הישר‬
‫את ערכי הנקודה יש לנו וכן את הנגזרת בנקודה ומהן נקבל את הישר‪.‬‬
‫) ‪y  y 0  m( x  x0‬‬
‫דוגמא‪:‬‬
‫נתונה הפונקציה‬
‫‪y  x 2  3x  4‬‬
‫מצא את המשיק בנקודות‬
‫)‪P1 (0;4‬‬
‫ו‬
‫)‪. P2 (3;4‬‬
‫פתרון‪:‬‬
‫‪y  x 2  3x  4‬‬
‫‪y'  2 x  3‬‬
‫נחשב את הנגזרת‬
‫נציב את הנקודות בנקודה )‪ P1 (0;4‬נקבל‬
‫‪m1  2 * 0  3  3‬‬
‫ובנקודה )‪ P2 (3;4‬נקבל‬
‫‪m2  2 * 3  3  3‬‬
‫נצייר את הגרף‬
‫‪y‬‬
‫‪y=x2-3x+4‬‬
‫‪6‬‬
‫‪5‬‬
‫‪p2‬‬
‫‪4‬‬
‫‪p1‬‬
‫‪3‬‬
‫‪2‬‬
‫‪1‬‬
‫‪X‬‬
‫‪9‬‬
‫‪8‬‬
‫‪7‬‬
‫‪6‬‬
‫‪5‬‬
‫‪4‬‬
‫‪3‬‬
‫‪1‬‬
‫‪2‬‬
‫‪0‬‬
‫‪-1‬‬
‫‪-1‬‬
‫‪-2‬‬
‫הקוים המרוסקים הם המשיקים בנקודות‬
‫‪-3‬‬
‫‪-4‬‬
‫נכתוב את משוואת המשיק ל‬
‫)‪P1 (0;4‬‬
‫) ‪y  y 0  m( x  x 0‬‬
‫)‪y  4  3( x  0‬‬
‫‪y  3x  4‬‬
‫והמשיק לנקודה‬
‫)‪P2 (3;4‬‬
‫)‪y  4  3( x  3‬‬
‫‪y  3x  5‬‬
‫הנורמל הוא הישר המאונך למשיק בנקודת ההשקה‪.‬‬
‫‪y‬‬
‫המשיק בנקודה הוא הקו המרוסק‪.‬‬
‫ויוצר זוית ‪ ‬עם ציר ה ‪x‬‬
‫‪N‬‬
‫)‪P(x0;y0‬‬
‫‪y0‬‬
‫‪‬‬
‫‪x‬‬
‫‪x0‬‬
‫הנורמל מסומן ב ‪ . N‬אנו יודעים את שיפוע המשיק ‪ m‬ומכאן שיפוע‬
‫‪1‬‬
‫הנורמל יהיה‬
‫‪m‬‬
‫‪ ‬ומשוואת הנורמל העובר בנקודת ההשקה תהיה‬
‫‪1‬‬
‫) ‪( x  x0‬‬
‫‪m‬‬
‫‪y  y0  ‬‬
‫אם נציב בדוגמא שלנו נקבל את משוואת הנורמל‬
‫‪1‬‬
‫‪( x  0) ‬‬
‫‪3‬‬
‫בנקודה )‪p1(0;4‬‬
‫‪y4‬‬
‫‪1‬‬
‫‪y x4‬‬
‫‪3‬‬
‫או‬
‫‪x  3 y  12  0‬‬
‫ובנקודה )‪P2(3;4‬‬
‫‪1‬‬
‫‪( x  3) ‬‬
‫‪3‬‬
‫‪1‬‬
‫‪y  4   x 1‬‬
‫‪3‬‬
‫‪x  3 y  15  0‬‬
‫‪y4‬‬
‫תרגיל‬
‫‪ .1‬נתונה הפונקציה‬
‫בנקודה )‪P(2;4‬‬
‫מצא את המשיק ואת הנורמל‬
‫‪y  x 3  2x 2  4‬‬
‫‪.‬‬
‫פתרון‪:‬‬
‫נגזור את הפונקציה‬
‫‪ y'  3x 2  4 x‬נציב את ערכי הנקודה ונקבל‬
‫‪y'  3 * 2 2  4 * 2  4‬‬
‫נמצא את משוואת המשיק בנקודה‬
‫) ‪y  y 0  m( x  x 0‬‬
‫)‪y  4  4( x  2‬‬
‫‪4x  y  4  0‬‬
‫ועכשיו משוואת הנורמל בנקודה‬
‫‪1‬‬
‫) ‪( x  x0‬‬
‫‪m‬‬
‫‪y  y0  ‬‬
‫‪1‬‬
‫)‪y  4   ( x  2‬‬
‫‪4‬‬
‫‪4 y  x  18  0‬‬
‫‪ .2‬באיזו נקודה של הפונקציה‬
‫א‪ .‬מקביל לישר‬
‫ב‪.‬‬
‫‪12 x  y  17‬‬
‫מאונך לישר‬
‫‪x  3y  2‬‬
‫א‪ .‬נגזור את הישר‬
‫נגזור את הפונקציה‬
‫‪ y  x 2  5‬המשיק‬
‫‪ 12  y'  0‬ומכאן‬
‫‪y'  12‬‬
‫‪ y'  2 x‬השיפוע של הישר המקביל ושל הפונקציה‬
‫בנקודת ההשקה זהים ולכן‬
‫נציב את ה ‪ x‬שקבלנו במשוואת הפונקציה‬
‫נקודת ההשקה היא‬
‫ומשוואת המשיק בנקודת ההשקה‬
‫‪2 x  12‬‬
‫‪x6‬‬
‫‪y  6 2  5  41‬‬
‫)‪P(6;41‬‬
‫)‪y  41  12( x  6‬‬
‫‪y  12 x  31  0‬‬
‫‪1‬‬
‫)‪( x  6‬‬
‫‪12‬‬
‫‪12 y  492   x  6‬‬
‫‪12 y  x  498  0‬‬
‫‪y  41  ‬‬
‫ומשוואת הנורמל תהיה‬
‫ב‪ .‬בכדי למצוא ישר מאונך לישר הנתון‬
‫‪1‬‬
‫‪3‬‬
‫נמצא את השיפוע ('‪ )y‬של הישר ‪x  3 y  2‬‬
‫ושיפוע המאונך לו יהיה‬
‫‪y'  ‬‬
‫‪y'  3‬‬
‫השיפוע של הישר המשיק ושל הפונקציה בנקודת ההשקה זהים ולכן‬
‫‪y'  2 x  3‬‬
‫נגזרת הפונקציה ‪ y'  2 x‬שווה לשיפוע הישר‬
‫נציב את ה ‪ x‬שקבלנו במשוואת הפונקציה‬
‫נקודת ההשקה היא‬
‫ומשוואת המשיק בנקודת ההשקה‬
‫‪x  1.5‬‬
‫‪y  x 2  5  1.5 2  5‬‬
‫)‪P(1.5;7.25‬‬
‫)‪y  7.25  3( x  1.5‬‬
‫‪3x  y  2.75  0‬‬