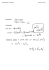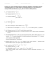MAA9.2 koe ja ratkaisut välivaiheineen (PDF)

MAA9.2
2014
Jussi Tyni
Lue ohjeet huolellisesti! Tee pisteytysruudukko konseptin yläkertaan. Muista
kirjoittaa nimesi. Kysymyspaperin saa pitää.
A-OSIO: Ei saa käyttää laskinta. MAOL saa olla esillä. Maksimissaan 1 h aikaa.
Palauta A-osion vastaukset valvojalle, jonka jälkeen voit ottaa laskimen esiin ja
siirtyä tekemään B-osiota. Valitse tehtävistä A1-A3 kaksi, joihin vastaat.
A1.
a) Laske lausekkeen
1

sin  3cos  tarkka arvo, kun 𝛼 = 𝜋.
2
2
b) Määritä vakio k siten, että jono, jolle 𝑎1 = 12 , 𝑎2 = 6 𝑗𝑎 𝑎3 =
geometrinen.
A2.
6
6p
a) Muunna radiaaneiksi −225°
b) Muunna asteiksi
4𝜋
9
c) Ratkaise yhtälö cos(4x) = -1
A3.
3𝑘−12
a) Derivoi funktio f (x) =
6p
cos x
.
sin x  1
𝜋
b) Derivoi funktio 𝑔(𝑥) = 𝑠𝑖𝑛 (2𝑥 + 4 ) ∙ 𝑐𝑜𝑠𝑥
6p
on
B-OSIO: Saa käyttää laskinta. MAOL saa olla esillä. Valitse tehtävistä B4-B8 neljä,
joihin vastaat. Bonustehtävä on vapaaehtoinen, sen saa tehdä jos huvittaa ja siitä
tulevat pisteet ovat vain plussaa.
B4.
a) Jonon kolme ensimmäistä jäsentä ovat 3, 7 ja 11. Monesko jonon jäsen on luku
3995?
b) Jonon kolme ensimmäistä jäsentä ovat 2, 5 ja 12,5. Määritä jonon 20 ensimmäisen
jäsenen summa.
6p
B5.
a) Bakteeriviljelmä lisääntyy 5,5 %:lla joka minuutti. Kello 14.00 viljelmässä laskettiin
olevan 1500 bakteeria. Paljonko viljelmässä on bakteereja klo 15.15?

𝜋

b) Ratkaise yhtälö cos (x + 3 ) = cos  x   .
2

B6.
x
+ cos x suurin ja pienin arvo suljetulla välillä
2
kolmen desimaalin tarkkuudella.
a) Määritä funktion f (x) =
6p
  
  2 , 2 
b) Kuinka monta aritmeettisen jonon 2, 8, 14, … jäsentä on laskettava yhteen, jotta
summa ylittäisi 120 000?
6p
B7.
Matin piti pinota 220 tiiltä kerroksittain niin, että toisesta kerroksesta ylöspäin
jokaisessa kerroksessa on yksi tiili vähemmän, kuin edellisessä, ja viimeisessä
kerroksessa on yksi tiili. Kuinka monta tiiltä Matti laittoi ensimmäiseen kerrokseen,
kun ylijäämätiiliä piti jäädä mahdollisimman vähän ? Kuinka monta tiiltä jäi yli?
6p
B8.
Asuntolaina, jonka suuruus oli 160 000 €, maksettiin takaisin 15 vuoden aikana niin,
että aina puolivuosittain maksettiin yhtä suuri lainan lyhennyserä. Samalla maksettiin
lainan korko edelliseltä puolelta vuodelta. Lainalle oli sovittu koko laina-ajalle kiinteä
3,8% vuosikorko. Kuinka paljon rahaa kului lainan korkojen maksuun?
6p
---------------------------------------------------------------------------------------------------------------------------------BONUS +2p:
Tutkimuksen mukaan erään metsälammen ahvenet lisääntyivät 3 % vuosivauhdilla,
mutta mökkiläiset kalastavat vuosittain n.2000 ahventa. Kuinka suuri on ahvenkanta
10 vuoden kuluttua, kun se on nyt arviolta 30 000 kpl?
RATKAISUT:
A1.
a) Laske lausekkeen
1

sin  3cos  tarkka arvo, kun 𝛼 = 𝜋.
2
2
1
𝜋
1
Jos 𝛼 = 𝜋, niin lauseke saa arvon 2 𝑠𝑖𝑛 2 + 3𝑐𝑜𝑠𝜋 = 2 ∙ 1 + 3 ∙ (−1) = −2,5
𝜋
𝑠𝑖𝑛 2 = 1
𝑐𝑜𝑠𝜋 = −1
b) Määritä vakio k siten, että jono, jolle 𝑎1 = 12 , 𝑎2 = 6 𝑗𝑎 𝑎3 =
3𝑘−12
6
on
geometrinen.
Jotta jono olisi geometrinen, seuraava jäsen saadaan edellisestä kertomalla
suhdeluvulla q. 12 ∙ 𝑞 = 6 ↔ 𝑞 = 0,5. Tällöin kolmas jäsen olisi 6 ∙ 0,5 = 3.
Nyt siis 3 =
3𝑘−12
6
‖ ∙ 6 ↔ 18 = 3𝑘 − 12 ↔ 30 = 3𝑘 ↔ 10 = 𝑘
K:n pitää siis olla 10, jotta jono olisi geometrinen.
A2.
𝜋
a) Muunna radiaaneiksi −225° = − 180° − 45° = −𝜋 − 4 = −
(toisaalta: −225° = 135° =
b) Muunna asteiksi
4𝜋
9
=
4∙180°
9
3𝜋
4
5𝜋
4
)
= 80°
c) Ratkaise yhtälö cos(4x) = -1
𝑐𝑜𝑠𝜋 = −1
 4𝑥 = 𝜋 + 2𝜋𝑛‖: 4 (vain yksi ratkaisu, koska cos ei voi olla muualla -1)
𝜋
2𝜋
𝜋
𝜋
 𝑥 = 4+ 4 𝑛 ↔ 𝑥 = 4+2𝑛
A3.
cos x
sin x  1
a) Derivoi funktio f (x) =
𝑓 ′ (𝑥) =
−𝑠𝑖𝑛𝑥∙(𝑠𝑖𝑛𝑥+1)−𝑐𝑜𝑠𝑥∙𝑐𝑜𝑠𝑥
−1(𝑠𝑖𝑛𝑥+1)
(𝑠𝑖𝑛𝑥+1)2
(𝑠𝑖𝑛𝑥+1)2
=
−𝑠𝑖𝑛2 𝑥−𝑠𝑖𝑛𝑥−𝑐𝑜𝑠2 𝑥
(𝑠𝑖𝑛𝑥+1)2
−1
=
−1(𝑠𝑖𝑛𝑥+𝑠𝑖𝑛2 𝑥+𝑐𝑜𝑠2 𝑥)
(𝑠𝑖𝑛𝑥+1)2
=
= 𝑠𝑖𝑛𝑥+1
𝜋
b) Derivoi funktio 𝑔(𝑥) = 𝑠𝑖𝑛 (2𝑥 + 4 ) ∙ 𝑐𝑜𝑠𝑥
𝜋
𝜋
𝜋
𝑔′ (𝑥) = 𝐷𝑠𝑖𝑛 (2𝑥 + 4 ) ∙ 𝑐𝑜𝑠𝑥 + 𝐷𝑐𝑜𝑠𝑥 ∙ 𝑠𝑖𝑛 (2𝑥 + 4 ) = 𝑐𝑜𝑠 (2𝑥 + 4 ) ∙ 2 ∙ 𝑐𝑜𝑠𝑥 +
𝜋
𝜋
𝜋
(−𝑠𝑖𝑛𝑥) ∙ 𝑠𝑖𝑛 (2𝑥 + ) = 2𝑐𝑜𝑠𝑥𝑐𝑜𝑠 (2𝑥 + ) − 𝑠𝑖𝑛𝑥𝑠𝑖𝑛 (2𝑥 + )
4
4
4
B4.
a)
d=4 => 𝑎𝑛 = 3 + (𝑛 − 1) ∙ 4 = 3995 ↔ 3 + 4𝑛 − 4 = 3995
4𝑛 − 1 = 3995
4𝑛 = 3996
𝑛 = 999
 Luku 3995 on 999. jäsen annetussa jonossa.
b) Jonon kolme ensimmäistä jäsentä ovat 2, 5 ja 12,5. Määritä jonon 20 ensimmäisen
jäsenen summa.
q=2,5 => 𝑆20 = 2
B5.
(1−2,520 )
1−2,5
= 121265958,9
a) Bakteeriviljelmä lisääntyy 5,5 %:lla joka minuutti. Kello 14.00 viljelmässä laskettiin
olevan 1500 bakteeria. Paljonko viljelmässä on bakteereja klo 15.15.
𝑆75 = 1500
(1−1,05575 )
1−1,055
= 1485114,6 ≈ 1485100 𝑏𝑎𝑘𝑡𝑒𝑒𝑟𝑖𝑎

𝜋

b) cos (x + 3 ) = cos  x   =>
2

𝜋
𝜋
𝜋
𝜋
𝑥 + 3 = 𝑥 − 2 + 2𝜋𝑛 ∨ 𝑥 + 3 = − (𝑥 − 2 ) + 2𝜋𝑛
𝜋
𝜋
𝜋
𝜋
0 = − 3 − 2 + 2𝜋𝑛 ∨ 2𝑥 = 2 − 3 + 2𝜋𝑛
𝜋
𝑒𝑖 𝑟𝑎𝑡𝑘𝑎𝑖𝑠𝑢𝑎 ∨ 2𝑥 = 6 + 2𝜋𝑛
𝜋
𝑒𝑖 𝑟𝑎𝑡𝑘𝑎𝑖𝑠𝑢𝑎 ∨ 𝑥 = 12 + 𝜋𝑛
B6.
x
+ cos x suurin ja pienin arvo suljetulla välillä
2
kolmen desimaalin tarkkuudella.
a) Määritä funktion f (x) =
𝑓 ′ (𝑥) =
1
√2
  
  2 , 2 
− 𝑠𝑖𝑛𝑥
Ääriarvot derivaatan nollakohdista tai tarkasteluvälin päätepisteistä:
1
√2
− 𝑠𝑖𝑛𝑥 = 0 ↔ 𝑠𝑖𝑛𝑥 =
𝜋
1
√2
𝜋
𝑥 = 4 + 2𝜋𝑛 ∨ 𝑥 = 𝜋 − 4 + 2𝜋𝑛 =
3𝜋
4
+ 2𝜋𝑛
𝜋
Annetulla suljetulla välillä on ainoastaan x:n arvo 𝑥 = 4 . Katsotaan merkkikaaviolla
kummasta ääriarvosta tässä on kysymys:
𝜋
4
f’(x)
-
+
f(x)
𝜋
1
𝑓 ′ (5) =
√2
𝜋
1
𝑓 ′ (3) =
√2
𝜋
− 𝑠𝑖𝑛 5 = 0,12
𝜋
− 𝑠𝑖𝑛 3 = −0,16
𝜋
Ollaan siis löydetty funktion f(x) suurin arvo, kun 𝑥 = 4 . =>
𝜋
𝑓 (4 ) =
𝜋
4
𝜋
√2
+ 𝑐𝑜𝑠 4 =
√2𝜋
8
+
1
√2
≈ 1,2625 on funktion suurin arvo.
Tarkastellaan vielä funktion arvoja suljetun välin päätepisteissä, jotta löydetään
pienin arvo:
𝜋
𝑓 (− 2 ) =
𝜋
𝑓 (2 ) =
−
𝜋
2
√2
𝜋
2
√2
𝜋
+ cos (− 2 ) = −
𝜋
+ cos (2 ) =
√2
𝜋
4
√2
𝜋
4
≈ −1.111
on siis pienin arvo!
≈ 1.111
b) d = 6, jäsenten määrä on tuntematon, merkitään n . Viimeinen jäsen on tällöin 𝑎𝑛 .
Aritmeettisen jonon n. jäsenen kaavaa käyttäen saadaan: 𝑎𝑛 = 𝑎1 + (𝑛 − 1) ∙ 𝑑 = 2 +
(𝑛 − 1)6 = 2 + 6𝑛 − 6 = 6𝑛 − 4. Eli jos tässä jonossa on n. kpl jäseniä, niin viimeinen jäsen
saadaan järjestysluvusta n laskien 6n-4.
Käytetään sinnikkäästi summan kaavaa, vaikka jäsenten lukumäärää ei tiedetä:
𝑆𝑛 = 𝑛
2+6𝑛−4
summan
2
pitää olla yli 120000, joten =>
𝑛
2 + 6𝑛 − 4
≥ 120000‖∙ 2
2
𝑛(2 + 6𝑛 − 4) = 240000
𝑛(6𝑛 − 2) = 240000
6𝑛2 − 2𝑛 − 240000 = 0
Toisen asteen yhtälö, josta ratkaisut:
𝑛 = 200,17 𝑡𝑎𝑖 𝑛 = −199,83
N on jonon jäsenten lukumäärä, mikä ei tietenkään voi olla negatiivinen, joten n = 200,17, eli
noin 201 jäsentä pitää laskea yhteen, jotta summaksi saadaan yli 120 000.
B7.
Kun ajatellaan tiilikasaa ylhäältä alaspäin, niin muodostuva jono on: 1, 2, 3, … , x, x, missä
kahta viimeistä (alinta) jäsentä ei tiedetä. Hoksasithan tehtävänannosta, että kahteen ekaan
(alimpaan ) riviin tulee saman verran tiiliä. Summan pitäisi siis olla seuraavanlainen:
𝒂𝟏 𝒂𝟐 𝒂𝟑
𝒂𝒏 𝒂𝒏+𝟏
1 + 2 + 3 + ⋯ + 𝑥 + 𝑥 ≤ 220
Nakataan tuo viimeinen x summan oikealle puolelle (jotta saadaan selkeä, looginen jono):
1 + 2 + 3 + ⋯ + 𝑥 ≤ 220 − 𝑥, missä meillä on nyt vasemmalla puolella koko ajan yhdellä
pykälällä kasvava aritmeettinen jono, missä d = 1 ja siinä on x=n kpl jäseniä.
Aritmeettisen jonon summa: 𝑆𝑛 = 𝑛
1+𝑛
2
= 220 − 𝑛‖∙ 2
𝑛(1 + 𝑛) = 440 − 2𝑛
𝑛 + 𝑛2 = 440 − 2𝑛
𝑛2 + 3𝑛 − 440 = 0
Toisen asteen yhtälö, jonka ratkaisut ovat: n = 19,53 tai n = -22,5. N kuvaa jonon termien
lukumäärä, ja se ei tietenkään voi olla negatiivinen, joten n = 19,53. Tiiliä pitää pinota 19
kerrosta + se yksi alin kerros , johon tulee saman verran tiiliä kuin toiseksi alimpaan = 20
kerrosta, jotta summa jää alle 220 kpl. Kokeillaan vielä laskea summa 19 kerrokselle tiiliä:
1+19
𝑆19 = 19 2 = 190. Alimpaan ja toiseksi alimpaan tulee 19 kpl, joten tähän pitää vielä
lisätä 19 tiiltä. Tiiliä on kasassa siis 209 kpl. Yli jää 11 tiiltä.
B8.
Asuntolaina, jonka suuruus oli 160 000 €, maksettiin takaisin 15 vuoden aikana niin,
että aina puolivuosittain maksettiin yhtä suuri lainan lyhennyserä. Samalla maksettiin
lainan korko edelliseltä puolelta vuodelta. Lainalle oli sovittu koko laina-ajalle kiinteä
3,8% vuosikorko. Kuinka paljon rahaa kului lainan korkojen maksuun?
Maksukertoja 30 kpl => Yksi maksuerä
16000
3
= 5333,33 €
Taulukoidaan maksukertoja:
1. 5333,33€ + 0,019 ∙ 160000
2. 5333,33€ + 0,019 ∙ 154666,66
3. 5333,33€ + 0,019 ∙ 149333,33
30. 5333,33€ + 0,019 ∙ 5333,33
Summataan nuo korkojen osuudet:
𝐾𝑜𝑟𝑘𝑜 𝐾 = 0,019 ∙ 160000 + 0,019 ∙ 154666,66 + 0,019 ∙ 149333,33 + ⋯
+ 0,019 ∙ 5333,33
= 0,019(160000 + 154666,66 + 149333,33 + ⋯ + 5333,33)
Sulkujen sisässä on nyt 30 jäsenen aritmeettinen summa, jossa 𝑑 =
Lasketaan sulkujen sisässä oleva summa: 𝑆30 = 30 ∙
16000
+160000
3
2
16000
3
= 5333,33
= 2480000
Nyt 𝐾 = 0,019 ∙ 2480000 = 47120€
----------------------------------------------------------------------------------------------------------------------------------BONUS +2 p
Ahventen lukumäärä on 1. vuonna 1,03∙30000 -2000 ja
toisena vuonna 1,03∙(1,03∙30000 – 2000) – 2000. = 1,032∙30000- 1,03∙2000 – 2000.
Kolmantena vuonna ahvenia on 1,03∙(1,032∙30000 – 1,03∙2000 -2000) -2000 =
1.033∙30000 – 1,032∙2000 – 1,03∙2000 – 2000. Samalla tavalla jatkamalla saadaan
ahvenpopulaatioksi 10 vuotena 1,0310∙30000 – 1,039∙2000 - … -1,03∙2000 - 2000. =
1,0310∙30000 -2000∙(1 + 1,03 + … + 1,039) = 1,0310∙30000 -2000∙
= 17389,7…≈ 17000.