Achieving Equal Loudness between Audio Files

Transcription

Achieving Equal Loudness
between Audio Files
Evaluation and improvements of loudness algorithms
PAUL
NYGREN
Master of Science Thesis
Stockholm, Sweden 2009
Achieving Equal Loudness
between Audio Files
Evaluation and improvements of loudness algorithms
PAUL
NYGREN
Master’s Thesis in Music Acoustics (30 ECTS credits)
at the School of Media Technology
Royal Institute of Technology year 2009
Supervisor at CSC was Svante Granqvist
Examiner was Sten Ternström
TRITA-CSC-E 2009:032
ISRN-KTH/CSC/E--09/032--SE
ISSN-1653-5715
Royal Institute of Technology
School of Computer Science and Communication
KTH CSC
SE-100 44 Stockholm, Sweden
URL: www.csc.kth.se
Achieving equal loudness between audio files
– Evaluation and improvements of loudness algorithms
Abstract
This master’s thesis presents the evaluation of several loudness calculation algorithms. Two of the algorithms are published standards: Replay Gain and ITU-R BS.
1770, and the others are modifications of these two. To evaluate the algorithms, a
loudness listening experiment was realized. In the experiment audio files containing
speech and pop music were used. The audio files and the corresponding subjective
loudness values retrieved from the experiment were used to evaluate the algorithms.
The precision of the algorithms was also tested using a subjective loudness database
from IRT (Institut für Rundfunktechnik). In both evaluations, ITU-R BS. 1770 produced lower errors than the Replay Gain algorithm, when compared to the subjective
loudness values. Of the modified algorithms, the ITU based algorithms that included
a gate function, produced the best result.
Att uppnå jämn hörstyrka mellan ljudfiler
– Utvärdering och förbättringar av hörstyrkealgoritmer
Sammanfattning
Detta examensarbete presenterar en utvärdering av flera hörstyrkeberäkningsalgoritmer. Två av algoritmerna är publicerade standarder: Replay Gain och ITU-R BS.
1770, och de andra är modifieringar av dessa två. För att kunna utvärdera algoritmerna så genomfördes ett lyssningsexperiment. I experimentet så användes ljudfiler
som innehöll tal och popmusik. Ljudfilerna och tillhörande subjektiva hörstyrkevärden från lyssningsexperimentet användes sedan för att utvärdera algoritmerna. Algoritmernas precision testades också med hjälp av en hörstyrkedatabas från IRT
(Institut für Rundfunktechnik). I båda utvärderingarna så gav ITU-R BS. 1770 lägre
fel än Replay Gain algoritmen, jämfört med de subjektiva hörstyrkevärdena. Av de
modifierade algoritmerna, så gav de ITU baserade algoritmerna som inkluderade en
”gate funktion” bäst resultat.
Recommendations to Swedish Radio
The conclusions from this project have led to these recommendations:
-
Change the loudness calculation method on audio files to ITU-R BS. 1770
-
Use ITU-R BS. 1770 together with a gate function for better precision.
-
Study if an adaptive gate function will give a more precise loudness calculation than a fixed gate function.
-
Study if another approach to can be used as a complement to the regular
audio file normalization process. One idea to a complement is what I call
“post normalization gain correction”. See chapter 6 for an explanation.
Table of contents
1. Introduction ................................................................................................. 1 1.1. Earlier work at Swedish Radio ............................................................................... 1 1.2. Purpose and method ............................................................................................... 2 1.3. Limitations ................................................................................................................ 2 1.4. Overview of the paper ............................................................................................ 2 2. Theory .......................................................................................................... 3 2.1. The auditory system................................................................................................. 3 2.2. Loudness ................................................................................................................... 3 2.3. Loudness level .......................................................................................................... 4 2.4. Critical bands ............................................................................................................ 5 2.5. Spectral effects.......................................................................................................... 5 2.6. Temporal effects ...................................................................................................... 7 2.7. Spatial effects............................................................................................................ 8 2.8. Gain normalization .................................................................................................. 8 2.9. Replay Gain............................................................................................................... 9 2.9.1. Original Version......................................................................................................... 9 2.9.2. Swedish Radio version ............................................................................................ 10 2.10. ITU-R BS. 1770...................................................................................................... 10 2.11. Algorithm modifications....................................................................................... 12 3. Method ....................................................................................................... 14 3.1. Evaluation using listening experiment database from Swedish Radio ........... 14 3.1.1. The loudness listening experiment at Swedish Radio....................................... 14 3.1.2. Evaluation method .................................................................................................. 18 3.2. Evaluation with loudness database from IRT ................................................... 20 3.2.1. Evaluation method ................................................................................................. 20 4. Results ........................................................................................................ 21 4.1. Results from the listening experiment at Swedish Radio ................................. 21 4.2. Results from the evaluation using loudness database from Swedish Radio.. 22 4.3. Results from the evaluation using loudness database from IRT..................... 25 5. Discussion .................................................................................................. 26 5.1. Listening experiment methodology..................................................................... 26 5.2. Listening experiment results................................................................................. 26 5.3. How good can an algorithm become? ................................................................ 28 6. Conclusions ................................................................................................ 29 7. Acknowledgements .................................................................................... 31 8. References .................................................................................................. 32 9. Appendix .................................................................................................... 34 Appendix A – Test subject listening level.............................................................................. 34 Appendix B – Audio file specifications .................................................................................. 35 Appendix C – Audio file histograms ...................................................................................... 36 Appendix D – Matlab code for the Replay Gain (Original) implementation .................. 40 Appendix E – Matlab code for the ITU-R BS. 1770 implementation .............................. 45 Appendix F – Matlab code for the ITU gate implementation............................................ 46 Appendix G – Matlab code for the ITU strongest section implementation.................... 48 Appendix H – Matlab code for the ITU with Replay Gain filter implementation .........50 Appendix I – Matlab code for the Replay Gain with ITU filter implementation ..........52 Appendix J – Matlab code for the RLB implementation .................................................... 54 Appendix K – Matlab code for the RLB gate implementation .......................................... 55 Appendix L – Matlab code for the regression analysis ........................................................ 57 Achieving equal loudness between audio files
1.
Introduction
For companies working with broadcasting, it is important to be able to keep an equal
perceived sound level, or equal loudness, between various programs and program
parts. Many people with different backgrounds, knowledge and preferences make the
programs, and in the current situation this would lead to major level differences if
program material for a whole day would be broadcasted without mixing. These differences would be annoying for the listeners, which would have to increase or decrease the volume every time the program content changes.
Nowadays, with a decreasing number of sound engineers working actively in the
productions and broadcasts, the number of people adjusting the incorrect levels is
getting fewer. For example, it is getting more and more common with what the
Swedish broadcast companies are calling “självkör” or “self-op” in English. This means
that one person can be working as a producer, host and sound engineer at the same
time in live broadcast. In a situation like this the person has no time, and probably
not the right education on how to adjust music and different program parts in level
so that they match each other. This is one of the reasons why broadcasting companies use different forms of process equipment to calculate and adjust sound levels on
audio files and live audio streams.
At Swedish Radio (SR) one process algorithm is used to calculate and adjust the
sound level on audio files ripped from audio CDs before the files are placed in the
audio database. Each audio file is adjusted with a single gain value. This
normalization process is used to achieve equal perceived sound level between the
different audio files in the database. The advantage with this adjustment is that it is
easier for both sound engineers and self-operators, which often have a very limited
time to listen through the music beforehand. The level differences between different
music pieces in broadcast will therefore decrease and a more equal loudness is
achieved.
The algorithm used at SR is called Replay Gain and is implemented in the software
AwaveSR, which is a company specific version of Awave Audio, developed by FMJsoftware (FMJ-software 2008). The algorithm is used on the music played in the popmusic oriented radio channels P3 and P4. According to several sound engineers at SR
the algorithm works well for most of the music that is played in P3 and P4, but of
course there are exceptions. After the normalization process, certain audio files still
have a perceived sound level that can differ from other music in the database by
more than 6 dB.
1.1.
Earlier work at Swedish Radio
In his master’s thesis, Matti Zemark (2007) presents a good overview of loudness
aspects in broadcast and gives suggestion on how to implement a standardized loudness measurement in all the steps of the broadcast production at SR. A new loudness
measurement algorithm is suggested, ITU-R BS. 1770, which also will be further
investigated in this thesis.
1
1.2.
Purpose and method
The purpose of this project is to evaluate the existing loudness calculation algorithm
Replay Gain, compare it to the standard suggested by the International
Telecommunication Union 2006, ITU-R BS. 1770 (ITU-R 2006), and also try to find
ways to improve the loudness calculation precision of the algorithms. An underlying
purpose is to investigate if it seems to be possible to use a normalization algorithm to
calculate loudness of audio files containing speech.
As a first step of the project relevant theory about psychoacoustics will be read. After
that an informal interview study with sound engineers and other personnel at SR will
be held to get initial knowledge of the specific conditions at SR and to get ideas for
how to improve the algorithms. The precision of Replay Gain, ITU-R BS. 1770, and
the new algorithm versions, will be measured using audio files and corresponding
subjective loudness data from a listening experiment that will be realized at SR. The
subjective data from the experiment will be compared to the values that the
algorithms give. The result from this evaluation will also be verified by a subjective
loudness database from IRT1.
1.3.
Limitations
This master’s project has its focus on the evaluation and improvement of loudness
calculation algorithms concerning whole audio files. The project will not evaluate and
analyze how the algorithms perform on real time audio streams.
Replay Gain is today used on audio files played in the pop music oriented channels
P3 and P4. Therefore the main focus in the evaluation part of this project is on pop
music. To evaluate and analyze the algorithms concerning the broad range of classical
music is beyond the scope of this project.
There are many aspects to take into account concerning the implementation of a
normalization process of speech material at Swedish Radio. This project will only
investigate how well the algorithms calculate loudness values of speech audio files.
1.4.
Overview of the paper
The first part of this master’s thesis is an introduction to relevant theory concerning
psychoacoustics and loudness. Gain normalization in general and the two loudness
algorithms are also described. Evaluation and analysis methods are described in the
next part of the thesis. The results are then presented, and after that a discussion
about methods and results are held. The thesis ends with the conclusions from the
evaluations and analysis of the algorithms.
IRT – Institut für Rundfunktechnik. A research institute for public-broadcasting organisations in
Germany, Austria and Switzerland (IRT 2009).
1
2
2.
Theory
This chapter is an introduction to the project area and is a summary of the literature study that was
made during the first part of the project.
2.1.
The auditory system
The auditory system will here be presented with focus on functions concerning loudness. For a deeper description see for example An introduction to the psychology of hearing
by Brian Moore (2003).
The outer, middle, and inner ear are the three main parts of the auditory system. The
pinna (the visual part of the ear) and the auditory canal form the outer ear. The pinna
works as a filter and affects the frequency content of incoming sound depending on
the direction of the sound, especially high frequency content. This helps us to localize sound sources (Moore 2003, p. 22). The auditory canal also affects the frequency
response of the auditory system because of its resonance at three kilohertz. The ear
therefore has extra sensitivity in this frequency region (Granqvist & Liljencrants
2004, p. 1-0). The function of the middle ear is to transfer incoming air born vibrations to liquid vibrations in the inner ear, with the assistance of the ear bones. Furthermore, the muscles of the ear bones can damp the transmission to protect the
inner ear from signals that is too great (Granqvist & Liljencrants 2004, p. 1-0). The
complicated structure of the inner ear consists among other things the cochlea where
the basilar membrane is located. The basilar membrane starts to oscillate when sound
is transferred through the auditory system in to the inner ear. The oscillation affects
the whole basilar membrane, but gets a maximum that is dependent on frequency
(Granqvist & Liljencrants 2004, p. 1-1). In the inner ear the oscillation is converted
to electrical impulses that reach the brain through nerve paths (Karolinska
Universitetssjukhuset 2009).
2.2.
Loudness
One of the abilities of the auditory system is to be able to order sounds from weak to
strong. Loudness, or “hörstyrka” in Swedish, is defined as that attribute of the auditory system. One problem concerning loudness is that it is a subjective entity, which
means that it can’t be measured directly (Moore 2003, p. 127). There are however
different ways to represent loudness. One is called “subjective loudness” (SL), and is
defined as “…the auditory sensation that allows us to order sounds on a scale from quiet to loud.
The loudness sensation may be described by either word labels or by numerical magnitude values.”
(Leijon 2007, p. 55). Another way is calculated loudness (CL). CL is defined as a
“…single number, based on physical sound measurements, such that the result can be assumed to
rank different sounds in the same order as the subjective loudness. The traditional unit of calculated
loudness is 1 sone, defined as the loudness of a pure 1000-Hz tone at 40 dB re 20 µPa.” (Leijon
2007, p. 55).
3
S.S. Stevens suggested one way to approximate the relation between physical intensity2 and loudness:
L = kI 0.3
(1)
where L is the loudness, I is the intensity, and k is a constant adapted to the units
used and to the subject. This approximation holds for sound levels over 40 dB
!
(Moore
2003, p. 132).
How the auditory system, and in the end the brain, does its analysis of how weak or
strong a sound is perceived is not entirely known. One assumption is that it is connected to the total neural activity raised by a specific sound (Moore 2003, p. 133).
2.3.
Loudness level
Barkhausen introduced the concept loudness level in the 20s (“hörnivå” in Swedish).
It was introduced to be able to make loudness comparisons between different
sounds. Zwicker and Fastl define the loudness level of a sound in their book
Psychoacoustics – Facts and Models (1999, p. 202) as “… the sound pressure level of a 1-kHz
tone in a plane wave and frontal incident that is as loud as the sound”. The unit is phon.
Loudness level can be measured for any sound, but most widely known are the
“Fletcher-Munson-curves”, see Figure 1, which shows the loudness level for
sinusoids (Zwicker & Fastl 1999, p. 203). The curves are based on tests made on
many American recruits (Granqvist & Liljencrants 2004, p. 1-7).
Figure 1 . The Fletcher-Munson-curves. Loudness level for sinusoids according to ISO standard (Granqvist &
Liljencrants 2004, p. 1-7).
It is interesting to note the effect of the ear canal resonance at 3 kHz, and the fact
that low frequency sinusoids needs a higher sound level to be perceived as loud as
middle and high frequency sinusoids.
If narrow band noise and a diffuse sound field are used instead of sinusoids the
curves change, see Figure 2.
Physical intensity – “…sound power transmitted through a given area in a sound field.” (Moore 2003, p.
402). One unit is W/m2.
2
4
Figure 2 . The change in loudness level with narrow band noise and a diffuse sound field (Granqvist & Liljencrants
2004, p. 1-7).
With loudness on a logarithmic vertical axis and loudness level on the horizontal axis
it can be seen that if the loudness level is raised by 9 phon, the loudness is doubled.
This rule is linear over approximately 40 phon.
Figure 3 . Loudness as a function of loudness level (Granqvist & Liljencrants 2004, p. 1-8).
2.4.
Critical bands
An important concept concerning loudness is the critical bands of the auditory system. It is a way to divide the frequency range of the ear in to different regions. This
makes it possible to calculate the loudness on wide band sounds by adding the loudness in each of the critical bands (Granqvist & Liljencrants 2004, p. 1-9). The frequency range is usually divided in to 25 regions with the unit Bark. Every “Bark” has
a center frequency and a bandwidth. The size of the bandwidth is dependent on the
center frequency. The bandwidth increases with higher center frequencies. One way
to determine the critical bandwidth at a certain center frequency is to let test subjects
listen to narrow band noise with a bandwidth that is gradually increased with a total
sound level that is constant. Up to a certain bandwidth the loudness will be perceived
as constant. When the loudness is perceived as higher than before, the critical bandwidth has been exceeded and consequently the critical band around a specific center
frequency can be determined (Granqvist & Liljencrants 2004, p. 1-9).
2.5.
Spectral effects
Different sounds have different spectrum. Certain sounds only have one frequency,
and other sounds have wide band spectrums. Zwicker and Fastl exemplify in their
book Psychoacoustics – Facts and Models one aspect of the loudness problems concerning that different sounds have different spectrum. For example, the loudness of 60
5
dB UEN3 is perceived approximately 3.5 times as loud than the loudness of a 1 kHz
sinusoid with the same physical sound pressure level. Therefore, the loudness is dependent on the width of the frequency content. Figure 4 illustrates the loudness difference between the 1 kHz sinusoid and the noise, which starts at the vertical dashed
line. The line coincides with the bandwidth of the critical band at 1 kHz for the
auditory system. If the bandwidth of the noise fits within a critical band, the loudness
increase mentioned above doesn’t appear. This is confirmed by similar measurement
at various center frequencies (Zwicker & Fastl 1999, p. 211).
Figure 4 . The sound level of a 1-kHz tone that is perceived as loud as band pass filtered noise at different
bandwidths. The total intensity of the noise is held constant (Zwicker & Fastl, 1999, p. 211).
A background noise can mask another sound, which also affects the loudness of
the sound. Figure 5 shows the loudness of a 1-kHz sinusoid as a function of its
sound pressure level. The dashed line corresponds to the loudness without the
noise, and the two lines correspond to the loudness with the masking noise. In this
case pink noise with a sound pressure level of 40 dB, and 60 dB per 1/3 octave
band.
Figure 5 . The loudness of a 1-kHz tone as a function of its sound pressure level. The dashed line corresponds to the
loudness without the noise and the two lines correspond to the loudness when a pink noise source with a sound pressure
level of 40 dB and 60 dB per 1/3 octave band is present (Zwicker & Fastl, 1999, p. 214).
UEN – Uniform exciting noise. White noise that has been filtered to give equal intensity in each
critical band (Zwicker & Fastl 1999, p. 170).
3
6
The masking of sounds is also dependent on how close the masking source is in
frequency to the other sound. In Figure 6, the loudness of a 60 dB sinusoid with a
varying frequency distance (∆f) to a high pass noise is illustrated. The high pass
noise has a cut-off frequency of 1-kHz and a sound pressure level of 65 dB in each
critical band. When ∆f is varied, the loudness of the tone is affected. If ∆f is getting
smaller, i.e. the sinusoid is getting close to the noise in frequency; the loudness of
the sinusoid is decreasing. The high pass noise will consequently decrease the loudness of the sinusoid, even if they are spectrally separated. Zwicker and Fastl writes
that these experiment result are important when modeling loudness (1999, p. 216).
Figure 6 . The loudness in sone for a sinusoid, when a high pass noise with a cut-off frequency of 1-kHz is present
at the same time, as a function of the distance between the sinusoid and the noise (Zwicker & Fastl, 1999, p. 215).
2.6.
Temporal effects
Most sounds vary over time, e.g. speech and music. This is why the temporal aspects
of sounds also are important for how humans perceive sound levels (Zwicker & Fastl
1999, p. 216). For example, a sinusoid with a length of 10 ms is perceived as weaker
than a similar sinusoid with the same sound pressure level, but with the length 100
ms. The length of a sound is affecting the loudness, and this is illustrated in Figure 7.
This feature of the auditory system is called “temporal integration” and holds up to
around 100 ms, and after that, the loudness of a sound is constant (Zwicker & Fastl
1999, p. 216). Moore (2003, p. 137) writes that extensive studies have been made on
the effects of temporal integration, but that the results are varying. The effect seem
to stop somewhere between 100-200 ms. Moore summarizes the measurements with
that up to approximately 80 ms, constant energy gives constant loudness.
Figure 7 . The loudness of a 2-kHz tone with a sound pressure level of 57 dB, as a function of the tone length in
milliseconds (Zwicker & Fastl, 1999, p. 216).
7
Another temporal effect that affects the loudness of a sound is masking sounds that
come before or after in time. Figure 8 shows loudness measurements when a 2-kHz
tone is played before noise (UEN). The tone is 5 ms long and has a sound level of
60 dB. ∆t is the distance in time between the tone and the masking noise. The
loudness will decrease when the distance between tone and masker decreases. The
implication of this is that even if the auditory system perceives the tone it takes
some time to create the impression of loudness. If the auditory system is disturbed
by another sound the impression of the earlier tone is interrupted (Zwicker & Fastl
1999, p. 219).
Figure 8 . The loudness of a 2-kHz tone that is played before noise, as a function of the distance between tone and
masker in milliseconds (Zwicker & Fastl, 1999, p. 219).
Something that also affects the loudness of a sound is if a person is exposed to high
sound levels a longer period of time. Eventually the hearing threshold will rise temporary. This effect can be measured right after a person has been exposed to the
sound and is called “temporary threshold shift” (Moore 2003, p. 146).
2.7.
Spatial effects
The filtering of the ear, depending of the direction of the sound, affects the perception of loudness. The fact that sound often reach the ears with a slight difference in
time also affects the loudness. This creates a complex phenomenon, e.g. when a
person listens to music with two loudspeakers in stereo, and is called “binaural loudness
summation”. The phenomenon can cause the perception of loudness with two loudspeakers to increase compared to one speaker when the both speaker systems are
playing at the same physical sound level (Skovenborg & Nielsen 2004, p. 3).
2.8.
Gain normalization
Normalization of audio files is a way to adjust the overall level of the files to match
each other by assigning a single gain to every file. There are many different methods
to normalize audio files. One way is to normalize the peak amplitude, i.e. find the
largest sample value in each file and adjust the overall gain so that the largest sample
in every audio file matches (Vickers 2001, p. 2). Another method is to measure the
mean level in the files and adjust them so that all files get the same mean level.
8
If equal loudness is the goal with the normalization, a weighting filter often is applied
before measuring the mean level in a file. This is done to give different frequencies
different weightings dependent on how loud the human ear perceives them
(Skovenborg & Nielsen 2004, p. 7).
2.9.
Replay Gain
2.9.1.
Original Version
Replay Gain is an open standard and is described on the website www.replaygain.org
(Replay Gain 2008). The algorithm was presented 2001, and the main idea is to calculate and store a value of the gain correction needed on an audio file to match the
perceived sound level of other audio files where the algorithm have been applied.
Replay Gain sets one gain correction value over a whole audio file, which for example could mean that the overall gain in a file could be adjusted with -10 dB.
There are two versions of Replay Gain; the first is called “Radio” Replay Gain and
works as the explanation above. The other one, “Audiophile” Replay Gain, calculates
the gain correction needed over a whole album, so that the intentional level differences within the album are left unchanged. In this thesis only “Radio” Replay Gain
will be described and evaluated.
The calculation process is divided into four steps, where the first is to filter the signal. The filter used is an inverted approximation of the Fletcher-Munson curves
(Replay Gain 2008), see Figure 9 for the filter target response.
Figure 9 . The target response for the Replay Gain filter, which is an inverted approximation of Fletcher-Munson
curves (Replay Gain, 2008).
Step two is to calculate the energy of the signal. The signal is divided into blocks of
50 milliseconds and the RMS4 energy is calculated over each block. Each value is
stored in an array. The energy of stereo files is calculated by adding the means of the
4
RMS – Root Mean Square.
9
two channels and divide by two before the square root is calculated. After the RMS
energy calculation, all values are converted into decibel.
The third step is to choose one RMS value from all the 50-millisecond blocks. Replay
Gain sorts all values into numerical order and picks the value that is stored 5 %
down in the array from the largest value.
The last step is to compare the calculated value with a reference. Replay Gain uses
pink noise with the RMS energy -20 dBFS5. The pink noise signal is sent through the
algorithm and the result is stored. Then the difference between the reference and the
audio file Replay Gain values is calculated, and this value is called the Replay Gain. In
Appendix D the Replay Gain algorithm is shown in Matlab code. The code is from
the website www.replaygain.org (Replay Gain 2008).
2.9.2.
Swedish Radio version
At SR, Replay Gain is implemented in the software AwaveSR. The difference between the original Replay Gain version and the one used in AwaveSR is the weighting filter. The frequency response of the AwaveSR filter together with the Replay
Gain original filter and the target response curve are shown in Figure 10.
Figure 10 . The weighting filter used in AwaveSR together with the Replay Gain original filter and target response.
2.10.
ITU-R BS. 1770
International Telecommunication Union (ITU) has suggested a standard for loudness
measurement (ITU-R 2006). The ITU document presents a way to measure loudness
for mono, stereo and multi-channel signals, and the suggested algorithm is a development of the Leq(RLB) algorithm.
RLB (Revised Low-frequency B-weighting) is a high-pass filter, and is a development
from the B-weighting curve, see Figure 11.
5
dBFS – Decibels relative to full scale. Used in digital systems with a maximum available level.
10
Figure 11 . The RLB weighting curve (ITU-R 2006, p.4).
The first stage of the algorithm is to apply a filter to account for the acoustic effects
of the head (ITU-R 2006, p. 4). The filter has a frequency response as shown in
Figure 12.
Figure 12 . The filter to account for the acoustic effects of the head (ITU-R
2006, p. 4).
The second stage is to filter the signal according to the RLB-weighting curve. The
two filters mentioned above is sometimes together named Leq(K) or Leq(R2LB) (Lund
2008, p. 3). After the filtering process the measurement is realized in two steps, and
the first is:
zi =
1
T
T
2
i
" y dt
(2)
0
where yi is the filtered input signal for channel i, and T is the interval of the measurement.
!
11
The other step is:
N
Loudness = "0.691+ 10log10 # Gi • zi
(3)
i=1
where Gi is a weighting coefficient for the different channels. For frontal channels Gi
equals 1 and for back channels 1.41. In Appendix E the implementation is shown in
! Matlab code.
2.11.
Algorithm modifications
During this project many different ITU and Replay Gain algorithm modifications
were tested. The ideas that these algorithms are based on, originate from discussions
with supervisors, sound engineers and other personnel at SR (except Center of Gravity).
In this thesis only the modified algorithms that produced low errors in relation to the
original algorithm versions are presented.
Center of Gravity – An ITU-R BS. 1770 implementation that includes an adaptive gate
function6. Described in the AES paper Loudness Descriptors to Characterize Programs and
Music Tracks by Esben Skovenborg and Thomas Lund (2008). (In this thesis only
tested using audio files and corresponding subjective loudness data from the SR listening experiment.)
ITU gate – An ITU-R BS. 1770 implementation with a fixed gate threshold value.
Different gate threshold values were tested, e.g. -70 dBFS. In Appendix F the implementation is shown in Matlab code.
ITU strongest section – An ITU-R BS. 1770 implementation, but instead of calculating
the RMS value over the whole file, the calculation was done over the strongest section. Different section sizes relative to the file length were tested, e.g. the strongest 5th
of each file. In Appendix G the implementation is shown in Matlab code.
ITU with Replay Gain filter – An ITU-R BS. 1770 implementation, but with the Replay
Gain filter instead. In Appendix H the implementation is shown in Matlab code.
Replay Gain with ITU filter – A Replay Gain implementation, but with the ITU
weighting instead. The difference from the original Replay Gain algorithm is shown
in Appendix I.
Replay Gain X ms – A Replay Gain implementation, but with a block length of X milliseconds instead of the standard 50 ms. In Appendix D the difference from the
Replay Gain (Original) algorithm is shown in a comment.
Replay Gain Y % – A Replay Gain implementation, but the value Y % down from the
maximum RMS value is chosen instead of the standard 5 %. In Appendix D the
difference from the Replay Gain (Original) algorithm is shown in a comment.
Gate function – A gate function disregards periods of audio with levels under a threshold value
during the loudness calculation. E.g. silence will be ignored.
6
12
RLB – An ITU-R BS. 1770 implementation, but without the 4 dB treble gain. The
Matlab implementation is shown in Appendix J.
RLB gate – As above, but with a fixed gate threshold value. Different gate threshold
values were tested, e.g. -70dBFS. The Matlab code is shown in Appendix K.
13
3.
Method
This chapter describes the evaluation and improvement methods used in the project.
To be able to evaluate the precision of the algorithms, audio files with corresponding
subjective loudness values collected from listening experiments were needed. The
audio files were run through the algorithms and the result was compared to the subjective loudness values from the listening experiments. An analysis with different
statistical measures was then realized, and the algorithm with the best precision from
the analysis would be considered to be the most accurate.
The algorithm ITU-R BS. 1770 and the Replay Gain (Original) algorithm were implemented in Matlab for the evaluation. The software AwaveSR was used to evaluate
Replay Gain (AwaveSR).
3.1.
Evaluation using listening experiment
database from Swedish Radio
3.1.1.
The loudness listening experiment at Swedish Radio
A loudness listening experiment was realized at SR to get a reference material to
evaluate the algorithms with. The test procedure was similar to the one that
Skovenborg et al. present in the paper Loudness Assessment of Music and Speech (2004). A
pair of audio files was presented to the test subject, the first one with a fixed sound
level and the second with an adjustable sound level. The task for the test subject was
to adjust the overall sound level of the second audio file so that it perceptually would
match the sound level of the first audio file. When the test subject was satisfied with
the adjustment, the level difference between the two audio files was stored and a new
pair of audio files was presented.
All audio files were normalized before they were used in the listening experiment and
the reason was to get a fairly equal listening level during the test. The normalization
procedure followed Skovenborg et al. (2004, pp. 4-5), but an RLB-weighted filter was
used instead of a B-weighted. The overall level in every audio file was adjusted so
that the (RLB-weighted) RMS value of each file matched the RMS value of a pink
noise filtered the same way. During the experiment, before each new level
adjustment, the second audio file in every pair also got a random level offset between
-6 dB and +6 dB to give each test subject different start level on the second audio
file. The gain change due to the normalization of each audio file were stored and
accounted for after each experiment so that the original level differences between all
matched pairs were stored.
The sound pressure level at the listening position was measured with the same pink
noise that was used for the normalization of the audio files. Before an experiment
started, each test subject had the possibility to adjust the mean listening level between
60 – 75 dB(C). Most of the test subjects preferred a listening level of 65 dB(C). In
Appendix A the listening level of each test subject is shown.
14
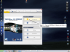
An interface was made in Pure Data7, see Figure 13, which controlled the listening
experiment. The interface was connected to a mixing console through MIDI8.
Figure 13 . The interface in Pure Data.
The test subjects controlled the interface with three faders and two mute buttons on
the mixing console. The mixing console is shown in Figure 14. The subjects could
choose to listen to one or both audio files at the same time, and also choose different
time positions in the files. One fader controlled the level of the second audio file and
the other two controlled the playback positions of the two audio files. By pressing
the buttons, the audio files could be muted. Before an experiment started, the test
subject got instructions and training on how the equipment and interface functioned.
The test equipment was set up and calibrated with the help of sound engineers at SR
and is shown and described in Table 1 and Figure 14 and 15 below. The
loudspeakers were placed 1.7 meter apart at a height of 1.0 meter and with a distance
of 2.4 meters from the listener.
Pure Data – A graphical programming environment for audio, video and graphical processing
(Pure Data 2009).
8 MIDI – Musical Instrument Digital Interface. (MIDI Manufacturers Association 2009)
7
15
Figure 14 . The interface controller unit. A digital mixing console connected to Pure Data through MIDI. The two
faders to the left controlled the playback positions of the two audio files. With the third fader (red colored), the level of the
second audio file was controlled.
Amplifier:
Audio D/A converter:
Computer:
Loudspeakers:
Mixing console:
Subwoofer:
Yamaha DSP-AX1
Grace design m902 (unbalanced analog outputs)
Macintosh Macbook 1.1
Chario Syntar 200
Yamaha 01V96
Martin Logan Descent
Ta ble 1. The test equipment list.
Figure 15 . The listening experiment setup.
16
The audio files used in the test were chosen from three categories:
1. Speech, recorded in a studio or with low background noise (this category is
called Speech).
2. Music, frequently played in the channels P3 and P4 (this category is called P3P4).
3. Music, spectrally different and/or dynamically changing, i.e. difficult to set
one general sound level (this category is called Hard).
Categories and test material were chosen in consultation with supervisors and sound
engineers at SR. The speech sounds were monophonic and collected from the internal audio database and edited to be approximately 30 seconds long. The music material was imported from CDs and all tracks were full-length and in stereo. See
Appendix B for a description of the audio files that were used in the listening experiment together with corresponding index.
The test material consisted of 24 audio files (7 speech files and 17 music tracks).
Every audio file occurred three times in the test as shown in Table 2, which implied
36 level adjustments for each test subject. Each category was matched against the
other two categories approximately the same amount of times. The vertical axis (A)
represents the index of the audio files with a fixed sound level, and the horizontal
axis (B) represents the index of the audio files with variable level. For example,
audio file #2 and #13 were matched to audio file #1 and audio file #1 was matched
to audio file #24. Because all audio files occurred with the same frequency in the test,
the possible bias due to a specific reference sound could be avoided (Skovenborg &
Nielsen 2004, p. 13). Also, before each test, the order of the 36 level adjustments was
randomized so that the pair matching sequence would be different for all the test
subjects.
Ta ble 2. How the audio files were paired in the test. The vertical axis represents the index of the audio files with a fix
sound level, and the horizontal axis represents the index of the audio files with variable level.
Half the test subjects did the listening experiment according to Table 2, and the other
half did the test the opposite way, i.e. the horizontal axis (B) represents the reference
17
sounds. This was done to avoid that the order of the two audio files in each matching
would influence the test result.
Sixteen test subjects participated in the test, all males. Eight of them were sound
engineers from SR and the other eight had either some form of audio technology
education or music education.
3.1.2.
Evaluation method
The resulting data from the listening experiment consisted of the difference in decibels between all the matched audio file pairs. The decibel difference between an
audio file with index i and an audio file with index j is called DL(i,j) (DifferenceLevel) by
Skovenborg et al. (2004). In the following chapters, the nomenclature used by
Skovenborg et al. (2004) is used where possible. Using all the DifferenceLevel values
from the 16 test subjects, regression analysis was used to obtain the SegmentLevel or
SL(i) values. The SegmentLevel values correspond to the subjective level of each of the
24 audio files used in the listening experiment. Regression analysis is a method to
analyze the relation between a response variable and one or many explanatory
variables (Nationalencyklopedin 2009). Shown below (eq. 4) are the equations that
formed the starting point for the regression analysis. The result from the regression
analysis is an estimate of the SL(i) values and is based on a least-squares error
solution (Skovenborg et al. 2004, p. 10). Appendix L contains the Matlab commands
used for the regression analysis.
DL(1,2)=1*SL(1) – 1*SL(2) + 0*SL(3) + … + 0*SL(24)
DL(2,3)=0*SL(1) + 1*SL(2) – 1*SL(3) + … + 0*SL(24)
.
.
.
DL(24,1)= –1*SL(1) + 0*SL(2) +0*SL(3) + … + 1*SL(24)
(4)
All 24 audio files were run through the algorithms and the results were stored. The
audio files used here were not normalized. Each algorithm assigned one value to each
audio file, which was compared to the 24 SegmentLevel values from the regression
analysis.
To avoid any constant difference between the algorithm values and the SegmentLevel
values, zero-order correction was added to all algorithm values. The formula used is
shown below:
ModelPr ediction(i) = ModelPr edictionuncal (i) "
N
1
# (ModelPr edictionuncal " SegmentLevel(i))
N i=1
(5)
where ModelPredictionuncal(i) is the algorithm value of the audio file with index i before
correction.
!
The difference between a predicted value from an algorithm and the corresponding
subjective value is named SegmentError(i).
SegmentError(i) = ModelPr ediction(i) " SegmentLevel(i)
18
!
(6)
In figure 16, the above-mentioned steps are shown schematically.
Algorithm predictions:
ModelPredictionuncal(i)
Listening experiment result:
DifferenceLevel(i,j)
Zero-order correction
Regression analysis
Zero-order corrected algorithm predictions:
ModelPrediction(i)
Regression analysis result:
SegmentLevel(i)
SegmentError(i)=ModelPrediction(i)-SegmentLevel(i)
Figure 16 . From listening experiment result and algorithm predictions to the SegmentError values.
Based on all SegmentError values five statistical measures were calculated:
Average Absolute Error (AAE) – the absolute mean of all SegmentError values for one
algorithm.
AAE =
1 N
" SegmentError(i)
N i=1
(7)
Absolute Standard Deviation (ASD) – the absolute standard deviation of all SegmentError
values for one algorithm.
!
ASD =
1
N
N
! ( SegmentError (i) " AAE )
2
(8)
i =1
Maximum error (MaxError) – the maximum error that an algorithm made when
comparing all SegmentLevel values.
Root Mean Square Error (RMSE) – the root mean square of the SegmentError values.
Gives more weight to the high errors (Skovenborg & Nielsen 2004, p. 17).
RMSE =
1 N
" SegmentError(i) 2
N i=1
(9)
!
19
95th Percentile Absolute Error (P95AE) – The value that 95 % of the absolute
SegmentError values are below.
Using the first results from the listening experiment as a starting point, explanations
for the differences between the algorithm values and the subjective listening experiment results were searched. Among other things amplitude histograms of the audio
files were plotted and analyzed. An amplitude histogram displays how the levels in an
audio file are distributed. The histograms are shown in Appendix C. The first results
were also used in the development process of the different algorithm modifications
described in section 2.12.
3.2.
Evaluation with loudness database from
IRT
At IRT, a loudness listening experiment has been realized. The loudness database
consisted of many audio segments, both speech and music, recorded from German
radio broadcasts. The segments were short, about 10-15 seconds and included several
music genres, such as: choral music, classical music, pop and metal. The speech segments consisted of male and female voices in different broadcast environments. Fifteen test subjects participated in the listening experiment. The result and audio segments from this listening experiment have been used to evaluate the algorithms in
this project.
3.2.1.
Evaluation method
From the IRT database, 68 audio segments were used to evaluate the algorithms. The
algorithms calculated and assigned loudness values for the audio segments and these
values were compared to the IRT database values using the same procedure as described in section 3.1.2, but no regression analysis was made since the database consisted of SegmentLevel values for all audio segments.
20
4.
Results
The result from the listening experiment at SR and from the two algorithm evaluations is presented
with the help of graphs and the five statistical measures described in section 3.1.2.
4.1.
Results from the listening experiment at
Swedish Radio
In Figure 17 the mean value and standard deviation of the 36 DifferenceLevel values for
the 16 test subjects in the listening experiment are shown. Every matching included a
pair of audio files. In this figure, Index of the audio files (i,j) corresponds to a specific
pair of audio files, see Appendix B for a description of the files.
Figure 17 . Mean and standard deviation of the DifferenceLevel values for the 16 test subjects for each matching in
the listening experiment.
21
4.2.
Results from the evaluation using
loudness database from Swedish Radio
In Table 3 and 4 the statistical measures from the first algorithm evaluation are presented. The subjective reference data is from the listening experiment at Swedish
Radio. Table 3 shows the results of the original algorithm versions.
ITU-R BS. 1770
Replay Gain (Original)
Replay Gain (AwaveSR)
AAE
1,04
1,18
1,35
ASD
0,69
0,77
0,96
MaxError RMSE
2,24
1,25
2,68
1,41
3,90
1,66
P95AE
2,17
2,67
3,28
Ta ble 3. ITU-R BS. 1770, Replay Gain (Original) and Replay Gain (AwaveSR) evaluated with the reference data
from the listening experiment at Swedish Radio. All measure units are in dB.
Table 4 shows the results of the modified algorithm versions. If several parameter
values of an algorithm version produced low errors in the evaluations, only the three
best parameter values of that algorithm version are presented here.
Center of Gravity
ITU gate (-60 dBFS)
ITU strongest 6th
ITU strongest 5th
ITU gate (-70 dBFS)
ITU gate (-63 dBFS)
Replay Gain 15%
Replay Gain 10 %
RLB gate (-60 dBFS)
RLB gate (-70 dBFS)
RLB gate (-65 dBFS)
RLB
ITU strongest 7th
Replay Gain 20%
Replay Gain 120ms
ITU with RG filter
Replay Gain with ITU filter
Replay Gain 150ms
Replay Gain 100ms
AAE
0,98
1,00
1,00
1,00
1,01
1,01
1,01
1,01
1,02
1,03
1,03
1,04
1,04
1,05
1,06
1,06
1,08
1,11
1,13
ASD
0,64
0,64
0,78
0,80
0,63
0,63
0,68
0,70
0,61
0,59
0,59
0,66
0,77
0,76
0,84
0,86
0,86
0,82
0,79
MaxError RMSE
2,32
1,17
2,48
1,19
3,14
1,27
3,31
1,28
2,40
1,19
2,45
1,19
2,96
1,22
2,91
1,23
2,15
1,19
2,11
1,18
2,15
1,19
2,30
1,23
3,18
1,30
2,99
1,3
2,65
1,35
2,91
1,36
3,54
1,39
2,80
1,38
2,65
1,38
P95AE
1,97
1,95
2,44
2,55
1,87
1,92
2,34
2,12
2,03
2,03
2,04
2,03
2,29
2,42
2,60
2,57
2,78
2,54
2,59
Ta ble 4. The results of the modified algorithm versions. All measure units are in dB.
In Figure 18 and 19 all 24 SegmentLevel values are shown together with ModelPrediction
values from eight of the above-mentioned algorithms. Three of them are the original
algorithm versions and the other five are chosen for their overall good performance
when considering all five statistical measures. A description of the audio files can be
found in Appendix B.
22
Figure 18 . The subjective loudness values (SegmentLevel values) of audio file 1-12 from the regression analysis
together with corresponding algorithm predictions.
23
Figure 19 . The subjective loudness values (SegmentLevel values) of audio file 13-24 from the regression analysis
together with corresponding algorithm predictions.
24
4.3.
Results from the evaluation using
loudness database from IRT
In Table 5 and 6 the statistical measures from the second algorithm evaluation are
presented. The subjective reference data is from IRT. Table 5 shows the results of
the original algorithm versions.
ITU-R BS. 1770
Replay Gain (Original)
Replay Gain (AwaveSR)
AAE
1,27
1,52
1,86
ASD
1,05
1,37
1,67
MaxError RMSE
5,23
1,65
6,15
2,04
8,86
2,50
P95AE
3,23
4,59
5,40
Ta ble 5. Replay Gain (AwaveSR), Replay Gain (Original) and ITU-R BS. 1770 evaluated with the reference data
from IRT. All measure units are in dB.
Table 6 shows the results of the modified algorithm versions. If several parameter
values of an algorithm version produced low errors in the evaluations, only the three
best parameter values of that algorithm version are presented here.
RLB gate (-50 dBFS)
ITU strongest 5th
RLB gate (-60 dBFS)
RLB gate (-65 dBFS)
ITU gate (-20 dBFS)
RLB
ITU gate (-50 dBFS)
ITU gate (-60 dBFS)
Replay Gain with ITU filter
Replay Gain 25%
Replay Gain 20%
Replay Gain 15%
ITU with Replay Gain filter
ITU strongest 6th
ITU strongest 7th
Replay Gain 80ms
Replay Gain 100ms
Replay Gain 120ms
AAE
1,15
1,15
1,15
1,16
1,18
1,18
1,22
1,24
1,33
1,42
1,39
1,44
1,45
1,48
1,50
1,54
1,54
1,61
ASD
1,06
1,07
1,07
1,06
1,01
1,05
1,05
1,05
1,20
1,39
1,44
1,37
1,31
1,26
1,31
1,45
1,50
1,51
MaxError RMSE
4,59
1,56
4,70
1,57
4,82
1,57
4,88
1,57
4,34
1,55
4,80
1,58
5,06
1,61
5,28
1,63
5,00
1,79
6,25
1,98
6,41
2,00
6,53
2,04
5,60
1,96
5,66
1,94
5,76
1,99
5,88
2,11
5,98
2,15
6,27
2,21
P95AE
3,43
3,40
3,36
3,34
3,23
3,27
3,04
3,06
3,74
4,40
4,85
4,97
4,29
3,62
3,92
4,74
5,14
5,35
Ta ble 6. The modified algorithms that produced an equal or lower AAE compared to ITU-R BS. 1770. All
measure units are in dB.
25
5.
Discussion
In the following chapter several aspects concerning the project methodology and results are discussed.
5.1.
Listening experiment methodology
When realizing a listening experiment it is always difficult to know if the test actually
will test the specific thesis or question that you have. There are many bias factors that
can influence your test and it might be difficult to draw any conclusions. In the listening experiment at SR several aspects concerning the methodology can be challenged, e.g.: Was the audio files to long? Was it good to let the test subjects choose
their own listening level? Was it a good choice to use a subwoofer? Was the mixing
console in the listening experiment a useable interface for the test subjects?
All these questions are relevant and can be discussed for a long time. The aim with
the listening experiment methodology was to try to simulate what the Replay Gain
algorithm is used for at SR and to let the test subjects use an interface that was intuitive to use. Using a fader as the level adjuster was considered to be the best way to
control the level, since a fader is the standard tool for a sound engineer when working with level adjustments. Replay Gain calculates one loudness value of a whole
audio file, and at SR most audio files that AwaveSR processes are imported from
CDs, with a length of 3-5 minutes in general. To simulate this, full-length music files
were used in the listening experiment. When sound engineers mixes live or recorded
audio in a studio they choose their own listening level. This is also the reason why
the test subjects could choose the reference level in the experiment. Whether the test
setup should have included a subwoofer or not is a complex question. If not, the test
result would probably be different, since the test subjects would have had different
sensations of the bass content in the audio files, but would it be more accurate? The
best way might have been to have two speaker setups and to let the test subjects do
the test twice and analyze the differences, but this was not possible due to time limitation.
In Figure 17 the mean value and standard deviation of each matching in the listening
experiment is shown. If the standard deviations would have been too large one could
have assumed that the listening experiment method was impracticable, but most of
the test subjects seem to agree fairly well on the gain adjustment between each audio
pair. The exceptions will be discussed in section 5.2.
In Loudness Assessment of Music and Speech, Skovenborg et al. (2004) model their listening experiment data with a General Linear Model (GLM), which included both regression analysis and an analysis of covariance. The authors also include several bias
factors in the model to try to reduce the influence of possible biases. In this project
only the regression analysis has been made. A deeper statistical analysis would
probably improve the validity of the data from the listening experiment.
5.2.
Listening experiment results
When analyzing the mean errors from the evaluations, both ITU-R BS. 1770 and
AwaveSR seem to match the mean subjective loudness values from the regression
26
analysis pretty well with ITU-R BS. 1770 having an AAE of 1.0 dB using the SR
subjective loudness data, and an AAE of 1.3 dB using the IRT subjective loudness
data. AwaveSR produces higher AAE values, but is not clearly worse. The biggest
difference between the ITU standard and AwaveSR is the maximum error, which is
considerably higher for AwaveSR, with a MaxError that is 1.7 dB (SR database) and
3.6 dB (IRT database) higher than the ITU standard.
When comparing Replay Gain (AwaveSR) and Replay Gain (Original), the second of
the two produced lower errors in both evaluations. The filter differences are mainly
in the bass region, and in Figure 10 it can be seen that the Replay Gain (Original)
filter is closer to the target response in the bass region (<200 Hz) than Replay Gain
(AwaveSR).
The modified algorithms that produced the lowest AAE in both the evaluations are
the ITU based ones that included a gate function. The ITU strongest 5th algorithm also
gave low AAE values in both evaluation but produced higher MaxError and P95AE
in the SR evaluation. It can also be discussed whether ITU strongest 5th can be evaluated using the IRT database since the length of the audio files are 10-15 seconds. To
calculate the loudness value over only 2-3 seconds of the file might not be a representative loudness value for the strongest section of a full-length audio file.
Many of the modified ITU versions that included a gate function produced low errors, but when comparing both evaluations, a single best gate threshold value could
not be found. This finding is confirmed in the paper Loudness Descriptors to Characterize
Programs and Music Tracks written by Skovenborg and Lund (2008, p. 2), where the
authors suggest an adaptive gate function instead of a fixed gate threshold.
One pattern can be seen when analyzing the mean value and standard deviation of
each pair-matching, see Figure 17. The standard deviation is higher when a speech
file is present. It can be discussed whether this is because balancing speech in general
is more difficult than to balance other audio material, or if the individual preferred
level difference between speech and music is the main cause. I believe that both
these explanations have affected the experiment result. In Appendix C the amplitude
histograms of the 24 audio files are shown. The music files have a much narrower
distribution of levels, and this can perhaps explain why the music files were easier to
balance than the speech files, but I also believe that there is a much larger, what
Skovenborg et al. (2004, p. 7) call, “between-subject disagreement” between music and
speech than it is between different pop music audio files. Different listeners prefer
different levels when listening to speech. Of course, the frequency spectrums of the
different audio files also affect the result that an algorithm produces. In the SR listening experiment the P3-P4 music all have quite similar spectrums, compared to the
two other categories speech and hard, where the frequency spectrums varies much
more. It seems to be easier to match audio files with similar spectrums, but more
exactly how different frequency spectrums affect the loudness calculation of an algorithm has not been closely studied in this project.
Concerning the number of audio files in the listening experiment at SR, one thing
must be noted. Since the number of audio files was low, an algorithm modification
that decreased the maximum error considerably, but maybe increased the mean error
of the other loudness predictions, could seem to be just as accurate to an algorithm
27
that has a lower mean error except for one really bad loudness prediction. The question is if it is better to have an algorithm that has a low mean error and few very bad
exceptions in the loudness predictions or the other way around? From my point of
view a low mean error is preferable in an audio file normalization process, since it
probably will be easier to locate and correct a few bad exceptions in the database.
The underlying purpose of this thesis was to investigate if it was possible to use a
normalization algorithm on audio files containing speech. This seems to be possible
after analyzing the results. All ITU based algorithms predicted the loudness fairly
well of the speech material available compared to the subjective references. When
comparing ITU-R BS. 1770 with Replay Gain (AwaveSR) and Replay Gain (Original)
concerning only the speech material, the ITU standard was closest to the subjective
reference data and Replay Gain (AwaveSR) did the worst loudness predictions. With
the data from the listening test at SR, the three worst loudness predictions from
Replay Gain (AwaveSR) are on speech material. When analyzing the results from the
evaluation with the subjective loudness database from IRT the same pattern can be
seen.
5.3.
How good can an algorithm become?
The result in this thesis indicates that many of the investigated algorithm versions
can produce good results, but the algorithms investigated here are probably not optimal. Neither Replay Gain, nor ITU-R BS. 1770 use an advanced, research based
loudness calculation model, which might improve the prediction of the algorithms.
On the other hand, Skovenborg and Nielsen (2004) investigated many loudness calculation algorithms and one of the findings was that several well-known models,
such as Leq(A) and the ISO 532-B implementation of a model suggested by Zwicker,
did not predict the loudness of music and speech satisfactorily. The predecessor to
the ITU standard, Leq(RLB), produced lower errors than both these two models. So it
is not obvious that a more advanced model would give a better algorithm.
With audio files and corresponding subjective loudness values retrieved from listening experiments, loudness algorithms can be optimized to match the subjective reference data in the best possible way, and this has also been done during this project.
The problem is that the optimization is done with very limited amount of data. There
is no guarantee that an “optimized algorithm” will be the best choice when using it
on other audio material.
Loudness calculation models, such as the ones used in Replay Gain and ITU-R BS.
1770, will never be good at predicting loudness for all audio material available. A
possible improvement might be to implement what Zemark (2007, p. 46) calls a
“category meter”, which would classify the audio material, for example into pop music,
classical music and speech, and after that perhaps use different loudness calculation
methods adapted to the different groups of audio material.
As a summary I believe that it is impossible to switch from having sound engineers
in the production chain to only use an automated audio file normalization process
without noticing any difference. But as a complementary tool, an audio file normalization process is a good way to facilitate for sound engineers and especially the selfoperators.
28
6.
Conclusions
In this master’s project several loudness calculation algorithms have been evaluated.
Two of them were published standards, Replay Gain and ITU-R BS. 1770, and the
others were modifications of these two. The algorithms were evaluated using two
subjective loudness databases. One was retrieved from a listening experiment realized
at Swedish Radio during the project, and the other one came from the research institute IRT. In both evaluations ITU-R BS. 1770 produced lower error than Replay
Gain. Of the modified algorithms, the ITU-based with gate function produced the
best result. Most of the gate threshold values tested produced slightly better result
than the ITU standard. A gate function seems to increase the precision of algorithms
that is based on mean level measurement, but when comparing the result from the
two evaluations, no single best gate threshold value could be found.
Concerning speech files, the ITU standard and modifications based on the ITU
standard, predicted loudness fairly well on the speech material available compared to
the subjective references. This indicates that it seems to be possible for SR to use a
similar normalization algorithm to adjust the overall level also on speech files in the
future.
The best choice for the audio file normalization process at Swedish Radio seems to
be an ITU-based loudness calculation algorithm together with a gate function. The
reason for this is not only based on the result from the evaluations made during this
project, but also because ITU-R BS. 1770 is a suggested professional loudness measurement standard. Such a standard will probably be tested, evaluated and also criticized by many different research groups and companies. The Replay Gain algorithm
is also a suggested standard, but developed by one person and not thoroughly evaluated. If a new better loudness calculation method is found in the future, it will
probably be tested against the ITU standard, but probably not against Replay Gain.
To choose an algorithm based on the ITU standard is considered by the author to be
a better choice than to stay with the Replay Gain algorithm, if Swedish Radio wants
to continue to follow the research concerning loudness calculation algorithms.
To investigate loudness calculation algorithms further, many different areas can be
studied. One area that connects closely to this project is to study if an adaptive gate
function will increase the precision of the ITU-R BS. 1770 algorithm compared to a
fixed gate function. An optimal fixed gate level threshold could not be found in this
project and this is why it would be interesting to see how an adaptive gate would
perform compared to a fixed gate level threshold. One ITU implementation with an
adaptive gate function was tested during this project, Center of Gravity (Skovenborg &
Lund 2008), but only using the loudness database from SR. The results seem promising, and this is why it would be interesting to continue to study different gate functions.
Another aspect to study is if a different approach can be used as a complement to
the audio file normalization process used today at SR. One idea to a complement is
what I call “post normalization gain correction”. If an audio file is detected that has considerably different subjective sound level than other audio files, sound engineers
should have the possibility to adjust the level of the file in the database. This could
29
also be automated by logging the lists of music played together with fader movements and time synchronization. If several sound engineers do (approximately) the
same level adjustment of an audio file, the level of the file should be adjusted.
30
7.
Acknowledgements
There are many people who have helped me during this project. I would like to
thank:
-
My supervisor at Swedish Radio: Christofer Bustad. For always helping out
with my theoretical and practical questions, for giving feedback and for putting so much time into the project.
-
My supervisor at Royal Institute of Technology: Ph.D. Svante Granqvist. For
giving feedback and for helping me with my questions concerning theory, my
report and the examination process.
-
Swedish Radio Production & Technical Development staff: Lars Jonsson,
Lars Mossberg, Bo Ternström and Hasse Wessman. For all help and support
during the project.
-
HD development manager Thomas Lund and Ph.D., Senior Research
Engineer Esben Skovenborg at TC Electronics. For hospitality, feedback and
interesting input to the project.
-
Dipl. -Ing. Gerhard Spikofski at IRT. For letting me use the subjective loudness database from IRT.
-
Software engineer Markus Dimdal, FMJ-Software. For answering my questions about AwaveSR and for giving me access to the source code of the
filter.
-
The listening experiment participants. Without you, no project!
-
My wife Anna for supporting and believing in me and for being a remembrance of the really important things in life.
31
8.
References
FMJ-Software (2008). FMJ-Software. (Online). Available: <http://www.fmjsoft.com>
(Accessed 2008-10-01).
Granqvist, S. & Liljencrants, J. (2004). Kompendium i Elektroakustik. Stockholm: Royal
Institute of Technology.
IRT (2009). IRT (Online). Available: <http://www.irt.de/en/irt.html>
(Accessed 2009-01-26).
ITU-R (2006). Rec, ITU-R BS. 1770-1, Algorithms to measure audio programme loudness
and true-peak audio level. International Telecommunication Union.
Karolinska Universitetssjukhuset (2009). Örats funktion. (Online). Available:
<http://www.karolinska.se/templates/Page____55847.aspx>
(Accessed 2009-01-28).
Leijon, A. (2007). Sound Perception: Introduction and Exercise Problems. Stockholm: Royal
Institute of Technology.
Lund, T. (2008). Inter-program level jumps in broadcast. Conference article from
”Broadcast Asia 2008”, 17-20 June 2008, Singapore.
MIDI Manufacturers Association (2009). Tutorial – MIDI and Music Synthesis.
(Online). Available: <http://www.midi.org/aboutmidi/tut_midimusicsynth.php>
(Accessed 2009-02-28).
Moore, B. (2003). An Introduction to the Psychology of Hearing. Great Britain: Academic
Press.
Nationalencyklopedin (2009). Regressionsanalys. (Online). Available:
<http://www.ne.se/artikel/291872> (Accessed 2009-01-28).
Pure Data (2009). Pure Data. (Online). Available: <http://puredata.info/>
(Accessed 2009-02-23).
Replay Gain (2008). Replay Gain – A Proposed Standard. (Online). Available:
<http://www.replaygain.org/> (Accessed 2008-09-10).
Skovenborg, E. & Lund, T. (2008). Loudness Descriptors to Characterize Programs and
Music Tracks. In Proc. of the AES 125th Convention, San Francisco.
32
Skovenborg, E. & Nielsen, S.H. (2004). Evaluation of Different Loudness Models with
Music and Speech material. In Proc. of the 117th AES Convention, San Francisco.
Skovenborg, E., Quesnel, R., & Nielsen, S.H. (2004). Loudness Assessment of Music and
Speech. In Proc. of the 116th AES Convention, Berlin.
Vickers, E. (2001). Automatic Long-term Loudness and Dynamics Matching. In Proc. of the
111th AES Convention, New York.
Zemark, M. (2007). Implementing methods for equal Loudness in Broadcasting at Swedish
Radio. Master of Science Thesis. Stockholm: Royal Institute of Technology.
Zwicker, E. & Fastl, H. (1999). Psychoacoustics: Facts and Models. Berlin: Springer.
33
9.
Appendix
Appendix A – Test subject listening level
Test subject Mean sound level at listener position, dB(C) (measured with pink noise)
1
60
2
65
3
65
4
65
5
65
6
65
7
65
8
65
9
65
10
65
11
60,5
12
66
13
66
14
60,5
15
70
16
61,5
34
Appendix B – Audio file specifications
The audio files used in the test were chosen from three categories:
1. Speech, recorded in a studio or with low background noise (Speech)
2. Music, frequently played in the channels P3 and P4 (P3-P4)
3. Music, spectrally different and/or dynamically changing, i.e. difficult to set
one general sound level (Hard)
Index
1
2
Category Audio file information (if from CD: Title, Artist, Record)
Alla vill till himmelen men ingen vill dö, Timbuktu, Alla vill till himmelen men
P3-P4
ingen vill dö
Speech Female voice (studio)
3
Hard
You raise me up, Josh Groban, Closer
4
P3-P4
Bills bills bills, Destiny's child, Bills bills bills
5
P3-P4
Viva la Vida, Coldplay, Viva la vida or death and his friends
6
Speech
Male voice (studio)
7
Speech
Female voices (treble dominated)
8
P3-P4
With Every Heartbeat, Kleerup feat. Robyn, Kleerup
9
Speech
Female voice (background noise)
10
P3-P4
Beautiful mourning, Machine Head, The blackening
11
Hard
My heart will go on, Celine Dion, My heart will go on
12
Hard
I will find you there, Michael Ruff, Speaking in melodies
13
Hard
Tennessee Waltz, Alma Cogan, Alma Cogan
14
Speech
Male voice (telephone)
15
P3-P4
Curly Sue, Takida, Bury the lies
16
P3-P4
Du Hast, Rammstein, Sehnsucht
17
Hard
Peach Blossom Spring, Yutaka Yokokura, Yutaka
18
Speech
19
Hard
Nightshift, The Commondores, Nightshift
20
Hard
Somliga går med trasiga skor, Cornelis Wreeswijk, Mäster Cees memoarer (2)
21
Speech
Male voice (studio)
22
P3-P4
Ligga lågt, Tomas Andersson Wij, Blues från Sverige
23
Hard
24
P3-P4
Killing me softly, The Fugees, The score
Cotton fields back home, Creedence Clearwater Revival, Willy and the poor
boys
Male voices (Sport interview)
35
Appendix C – Audio file histograms
(Before the amplitude histograms were calculated, any DC offset was removed)
Audio file #1 (P3-P4)
Audio file #2 (Speech)
Audio file #3 (Hard)
36
37
38
39
Appendix D – Matlab code for the Replay Gain
(Original) implementation
The code is from the website www.replaygain.org (Replay Gain 2008).
%
%
%
%
%
replaygainscript
Asks user for name of wavefiles (or folders containing
wavefiles)
User gives null response to indicate all files entered
Calculates replay gain of file using "replaygain" function
% To enter entire folder, append / or \ (i.e. "maskers/"
% processes all files in directory "maskers")
% David Robinson, July 2001. http://www.David.Robinson.org/
clear Vrms filenamematrix
% Get filter co-efs for 44100 kkHz Equal Loudness Filter
%- (IN MY THESIS 48000HZ WAS USED INSTEAD)
%- //Paul Nygren, 2009-02-24
[a1,b1,a2,b2]=equalloudfilt(44100);
% Calculate perceived loudness of -20dB FS RMS pink noise
% This is the SMPTE reference signal. It calibrates to:
% 0dB on a studio meter / mixing desk
% 83dB SPL in a listening environment (THIS IS WHAT WE'RE
% USING HERE)
[ref_Vrms]=replaygain('ref_pink.wav',a1,b1,a2,b2);
filename='not empty';
filenumber=0;
filenumber=filenumber+1;
% Ask user for filename to process
filename=input(['enter filename ',num2str(filenumber), ...
' ? '],'s');
% do this loop while ever the user is entering files
% (user hits enter to proceed to calculation)
while length(filename)>0,
% Check if user has entered folder name
if filename(length(filename))=='/' | ...
filename(length(filename))=='\',
% Get directory listing of requested folder
d=dir([filename '*.wav']);
% If the folder exists and contains .wav files in
% the directory
if length(d)>0,
% Store each wavefilename for processing later
for loop=1:length(d)
realfilename=d(loop).name;
filenamematrix(filenumber).name= ...
[filename realfilename (1:length(realfilename)-4)];
end
filename=input(['enter filename ', ...
num2str(filenumber),' ? '],'s');
40
else
% If the folder does nto exist or contains not .wavs,
% ask the user for another name
filename=input(['NOT FOUND. enter filename ', ...
end
% If the user has entered a file name (rather than folder)
else
% Add .wav to end if user failed to include it
if isempty(findstr(filename,'.wav')), filename= ...
[filename '.wav']; end
% Check the file exists
if ~exist(filename,'file'),
filename=input(['NOT FOUND. enter filename ', ...
else
% If it does, store the file name
% Strip .wav from end
filename=filename(1:length(filename)-4);
filenamematrix(filenumber).name=filename;
filename=input(['enter filename ', ...
end
end
end
disp(char(13));
% If no files entered, end the program
if filenumber==1
error('Program Aborted: You must type something!!!');
end
% Start a timer to find out how long this takes!
tic;
% Loop through all the files
for loop=1:filenumber-1,
% Calculate the perceived loudness of the file
% using "replaygain" function.
% Subtract this from reference loudness to give
% actual replay gain relative to 83 dB level
Vrms(loop)=ref_Vrms-replaygain ...
(filenamematrix(loop).name,a1,b1,a2,b2);
% Output the result on screen
ref_Vrms
disp([filenamematrix(loop).name '.wav: ' ...
num2str(Vrms(loop)) ' dB']);
end
disp(char(13));
disp('== ReplayGainScript complete ==');
% Stop timer and display elapsed time
toc
41
function [a1,b1,a2,b2]=equalloudfilt(fs)
% Design a filter to match equal loudness curves
% 9/7/2001
% If the user hasn't specified a sampling frequency, use the CD
% default
if nargin<1,
fs=44100;
end
% Specify the 80 dB Equal Loudness curve
if fs==44100 | fs==48000,
EL80=[0,120;20,113;30,103;40,97;50,93;60,91;70,89;80,87; ...
90,86;100,85;200,78;300,76;400,76;500,76;600,76;700,77; ...
800,78;900,79.5;1000,80;1500,79;2000,77;2500,74;3000,71.5; ...
3700,70;4000,70.5;5000,74;6000,79;7000,84;8000,86;9000,86; ...
10000,85;12000,95;15000,110;20000,125;fs/2,140];
elseif fs==32000,
EL80=[0,120;20,113;30,103;40,97;50,93;60,91;70,89;80,87; ...
90,86;100,85;200,78;300,76;400,76;500,76;600,76;700,77; ...
800,78;900,79.5;1000,80;1500,79;2000,77;2500,74;3000,71.5; ...
3700,70;4000,70.5;5000,74;6000,79;7000,84;8000,86;9000,86; ...
10000,85;12000,95;15000,110;fs/2,115];
else
error('Filter not defined for current sample rate');
end
% convert frequency and amplitude of the equal loudness curve into
% format suitable for yulewalk
f=EL80(:,1)./(fs/2);
m=10.^((70-EL80(:,2))/20);
% Use a MATLAB utility to design a best bit IIR filter
[b1,a1]=yulewalk(10,f,m);
% Add a 2nd order high pass filter at 150Hz to finish the job
[b2,a2]=butter(2,(150/(fs/2)),'high');
42
function Vrms = replaygain(filename,a1,b1,a2,b2)
% Determine the perceived loudness of a file
% METHOD:
% 1) Calculate Vrms every 50ms
% 2) Sort in ascending order of loudness
% 3) Pick the 95% interval (i.e. go 95% up the list,
% and choose the value at this point)
% 4) Convert this value into dB
% 5) return this value.
% Back in the main program...
% 6) Subtract it from that calculated for -20dB FS
% RMS pink noise
% Result = required correction to replay gain
% (relative to 83dB reference)
% David Robinson, 10th July 2001.
% http://www.David.Robinson.org/
% Get information about file
lngth=wavread(filename,'size');
samples=lngth(1);
channels=lngth(2);
% Read sampling rate and No. of bits
[dummy,fs,bs]=wavread(filename,[1 2]);
% The the file isn't CD sample rate, try to
% generate appropriate equal loudness filter
if fs~=44100 || nargin<2,
[a1,b1,a2,b2]=equalloudfilt(fs);
end
%- BELOW, THE BLOCK LENGTH WAS CHANGED
%- IN THE Replay Gain X ms ALGORITHM
%- VERSION //Paul Nygren, 2009-02-24
% Set the Vrms window to 50ms
rms_window_length=round(50*(fs/1000));
%- BELOW, THE PERCENTAGE WAS CHANGED
%- IN THE Replay Gain Y % ALGORITHM
%- VERSION //Paul Nygren, 2009-02-24
% Set the interval to 95%
% Which rms value to take as typical of whole file
percentage=95;
% Set amount of data (in seconds) which
% Matlab on my PC happily copes with at once
% chunk data in from wave file in 2 second blocks
% - file less than this length will cause an error
block_length=2;
% Determine how many rms value to calculate
% per block of data
rms_per_block=fix((fs*block_length)/rms_window_length);
% Check that the file is long enough to
% process in block_length blocks
if lngth<(fs*block_length),
43
warning(['skipping ' filename ' because it is too short']);
Vrms=0;
Vrms_all=0;
return
end
% Display a Waitbar to show user how far into file we are
wbh=waitbar(0,'Processing...');
% Loop through all the file in blocks a defined above
for audio_block=0:fix(samples/(fs*block_length))-1,
% Update the waitbar display to reflect progress
waitbar(audio_block/(fix(samples/(fs*block_length))-1));
% Grab a section of audio
inaudio=wavread(filename,[(fs*block_length*audio_block)+1 ...
fs*block_length*(audio_block+1)]);
% Filter it using the equal loudness curve filter:
inaudio=filter(b1,a1,inaudio);
% Calculate Vrms:
for rms_block=0:rms_per_block-1,
% Mono signal: just do the one channel
if channels==1,
Vrms_all((audio_block*rms_per_block)+rms_block+1)= ...
mean(inaudio((rms_block*rms_window_length)+ ...
1:(rms_block+1)*rms_window_length).^2);
% Stereo signal: take average Vrms of both channels
elseif channels==2,
Vrms_left=mean(inaudio((rms_block*rms_window_length)+ ...
1:(rms_block+1)*rms_window_length,1).^2);
Vrms_right=mean(inaudio((rms_block*rms_window_length) ...
+1:(rms_block+1)*rms_window_length,2).^2);
(Vrms_left+Vrms_right)/2;
end
end
end
% Close the waitbar
close(wbh);
% Convert to dB
Vrms_all=10*log10(Vrms_all+10^-10);
% Sort the Vrms values into numerical order
Vrms_all=sort(Vrms_all);
% Pick the 95% value
Vrms=Vrms_all(round(length(Vrms_all)*percentage/100));
return
44
Appendix E – Matlab code for the ITU-R BS. 1770
implementation
function ITUloudness = ITUOriginal(a1)
%
%--- Loudness calculation according to ITU-R BS. 1770-1 --%
% This script calculates the loudness value
% for a mono or stereo .wav-file according to ITU-R BS. 1770-1
% As input the script requires the name of a .wav-file
% on the form: 'name.wav'. The output is the calculated
% loudness value.
% --- 2009-02-17, Paul Nygren --%
% Reads an audio file
audiofile1=wavread(a1);
%Filter
%of the
Bhead =
Ahead =
coefficients for the modeling
acoustic effects of the head (48kHz)
[1.53512485958697 -2.69169618940638 1.19839281085285];
[1 -1.69065929318241 0.73248077421585];
%RLB filter coefficients (48kHz)
BRLB = [1 -2 1];
ARLB = [1 -1.99004745483398 0.99007225036621];
%filtering and calculation according
%to ITU-R BS. 1770-1 (stereo)
if size(audiofile1,2)==2
af1ch1=filter(Bhead, Ahead, audiofile1(:,1));
af1ch1filt=filter(BRLB, ARLB, af1ch1(:));
af1ch1filtsq=af1ch1filt.^2;
z11=mean(af1ch1filtsq);
loud=-0.691+10*log10(z11+z12);
else
%to ITU-R BS. 1770-1 (mono)
loud=-0.691+10*log10(z11);
end
ITUloudness=loud;
45
Appendix F – Matlab code for the ITU gate
implementation
function ITU = ITUgate(a1)
%
%--- ITU-R BS. 1770 with gate funcion --%
% Calculation according to the ITU standard,
% but values under a given threshold is ignored.
% --- 2009-02-17, Paul Nygren --% Reads an audio file
%Filter
%of the
Bhead =
Ahead =
[1.53512485958697 -2.69169618940638 1.19839281085285];
[1 -1.69065929318241 0.73248077421585];
BRLB = [1 -2 1];
ARLB = [1 -1.99004745483398 0.99007225036621];
%The gate threshold value (this value corresponds to -50dBFS)
%Change to test different threshold values
threshold=0.00001;
%The squared values are sorted
sortedch1=sort(af1ch1filtsq);
%Find the index in the vectors where the
%threshold value is.
a=find(sortedch1<threshold);
b=find(sortedch2<threshold);
%The mean value is calculated including only values over
%the threshold in the vectors sortedch1 and sortedch2
z11=mean(sortedch1((length(a)+1):length(sortedch1)));
z12=mean(sortedch2((length(b)+1):length(sortedch2)));
loud=-0.691+10*log10(z11+z12);
46
else
%to ITU-R BS. 1770-1 (mono)
%threshold value is
%the threshold in the vector sortedch1
loud=-0.691+10*log10(z11);
end
ITU=loud;
47
Appendix G – Matlab code for the ITU strongest
section implementation
function ITUloudness = ITUGate_Strongest(a1)
%
%--- ITU strongest section --%
% This script calculates the loudness value
% for a 2 channel .wav-file according to ITU-R BS. 1770-1
% but only over the strongest section of the file.
% loudness value.
% --- 2009-02-24, Paul Nygren --%
[audiofile1,FS,nbits]=wavread(a1);
%Filter
%of the
Bhead =
Ahead =
[1.53512485958697 -2.69169618940638 1.19839281085285];
[1 -1.69065929318241 0.73248077421585];
BRLB = [1 -2 1];
ARLB = [1 -1.99004745483398 0.99007225036621];
a=0;
afbothchfiltsq=0;
%The channels are summed and
%each sample are indexed and sorted
afbothchfiltsq=af1ch1filtsq+af1ch2filtsq;
temp=afbothchfiltsq';
temp=[temp;(1:length(temp))];
sortedtemp=sortrows(temp');
sortedtemp1=sortedtemp(:,1);
%Values below -50dBFS are ignored
a=find(sortedtemp1<0.000001);
48
b=sortedtemp((length(a)+1):length(sortedtemp),1);
c=sortedtemp((length(a)+1):length(sortedtemp),2);
b=[b c];
b=sortrows(b,2);
%The size of the strongest section is set here
lengthStrongest=round(length(audiofile1)/5);
temp2=sum(b(1:lengthStrongest));
strongest=temp2;
%The strongest section is found
for i=2:(length(b)-(lengthStrongest-1))
temp2=(temp2-b(i-1))+b(lengthStrongest+(i-1));
if temp2>strongest
strongest=temp2;
end
end
strongest=strongest/lengthStrongest;
loud1=-0.691+10*log10(strongest);
else
disp('--- Error: not a stereo audio file ---')
end
ITUloudness=loud1;
49
Appendix H – Matlab code for the ITU with
Replay Gain filter implementation
function ITURGloudness = ITUwithRG(a1)
%
%--- ITU with Replay Gain filter --%
% This script calculates loudness value for a mono or
% stereo .wav-file according to the ITU standard but using
% the weighting filters from Replay Gain.
%
% loudness value.
% --- 2009-02-24, Paul Nygren --[audiofile1, fs, NBITS]=wavread(a1);
%Getting the filter coefficients for the
%Replay Gain filters
[A1,B1,A2,B2]=equalloudfilt(fs);
%Stereo file calculation process according to
%the ITU standard but with the Replay Gain
%filter coefficients instead
af1ch1=filter(B1,A1, audiofile1(:,1));
af1ch1filt=filter(B2, A2, af1ch1(:));
loud1=-0.691+10*log10(z11+z12);
%Mono file calculation process according to
%the ITU standard but with the Replay Gain
%filter coefficients instead
else
loud1=-0.691+10*log10(z11);
end
ITURGloudness=loud1;
50
The code below is from the website www.replaygain.org (Replay Gain 2008)
function [a1,b1,a2,b2]=equalloudfilt(fs)
% Design a filter to match equal loudness curves
% 9/7/2001
% If the user hasn't specified a sampling frequency, use the CD
% default
if nargin<1,
fs=44100;
end
% Specify the 80 dB Equal Loudness curve
if fs==44100 | fs==48000,
EL80=[0,120;20,113;30,103;40,97;50,93;60,91;70,89;80,87; ...
90,86;100,85;200,78;300,76;400,76;500,76;600,76;700,77; ...
800,78;900,79.5;1000,80;1500,79;2000,77;2500,74;3000,71.5; ...
3700,70;4000,70.5;5000,74;6000,79;7000,84;8000,86;9000,86; ...
10000,85;12000,95;15000,110;20000,125;fs/2,140];
elseif fs==32000,
EL80=[0,120;20,113;30,103;40,97;50,93;60,91;70,89;80,87; ...
90,86;100,85;200,78;300,76;400,76;500,76;600,76;700,77; ...
800,78;900,79.5;1000,80;1500,79;2000,77;2500,74;3000,71.5; ...
3700,70;4000,70.5;5000,74;6000,79;7000,84;8000,86;9000,86; ...
10000,85;12000,95;15000,110;fs/2,115];
else
error('Filter not defined for current sample rate');
end
% convert frequency and amplitude of the equal loudness curve into
% format suitable for yulewalk
f=EL80(:,1)./(fs/2);
m=10.^((70-EL80(:,2))/20);
% Use a MATLAB utility to design a best bit IIR filter
[b1,a1]=yulewalk(10,f,m);
% Add a 2nd order high pass filter at 150Hz to finish the job
[b2,a2]=butter(2,(150/(fs/2)),'high');
51
Appendix I – Matlab code for the Replay Gain
with ITU filter implementation
(The Replay Gain algorithm function that differs from the original implementation is
shown below. For the other two functions see Appendix D.)
function Vrms = replaygainITU(filename,a1,b1,a2,b2)
% Determine the perceived loudness of a file
% METHOD:
% 1) Calculate Vrms every 50ms
% 2) Sort in ascending order of loudness
% 3) Pick the 95% interval (i.e. go 95% up the list,
% and choose the value at this point)
% 4) Convert this value into dB
% 5) return this value.
% Back in the main program...
% 6) Subtract it from that calculated for -20dB FS
% RMS pink noise
% Result = required correction to replay gain
% (relative to 83dB reference)
% David Robinson, 10th July 2001.
% http://www.David.Robinson.org/
% Get information about file
lngth=wavread(filename,'size');
samples=lngth(1);
channels=lngth(2);
% Read sampling rate and No. of bits
[dummy,fs,bs]=wavread(filename,[1 2]);
%- FILTER COEFFICIENTS FOR THE MODELING
%- OF THE ACOUSTIC EFFECTS OF THE HEAD (48kHz)
%- //Paul Nygren, 2009-02-24
Bhead = [1.53512485958697 -2.69169618940638 1.19839281085285];
Ahead = [1 -1.69065929318241 0.73248077421585];
%- THE RLB WEIGHTING FILTER COEFFICIENTS
%- //Paul Nygren, 2009-02-24
BRLB = [1 -2 1];
ARLB = [1 -1.99004745483398 0.99007225036621];
% Set the Vrms window to 50ms
rms_window_length=round(50*(fs/1000));
% Set the interval to 95%
% Which rms value to take as typical of whole file
percentage=95;
% Set amount of data (in seconds) which
% Matlab on my PC happily copes with at once
% chunk data in from wave file in 2 second blocks
% - file less than this length will cause an error
block_length=2;
% Determine how many rms value to calculate
52
% per block of data
rms_per_block=fix((fs*block_length)/rms_window_length);
% Check that the file is long enough to
% process in block_length blocks
if lngth<(fs*block_length),
warning(['skipping ' filename ' because it is too short']);
Vrms=0;
Vrms_all=0;
return
end
% Display a Waitbar to show user how far into file we are
wbh=waitbar(0,'Processing...');
% Loop through all the file in blocks a defined above
for audio_block=0:fix(samples/(fs*block_length))-1,
% Update the waitbar display to reflect progress
waitbar(audio_block/(fix(samples/(fs*block_length))-1));
% Grab a section of audio
inaudio=wavread(filename,[(fs*block_length*audio_block)+1 ...
fs*block_length*(audio_block+1)]);
% Filter it using the equal loudness curve filter:
% Calculate Vrms:
for rms_block=0:rms_per_block-1,
% Mono signal: just do the one channel
if channels==1,
mean(inaudio((rms_block*rms_window_length)+ ...
1:(rms_block+1)*rms_window_length).^2);
% Stereo signal: take average Vrms of both channels
elseif channels==2,
Vrms_left=mean(inaudio((rms_block*rms_window_length)+ ...
1:(rms_block+1)*rms_window_length,1).^2);
Vrms_right=mean(inaudio((rms_block*rms_window_length) ...
+1:(rms_block+1)*rms_window_length,2).^2);
(Vrms_left+Vrms_right)/2;
end
end
end
% Close the waitbar
close(wbh);
% Convert to dB
Vrms_all=10*log10(Vrms_all+10^-10);
% Sort the Vrms values into numerical order
Vrms_all=sort(Vrms_all);
% Pick the 95% value
Vrms=Vrms_all(round(length(Vrms_all)*percentage/100));
return
53
Appendix J – Matlab code for the RLB
implementation
function RLBloudness = RLB (a1)
%
%--- RLB loudness calculation --%
% This script calculates the RLB loudness value
% for a mono or stereo .wav-file.
% loudness value.
% --- 2009-02-24, Paul Nygren --%
BRLB = [1 -2 1];
ARLB = [1 -1.99004745483398 0.99007225036621];
%to RLB (stereo)
af1ch1filt=filter(BRLB, ARLB, audiofile1(:,1));
loud=-0.691+10*log10(z11+z12);
else
%to RLB (mono)
loud=-0.691+10*log10(z11);
end
RLBloudness=loud;
54
Appendix K – Matlab code for the RLB gate
implementation
function RLBgate = RLBgate(a1)
%
%--- RLB loudness calculation with gate funcion --%
% Calculation according to RLB,
% but values under a given threshold is ignored.
% --- 2009-02-24, Paul Nygren --% Reads an audio file
BRLB = [1 -2 1];
ARLB = [1 -1.99004745483398 0.99007225036621];
%The gate threshold value (this value corresponds to -50dBFS)
%Change to test different threshold values
threshold=0.00001;
%to RLB (stereo)
%threshold value is.
b=find(sortedch2<threshold);
%the threshold in the vectors sortedch1 and sortedch2
z12=mean(sortedch2((length(b)+1):length(sortedch2)));
loud=-0.691+10*log10(z11+z12);
55
else
%to RLB (mono)
%threshold value is
%the threshold in the vector sortedch1
loud=-0.691+10*log10(z11);
end
RLBgate=loud;
56
Appendix L – Matlab code for the regression
analysis
Matlab code for the regression analysis, including the DifferenceLevel values from the
listening experiment.
%y1 to y16 represent the 16 test subjects and their 36
%DifferenceLevel values (the experiment normalization
%process is accounted for)
y1=[16.31; -0.49; -11.49; -0.27; -5.40; -0.74
NaN %Test subject mistake during experiment
1.97; 13.35; 9.71; 2.66; 2.66; -21.05; -7.03
12.45; 12.37; -7.27; 5.60; 5.26; 0.51; 2.96
5.61; -6.20; 4.20; 10.93; -12.92; -2.04; 10.22
6.40; -8.39; -0.69; 5.08; -12.92; 9.01; 1.20
-11.61];
%Test subject 1
y2=[13.21; -0.89; -13.99; -1.47; -1.10; -3.74
-1.02; 0.72; 16.95; 11.31; -1.29; 2.96; -21.10
-8.33; 14.65; 12.57; -12.07; 6.05; 5.86; 1.41
4.36; 8.96; -5.75; 4.30; 15.28; -15.32; -2.19
10.07; 9.90; -12.33; 0.06; 7.18; -13.72; 15.81
0.86; -8.16]; %Test subject 2
y3=[13.16; -1.49; -10.29; -5.42; -2.55; -1.99
1.18; 0.62; 14.80; 9.41; 0.41; 2.46; -18.10
-10.18; 11.45; 12.02; -6.18; 4.90; 3.41; 0.21
5.01; 8.01; -7.15; 3.15; 10.08; -8.77; -1.49
10.17; 9.15; -11.08; -0.59; 5.93; -12.47; 9.51
-3.55; -10.36]; %Test subject 3
y4=[15.86; 0.66; -12.29; -3.37; -4.35; -3.19
0.48; -1.23; 14.80; 10.81; -0.14; 5.06; -18.10
-5.33; 11.90; 11.02; -7.52; 5.35; 3.96; 1.66
2.51; 7.61; -6.85; 1.50; 14.28; -12.27; -1.54
9.57; 4.50; -12.24; 1.06; 6.13; -15.97; 11.56
-0.65; -11.51]; %Test subject 4
y5=[16.01; 1.41; -9.64; -2.37; -1.95; -4.64
2.68; 0.17; 11.85; 8.86; 3.21; 7.76; -17.95
-7.48; 13.50; 11.07; -8.52; 4.11; 3.16; -0.49
1.16; 5.06; -5.60; 2.85; 11.53; -11.57; -2.09
10.47; 12.70; -11.19; 0.36; 5.28; -14.32; 13.31
-0.69; -12.36]; %Test subject 5
y6=[17.41; -2.39; -19.79; -7.47; -0.45; 3.41
0.28; -0.23; 16.15; 11.36; 1.36; 1.46; -18.80
-8.78; 12.30; 12.97; -14.17; 4.36; 3.16; 4.16
8.06; 11.91; -9.00; 2.90; 14.53; -14.32; 0.71
11.27; 9.10; -11.44; 0.81; 8.93; -15.42; 10.36
1.86; -7.81]; %Test subject 6
y7=[14.61; 0.36; -11.49; -2.97; -3.40; -0.69
1.43; 0.47; 15.90; 10.26; 0.36; 4.96; -18.05
57
-6.38; 11.75; 11.82; -8.83; 7.31; 5.41; 0.06
3.76; 5.51; -7.50; 4.25; 11.83; -10.92; -0.89
10.27; 8.55; -11.48; 0.06; 4.83; -13.57; 12.16
-0.15; -12.21]; %Test subject 7
y8=[12.46; 2.16; -14.79; -0.07; -2.45; 0.01
3.23; 2.07; 13.70; 5.31; 1.41; 2.91; -21.60
-7.78; 13.10; 7.82; -7.77; 5.01; 3.41; -1.24
2.46; 5.86; -6.60; 4.15; 10.63; -7.37; -0.54
8.12; 6.40; -9.69; 1.01; 3.68; -12.42; 9.86
-1.09; -7.86]; %Test subject 8
y9=[12.16; -0.54; -6.99; 0.08; -7.75; -2.79
2.88; 2.97; 10.25; 8.41; 3.36; 7.16; -16.15
-6.08; 10.55; 11.37; -4.83; 6.35; 2.56; -2.99
1.51; 8.36; -5.65; 3.65; 9.63; -9.32; -2.74
6.27; 7.95; -8.88; -3.64; 4.78; -11.57; 12.71
-2.75; -10.66]; %Test subject 9
y10=[11.91; 1.31; -9.49; -4.97; -4.60; -1.19
2.53; 1.62; 10.15; 6.51; 2.41; 3.96; -17.30
-6.28; 8.85; 11.32; -6.73; 9.06; 5.76; -0.29
1.01; 5.96; -7.75; 2.80; 8.48; -9.47; -1.49
8.97; 6.10; -9.59; -0.89; 2.28; -12.07; 9.86
-0.55; -11.71]; %Test subject 10
y11=[12.56; 0.61; -12.44; -5.12; -3.55; -1.59
0.63; -0.68; 9.35; 7.96; 1.86; 2.21; -18.20
-8.58; 9.25; 11.42; -5.78; 4.91; 4.11; -3.09
2.01; 4.86; -7.65; 3.15; 9.28; -9.82; -1.54
9.42; 7.95; -9.44; -0.54; 4.93; -14.17; 9.71
1.26; -11.26]; %Test subject 11
y12=[13.71; 0.91; -2.84; 1.83; -4.25; -0.39
1.83; 3.47; 12.40; 8.51; 5.61; 6.76; -13.65
-7.13; 12.00; 9.17; -2.93; 7.56; 2.41; -1.24
3.26; 6.86; -7.00; 2.95; 9.38; -9.17; 0.86
9.22; 9.15; -2.09; -0.84; 3.58; -9.97; 14.06
-2.39; -10.21]; %Test subject 12
y13=[16.06; 1.71; -16.79; -1.37; -0.15; -1.34
0.43; 1.67; 15.40; 9.71; -0.34; 2.21; -22.75
-11.83; 15.65; 13.07; -10.73; 4.66; 2.86; -0.54
2.56; 8.11; -5.35; 4.15; 14.83; -14.87; -0.74
9.72; 7.15; -11.09; 0.56; 8.63; -13.67; 12.51
-1.65; -9.21]; %Test subject 13
y14=[10.51; -1.54; -12.59; -1.12; -1.40; -1.09
0.73; 1.77; 14.40; 9.21; 3.81; 4.21; -18.75
-8.18; 8.85; 8.02; -7.12; 7.91; 3.91; -1.74
2.31; 8.61; -6.45; 3.45; 10.43; -7.72; -0.49
9.57; 5.90; -11.19; 1.31; 5.83; -12.42; 12.11
-1.45; -11.96]; %Test subject 14
58
y15=[15.06; 1.46; -6.44; 0.58; -2.50; -3.49
-0.27; 0.82; 11.05; 11.21; 3.41; 5.41; -17.05
-2.58; 10.65; 11.22; -8.47; 8.05; 6.26; 2.41
3.56; 5.66; -6.80; 1.80; 11.83; -9.42; -1.29
10.12; 4.90; -5.98; -1.69; 4.48; -10.42; 10.01
1.81; -12.21]; %Test subject 15
y16=[13.96; 0.91; -10.69; 0.83; -4.05; -3.79
0.03; 0.92; 12.35; 9.76; 0.46; 6.76; -19.45
-7.78; 11.65; 11.02; -9.22; 6.05; 6.16; -0.34
2.76; 5.11; -6.45; 3.00; 9.73; -11.92; -0.34
12.82; 7.90; -9.64; -0.44; 6.33; -12.77; 9.86
-0.09; -11.66]; %Test subject 16
%The DifferenceLevel values of the 16 test subjects in one row
%vector.
y=[y1;y2;y3;y4;y5;y6;y7;y8;
y9;y10;y11;y12;y13;y14;y15;y16];
%A matrix representing which audio files that were matched during
%a listening experiment session
x=zeros(36,24);
x(1,1)=1;
x(1,2)=-1;
x(2,1)=1;
x(2,13)=-1;
x(3,2)=1;
x(3,3)=-1;
x(4,2)=1;
x(4,14)=-1;
x(5,3)=1;
x(5,4)=-1;
x(6,3)=1;
x(6,15)=-1;
x(7,4)=1;
x(7,5)=-1;
x(8,4)=1;
x(8,16)=-1;
x(9,5)=1;
x(9,6)=-1;
x(10,5)=1;
x(10,17)=-1;
x(11,6)=1;
x(11,7)=-1;
x(12,6)=1;
x(12,18)=-1;
x(13,7)=1;
x(13,8)=-1;
x(14,7)=1;
x(14,19)=-1;
x(15,8)=1;
x(15,9)=-1;
x(16,8)=1;
x(16,20)=-1;
x(17,9)=1;
x(17,10)=-1;
x(18,9)=1;
x(18,21)=-1;
59
x(19,10)=1;
x(19,11)=-1;
x(20,10)=1;
x(20,22)=-1;
x(21,11)=1;
x(21,12)=-1;
x(22,11)=1;
x(22,23)=-1;
x(23,12)=1;
x(23,13)=-1;
x(24,12)=1;
x(24,24)=-1;
x(25,13)=1;
x(25,14)=-1;
x(26,14)=1;
x(26,15)=-1;
x(27,15)=1;
x(27,16)=-1;
x(28,16)=1;
x(28,17)=-1;
x(29,17)=1;
x(29,18)=-1;
x(30,18)=1;
x(30,19)=-1;
x(31,19)=1;
x(31,20)=-1;
x(32,20)=1;
x(32,21)=-1;
x(33,21)=1;
x(33,22)=-1;
x(34,22)=1;
x(34,23)=-1;
x(35,23)=1;
x(35,24)=-1;
x(36,24)=1;
x(36,1)=-1;
%Matlab needed a constant term, see Matlab help for information
%about “regress”
x=[ones(36,1) x];
%One x matrix for each test subject
X=[x;x;x;x;x;x;x;x;x;x;x;x;x;x;x;x];
%B corresponds to the SegmentLevel values which is the
%result from the regression analysis
B = regress(y,X)
60
TRITA-CSC-E 2009:032
ISRN-KTH/CSC/E--09/032--SE
ISSN-1653-5715
www.kth.se

Achieving Equal Loudness between Audio Files

Transcription

Similar documents

Bticino 334202 (5 Wire)

Step # 13 Open up TMPGEnc 4.0 Express and click on “Start a new

Q-Bass-U 2.1 Audio - LTB Audio Systems

A Visual History of Loudness

24 News

Read the show blog

Summer-Newsletter2014

SB-GM-C7CP1/10TW3

Contents - February 2002

SB-LR-4/10TW3