KULTUSMINISTERIUM DES LANDES SACHSEN

Transcription

SCHRIFTLICHE ABITURPRÜFUNG 2003
MATHEMATIK (GRUNDKURS)
KULTUSMINISTERIUM DES LANDES SACHSEN-ANHALT
Abitur
April/Mai 2003
Mathematik
(Grundkurs)
Arbeitszeit: 210 Minuten
Der Prüfling wählt je eine Aufgabe aus den Gebieten G 1, G 2 und G 3 zur Bearbeitung aus.
Gewählte Aufgaben (Die drei zur Bewertung vorgesehenen Aufgaben sind vom Prüfling anzukreuzen.):
Gebiet G 1
Gebiet G 2
Gebiet G 3
Aufgabe 1.1
Aufgabe 2.1
Aufgabe 3.1
Aufgabe 1.2
Aufgabe 2.2
Aufgabe 3.2
Unterschrift Prüfling:
Gebiet G 1
Aufgabe 1.1
Analysis
Ein Unternehmen stellt u. a. Monitore für PCs her. Bei der Herstellung von x Monitoren entstehen Kosten K(x). Die Kosten (in €) in Abhängigkeit von x werden durch die Gleichung
K(x) = 0,001x³ – 1,29x² + 600x + 12000
beschrieben.
Der Verkauf der Monitore an die Händler erfolgt zum Preis von 300 € pro Stück. Die Einnahmen beim Verkauf von x Monitoren werden mit E(x) und der Gewinn, den das Unternehmen dabei erzielt, mit G(x) bezeichnet (jeweils in €). Der Gewinn ist dabei die Differenz aus
den Einnahmen und den Kosten.
a) Untersuchen Sie die Funktion K mit K(x) und x ∈ R , x ≥ 0 auf Existenz von lokalen Extremstellen, auf Monotonie sowie auf ihr Verhalten für x → ∞ .
Berechnen Sie die Koordinaten des Wendepunktes.
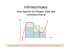
Die Abbildung zeigt den Graphen der Funktion K im Intervall 0 ≤ x ≤ 1000.
Interpretieren Sie ihn unter
dem Aspekt der Kostenentwicklung.
K(x)
x
b) Stellen Sie jeweils eine Gleichung für die Funktionen E mit E(x) und G mit G(x) und x ∈ R,
x ≥ 0 auf.
Begründen Sie, dass x1 = 357,8 und x2 = 966,9 Näherungswerte für die Nullstellen der
Funktion G sind.
Ermitteln Sie die Koordinaten und die Art der lokalen Extrempunkte des Graphen von G.
Zeichnen Sie die Graphen von G und E im Intervall 0 ≤ x ≤ 1000.
Interpretieren Sie den Graphen von G hinsichtlich Gewinn und Verlust und geben Sie den
maximalen Gewinn an.
c) Für die Funktion G gilt im Intervall der Nullstellen [x1; x2] (siehe Aufgabe b):
x2
∫ G( x )dx = ( x 2 − x 1 ) ⋅ G( x )
x1
mit x ∈ [x 1; x 2 ] .
Deuten Sie die Stelle x im Zusammenhang mit dem Gewinn.
Geben Sie eine Stammfunktion der Funktion G an.
Gebiet G 1
Gegeben ist die Funktion f durch y = f ( x ) = x +
Aufgabe 1.2
Analysis
1
+2
x
mit x ∈ R und x ≠ 0.
Der zugehörige Graph wird mit F bezeichnet.
a) Ermitteln Sie die Nullstelle und die Polstelle der Funktion f.
Ermitteln Sie die Lage und die Art der lokalen Extrempunkte des Graphen F und weisen
Sie nach, dass der Graph F keine Wendepunkte hat.
Zeigen Sie, dass die Gerade mit der Gleichung y = x + 2 eine Asymptote des Graphen F
ist.
Zeichnen Sie den Graphen F im Intervall –7 ≤ x ≤ 7.
Geben Sie die Monotonieintervalle der Funktion f an.
b) Geben Sie den Wertebereich der Funktion f an.
Zeigen Sie, dass aus dem Wertebereich der Funktion f die Gültigkeit der Ungleichung
1
x + ≥ 2 für alle x mit x ≠ 0 gefolgert werden kann.
x
c) Ermitteln Sie zwei voneinander verschiedene Stammfunktionen der Funktion f und geben
Sie an, wodurch sich die Graphen dieser beiden Stammfunktionen unterscheiden.
Der Graph F und die Gerade mit der Gleichung y = –4 schließen eine Fläche vollständig
ein. Berechnen Sie die Maßzahl des Inhalts dieser Fläche.
Gebiet G 2
Aufgabe 2.1
Analytische Geometrie
In einem kartesischen Koordinatensystem sind die Kreise
k1:
k2:
(x + 5)2 + (y – 7)2 = 5 ,
(x – 4)2 + (y – 10)2 = 20
gegeben.
a) Ermitteln Sie eine Gleichung der Tangente t an den Kreis k1 im Punkt B1(–3 | 6).
[Ergebnis zur Kontrolle: y = 2x +12]
Zeigen Sie, dass die Tangente t auch Tangente des Kreises k2 ist und berechnen Sie die
Koordinaten des Berührungspunktes B2.
b) Ermitteln Sie von der Geraden g, die durch die Mittelpunkte der Kreise k1 und k2 geht,
eine Parametergleichung und eine Gleichung in der Form y = mx + n.
Berechnen Sie die Koordinaten des Schnittpunktes und das Gradmaß des Schnittwinkels
der Geraden g und t (siehe Aufgabe a).
c) Die Abbildung zeigt verschiedene Fälle von Lagebeziehungen zweier Kreise mit gemeinsamer Tangente.
Untersuchen Sie, welcher dieser Fälle für die gegebenen Kreise k1 und k2 zutrifft.
Die Lage des Kreises k2 soll (bei gleichbleibendem Radius) so verändert werden, dass
einer der übrigen Fälle der in der Abbildung gegebenen Lagebeziehungen zutrifft.
Wählen Sie dafür eine Lagebeziehung aus und ermitteln Sie die Koordinaten des Mittelpunktes des Kreises k2 für diesen Fall.
Abbildung (nicht maßstäblich)
Gebiet G 2
Aufgabe 2.2
Ein Flugzeug fliegt auf geradlinigem Kurs vom Punkt A(–50 | 31 | 4) in Richtung des
Punktes B(–14 | 7 | 1). Die Beschreibung des geometrischen Sachverhaltes erfolgt in einem
kartesischen Koordinatensystem; eine Einheit entspricht einem Kilometer. Die x-y-Ebene
charakterisiert die Horizontalebene.
a) Ermitteln Sie einen Vektor, der die Flugrichtung beschreibt und berechnen Sie die Länge
der Flugstrecke zwischen den Punkten A und B.
Der Flug muss aus Sicherheitsgründen oberhalb einer Ebene E mit der Gleichung
x – y + 20 z + 11 = 0 stattfinden.
Zeigen Sie, dass das Flugzeug oberhalb der Ebene E und in einem konstanten Abstand
zu dieser Ebene fliegt.
 18 


Vom Punkt B aus erfolgt ein geradliniger Landeanflug in Richtung des Vektors a =  − 9  .
 − 1


→
b) Berechnen Sie das Gradmaß des Winkels, der die Kursänderung im Punkt B für den
Landeanflug angibt.
Berechnen Sie das Gradmaß des Winkels, unter dem der Landeanflug zur Horizontalebene erfolgt.
Geben Sie eine Gleichung der Geraden g an, die den Landeanflug charakterisiert und
berechnen Sie die Koordinaten des Punktes L der Horizontalebene, in dem das Flugzeug
aufsetzt.
Die Landebahn des Flughafens werde als Strecke betrachtet, deren Punkte wie folgt
 15 


4 
 2

→
 
15 

beschrieben sind:
t ∈ R, 0 ≤ t ≤ 1.
x =  −  + t  − 1 ,
8




 0
 0 


c) Zeigen Sie, dass das Flugzeug im ersten Viertel der Landebahn aufsetzt.
Gebiet G 3
Aufgabe 3.1
Stochastik
Eine TÜV-Station hat die häufigsten Mängel an fünf Jahre alten Pkws erfasst. Es wurden
2000 Pkws untersucht.
Mängel
A:
B:
C:
D:
E:
F:
G:
S:
Handbremse (mit zu geringer Bremswirkung)
Ölverlust (an Motor oder Getriebe)
Auspuffanlage (korrodiert)
Scheinwerfereinstellung (Blendwirkung)
Bereifung (schadhaft oder mit zu geringer Profiltiefe)
Katalysator (Lambdasonde defekt)
Rost (mit Auswirkung auf die Fahrsicherheit)
Sonstige
relative Häufigkeit in %
7,8
7,5
5,0
4,3
3,9
2,5
0,5
18,7
Es wird davon ausgegangen, dass die Mängel A bis S unabhängig voneinander auftreten.
a) Begründen Sie, dass die angegebenen relativen Häufigkeiten als Wahrscheinlichkeiten
für das Auftreten der Mängel A bis S angesehen werden dürfen.
Ermitteln Sie die Wahrscheinlichkeiten der folgenden Ereignisse für fünf Jahre alte Pkws:
E1:
Ein Pkw hat den Mangel B.
E2:
Ein Pkw hat die Mängel A und B.
E3:
Ein Pkw hat den Mangel A oder den Mangel B.
b) Ermitteln Sie die Wahrscheinlichkeit dafür, dass höchstens 6 von 100 Pkws einen Mangel
an der Auspuffanlage (Mangel C) aufweisen.
Die TÜV-Station vermutet aufgrund neuer Prüfberichte, dass nur noch höchstens 5 % aller
fünf Jahre alten Pkws den Mangel B aufweisen.
Die Zufallsgröße X beschreibe die Anzahl der Pkws mit dem Mangel B in einer Stichprobe
vom Umfang n = 100. Die Zufallsgröße X wird als binomialverteilt angenommen: X ∼ B100; 0,05.
c) Berechnen Sie den Erwartungswert der Zufallsgröße X.
Prüfen Sie die Nullhypothese H0: p0 ≤ 0,05 auf dem Signifikanzniveau α = 0,05, indem
Sie den Wert k aus P(X ≥ k) = 1 – B100; 0,05({0; 1; ...; k – 1}) ≤ 0,05 ermitteln und den Ablehnungsbereich A für die Nullhypothese H0 angeben.
In der Stichprobe sind sechs Pkws mit dem Mangel B gezählt worden. Wie muss die
TÜV-Station hinsichtlich der Nullhypothese H0 entscheiden?
Gebiet G 3
Aufgabe 3.2
Stochastik
Ein Hobbygärtner züchtet Blumen, deren Samen er selbst gewinnt. Für ein Blumenbeet werden 50 Samenkörner einer Blumensorte ausgesät.
a) Der Hobbygärtner nimmt an, dass die Wahrscheinlichkeit für die Keimfähigkeit 80 %
beträgt. Betrachtet wird die Zufallsgröße X: „Anzahl der keimenden Samenkörner“. Diese
wird als binomialverteilt angenommen.
Beschreiben Sie verbal das Ereignis, das durch die Ungleichungen 29 < X ≤ 45 dargestellt wird.
Berechnen Sie die Wahrscheinlichkeit, dass
- mehr als 40 Samenkörner keimen;
- höchstens fünf Samenkörner nicht keimen.
b) Berechnen Sie, welche Wahrscheinlichkeit für die Keimfähigkeit mindestens anzunehmen ist, wenn mit mindestens 50 % Wahrscheinlichkeit alle 50 ausgesäten Samenkörner
keimen.
Für eine Gartenbauausstellung soll ein großes Beet mit 1250 Pflanzen bepflanzt werden. Der
Lieferant der Pflanzen sichert zu, dass eine Pflanze mit 90 % Wahrscheinlichkeit bis zur
Eröffnung blüht.
c) Berechnen Sie die Wahrscheinlichkeit, mit der mehr als 1125 Blumen zur Eröffnung
blühen, in dem Sie die Verteilung der Zufallsgröße Y (mit Y: „Anzahl der blühenden
Pflanzen“) mit der Normalverteilung approximieren.
HINWEISE ZUR KORREKTUR UND BEWERTUNG
Gebiet G 1
Aufgabe
a)
Aufgabe 1.1
Analysis
BE Hinweise, Lösungen
6
Untersuchen von K auf die Existenz von lokalen Extremstellen, auf das Verhalten für
x→ ∞ und auf Monotonie, z. B.:
K′( x ) = 0,003x 2 − 2,58x + 600
K ′ ≠ 0 für alle x ∈ R ⇒ keine lokalen Extremstellen
lim K( x ) = ∞
x →∞
K ′( x ) = 0,003 [( x − 430)² + 15100] > 0 für alle x, d. h. K streng monoton wachsend
b)
4
Berechnen der Koordinaten des Wendepunktes, z. B.:
K ′′( x ) = 0,006 x − 2,58 = 0 ; K ′′′( x ) = 0,006 ≠ 0 Æ xw = 430; yw = 110 986
2
Interpretation des Graphen von K, z. B.:
K beschreibt die Kostenentwicklung: Anfänglich starker Kostenanstieg, dann geringerer Kostenanstieg (bis zum Wendepunkt), danach wieder starker Kostenanstieg.
2
Aufstellen der Gleichungen, z. B.:
E( x ) = 300x , G( x ) = −0,001x 3 + 1,29 x 2 − 300x − 12000
Begründen, dass x1 und x2 Näherungswerte für die Nullstellen von G sind, z. B.:
Wegen Stetigkeit und G(357,7) = –22,9 < 0 und G(357,9) = 24,9 > 0 bzw. G(966,8)
= 55,8 > 0 und G(966,9) = –5,2 < 0
Ermitteln der Koordinaten und der Art der lokalen Extrempunkte des Graphen von G,
z. B.:
G ′( x ) = −0,003 x 2 + 2,58 x − 300 , G′( x ) = 0 , x1 ≈ 138,6 x2 ≈ 721,4
G′′( x ) = −0,006 x + 2,58 , G′′(138,6) ≈ 1,7 > 0 , G′′(721,4) ≈ −1,7 < 0
T(138,6 | –31461,7)
H(721,4 | 67489,7)
4
6
4
Zeichnen der Graphen
von E und G, z. B.:
E
G
x
c)
3
Interpretieren des Graphen G und Angabe des maximalen Gewinns, z. B.:
Gewinn für x1 < x < x2 ; Verlust für 0 ≤ x < x1 bzw. x > x2
Gewinn ist für x = 721 maximal; maximaler Gewinn: ≈ 67 490 €
2
Deuten der Stelle x , z. B.:
x gibt die Stelle im Intervall [x1; x2] an, an der der Gewinn den Durchschnittswert
annimmt.
2
Angeben einer Stammfunktion von G, z. B.:
Γ(x) = − 0,00025 x 4 + 0,43 x 3 − 150 x 2 − 12000 x
35
Gebiet G 1
Aufgabe
a)
Aufgabe 1.2
Analysis
BE
Hinweise, Lösungen
4
Ermitteln der Nullstelle und der Polstelle von f, z. B.:
xN = –1; xP = 0
7
Ermitteln der Lage und der Art der lokalen Extrempunkte des Graphen F und Nachweisen, dass F keine Wendepunkte hat, z. B.:
hinreichende Bedingung erfüllt für Hochpunkt H(–1 | 0) und Tiefpunkt
T(1 | 4), wobei f ′′( −1) = −2 und f ′′(1) = 2
keine Wendepunkte, da notwendige Bedingung nicht erfüllt
2
Zeigen, dass die Gerade mit der Gleichung y = x + 2 eine Asymptote ist, z. B.:
lim ( f ( x ) − ( x + 2)) = 0
y
x →±∞
4
Zeichnen des Graphen F
x
4
Angeben der Monotonieintervalle, z. B.:
monoton wachsend: –∞ < x ≤ –1; 1 ≤ x < ∞;
monoton fallend: –1 ≤ x < 0; 0 < x ≤ 1
b)
4
Angeben des Wertebereiches und Gültigkeit der Ungleichung zeigen, z. B.:
WB: f(x) ≤ 0 oder f(x) ≥ 4
1
1
Für x < 0 gilt also x + + 2 ≤ 0 und für x > 0 gilt x + + 2 ≥ 4 .
x
x
1
Daraus folgt: x + ≥ 2 für alle x mit x ≠ 0.
x
c)
4
Ermitteln von zwei Stammfunktionen und Angeben von Unterschieden der zugehörigen Graphen, z. B.:
Φ 1( x) =
x2
2
+ ln x + 2x und Φ 2 ( x ) =
x2
2
+ ln x + 2x + 3
Die Graphen der Stammfunktionen gehen durch Verschiebung in y-Richtung auseinander hervor.
6
Berechnen der Maßzahl des Inhalts der Fläche, z. B.:
Integrationsgrenzen: x 1;2 = −3 ± 2 2 ; x1 ≈ –5,83; x2 ≈ –0,17
x2
A = ∫ ( f ( x ) + 4)dx ≈ 13,4
x1
35
Gebiet G 2
Aufgabe
a)
b)
Aufgabe 2.1
BE
Hinweise, Lösungen
3
Ermitteln einer Gleichung der Tangente, z. B.:
(x +5)(–3 + 5) + (y – 7)(6 – 7) = 5
⇒ y = 2x + 12
3
Zeigen, dass t auch Tangente vom Kreis k2, z. B.:
I
(x – 4)2 + (y – 10)2 = 20
II
y = 2 x + 12
⇒ genau eine Lösung
⇒ t ist Tangente im Punkt B2 (0 | 12)
4
Ermitteln von Gleichungen der Geraden g, z. B.:
→
 − 5
3
g:
x =   + t  
 7
 1
y=
c)
1
26
x+
3
3
4
Berechnen der Koordinaten des Schnittpunktes und des Gradmaßes des Schnittwinkels, z. B.:
1
26
I
y= x+
3
3
II
y = 2 x + 12
⇒
S(–2 | 8)
1
2−
3
tan α =
⇒
α = 45°
1
1+ 2 ⋅
3
2
Untersuchen, welche Lage der Kreise vorliegt, z. B.:
Untersuchen mittels Zeichnen oder analytischer Betrachtung
→
→
→
→
 − 2
 4
, B 2 M 2 = 
 ⇒
(1) B 1M1 = 
B 1M1 ↑↓ B 2 M 2
 1
 − 2
(2) B1 ≠ B2
Aus (1) und (2) folgt Fall 5 der dargestellten Lagebeziehungen.
4
Auswählen einer Lagebeziehung und Ermitteln der Koordinaten des Mittelpunktes,
z. B.:
Fall 4
→
→
→
OM '2 = OB 1 + B 2 M 2 ⇒
20
M'2(1 | 4)
Gebiet G 2
Aufgabe
a)
Aufgabe 2.2
BE
Hinweise, Lösungen
3
Ermitteln eines Vektors und Berechnen der Länge der Flugstrecke, z. B.:
 12 


→
v =  − 8
 − 1


Flugstrecke: 43,4 km
4
Zeigen, dass Flug oberhalb der Ebene E und mit gleichem Abstand zu dieser Ebene
erfolgt, z. B.:
Für A(–50 | 31 | 4) gilt z > 1 (–x + y – 11) ⇒ A liegt oberhalb von E
20
→
→
v ⋅ nE = 0
b)
3
3
3
c)
4
Flugrichtung ist parallel zur Ebene E,
d.h. Flug erfolgt im gleichem Abstand zur Ebene E
Berechnen des Gradmaßes des Winkels für die Kursänderung, z. B.:
→ →
289
⇒
α ≈ 7,2°
cos α = cos ∠( v , a ) =
209 406
Berechnen des Gradmaßes des Winkels unter dem der Landeanflug zur Horizontalebene erfolgt, z. B.:
→
→
−1
⇒
β ≈ 2,8°
sin β = sin ∠( a , n xy ) =|
|
406
Angeben einer Gleichung der Geraden sowie Berechnen der Koordinaten des
Punktes L, z. B.:
 − 14 
 18 
→




g:
x =  7 + s  − 9

 − 1
1



⇒
0=1–s
⇒
s=1
L ∈ g ∧ L ∈ Exy
⇒ L(4 | –2 | 0)
Zeigen, dass das Flugzeug im ersten Viertel der Landebahn aufsetzt, z. B.:
 15 


 4 
4


 2
→
15 
1
+ t L  − 1 gilt für tL =
(1) OL =  − 2  =  −
⇒ L liegt auf der Landebahn
 0  8 
 0
8
  



 0 


 18 
 2


 
→
1
∧
0≤t≤1
∧
0 < tL <
(2) a ′ =  − 9  ↑↑  − 1
4
 0
 0


 
⇒
20
⇒
L liegt im ersten Viertel der Landebahn.
Gebiet G 3
Aufgabe
a)
Aufgabe 3.1
Stochastik
BE Hinweise, Lösungen
2
Begründen der Wahrscheinlichkeiten, z. B.:
Zufallsexperiment mit (relativ) großem Stichprobenumfang,
Stabilwerden der relativen Häufigkeiten; relative Häufigkeiten als Näherungswerte für
Wahrscheinlichkeiten
(Empirisches Gesetz der großen Zahlen)
5
Ermitteln der Wahrscheinlichkeiten, z. B.:
P(E1) = 0,075
P(E2) = P(A ∩ B) = P(A) · P(B) = 0,00585
P(E3) = P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
= P(A) + P(B) – P(A) · P(B) = 0,14715
b)
3
Ermitteln der Wahrscheinlichkeit, z. B.:
Zufallsgröße XM: Anzahl der Pkws mit Mangel C; XM ~ B100; 0,05
P(XM ≤ 6) = B100; 0,05({0; 1; …; 6}) = 0,76601
c)
5
Berechnen des Erwartungswertes, Prüfen der Nullhypothese und Entscheidung, z. B.:
E(X) = n · p = 100 · 0,05 = 5
1 – B100; 0,05 ({0; 1; …; k – 1}) ≤ 0,05 ⇔ B100; 0,05 ({0; 1; …; k – 1}) ≥ 0,95
⇒ k – 1 = 9; k = 10;
A = {10; 11; …; 100}
Die TÜV-Station kann H0 nicht ablehnen, da 6 < 10 bzw. 6 ∉ A .
15
Gebiet G 3
Aufgabe
Aufgabe 3.2
Stochastik
BE
Hinweise, Lösungen
2
Beschreiben des Ereignisses, z. B.:
Es keimen mehr als 29, höchstens aber 45 Samenkörner.
5
Berechnen der Wahrscheinlichkeiten, z. B.:
X ~ B50; 0,8
P( X > 40 ) = 1 – P( X ≤ 40 ) = 1 – 0,5563 = 0,4437
P( X ≥ 45 ) = 1 – P( X ≤ 44 ) = 1 – 0,9520 = 0,0480
b)
3
Berechnen der Wahrscheinlichkeit für die Keimfähigkeit, z. B.:
P( Xp = 50 ) ≥ 0,5 ⇔
p50 ≥ 0,5 ⇔ p ≥ 0,986
c)
5
Berechnen der Wahrscheinlichkeit, z. B.:
Y: „Anzahl der blühenden Pflanzen“
a)
n = 1250; p = 0,9; µ = 1125; σ = 112,5
 1125 − 1125 + 0,5 
 = 0,48
P( Y > 1125 ) = 1 – P( Y ≤ 1125 ) ≈ 1 – Φ


112,5


15

KULTUSMINISTERIUM DES LANDES SACHSEN

Transcription

Similar documents

KULTUSMINISTERIUM DES LANDES SACHSEN

SCHRIFTLICHE ABITURPRÜFUNG 2010 Mathematik

Aufgaben mit Lösungen

Algebra

CAS

s vt dt Der Modellierungskreislauf

2006 LK NT

b - Leuphana Universität Lüneburg

Aufgaben zu - Lehrer-Uni

Abituraufgabe 2012 Sachsen-Anhalt Grundkurs - Mathe

Fachhochschule Jena University of Applied Sciences - EAH-Jena

Mathematik 2 - Jörn Loviscach