Abituraufgabe 2012 Sachsen-Anhalt Grundkurs - Mathe

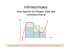
Sachsen-Anhalt: Abitur 2012 Grundkurs
www.mathe-aufgaben.com
_________________________________________________________________________________
Abituraufgabe 2012 Sachsen-Anhalt
Grundkurs
Pflichtaufgabe1 Analysis
Hilfsmittel: nicht grafikfähiger Taschenrechner
Gymnasium
Alexander Schwarz
www.mathe-aufgaben.com
Dezember 2013
1
Sachsen-Anhalt: Abitur 2012 Grundkurs
www.mathe-aufgaben.com
_________________________________________________________________________________
Gegeben sind die Funktionen f und g durch
8
(4x 3 − x 4 ) , x ∈
11
g : y = g(x) = (4 − x)e x ,
x ∈
f : y = f(x) =
Die Graphen dieser Funktionen seien F bzw. G.
a) Berechnen Sie die Nullstellen und die lokalen Extremstellen der Funktion f.
b)
Begründen Sie, dass der Graph G
für x < 0 die x-Achse nicht
schneidet.
Zeigen Sie, dass der Punkt P(3/20)
kein Hochpunkt des Graphen G ist.
Der Graph G besitzt genau einen
Wendepunkt. Berechnen Sie
dessen Koordinaten.
In der Abbildung sind Ausschnitte
der Graphen F und G dargestellt.
Geben Sie an, welche der Kurven
zum Graphen F und welche zum
Graphen G gehört.
c) Weisen Sie nach, dass die Funktion h mit y = h(x) = (5 − x)e x , x ∈

eine Stammfunktion von g ist.
Die Graphen F und G, die y-Achse und die Gerade mit der Gleichung x = 3
schließen eine Fläche vollständig ein.
Berechnen Sie mithilfe des Hauptsatzes der Differential- und Integralrechnung die
Maßzahl des Inhalts dieser Fläche.
d) Die Funktion f beschreibe im Intervall [0;3] die Bewegung eines Körpers.
Ihr Argument x entspricht der Zeit (eine Abszisseneinheit beträgt 60 Sekunden).
Der Funktionswert y entspricht dem zurückgelegten Weg (eine Ordinateneinheit
beträgt 100 Meter).
Ermitteln Sie aus der grafischen Darstellung der Funktion f näherungsweise die
Zeit, zu der der Körper die maximale Geschwindigkeit hat, und berechnen Sie
mithilfe dieses Näherungswertes die maximale Geschwindigkeit.
Begründen Sie jeweils Ihr Vorgehen.
2
Sachsen-Anhalt: Abitur 2012 Grundkurs
www.mathe-aufgaben.com
_________________________________________________________________________________
Lösungen
a) Nullstellen der Funktion f: f(x) = 0
8
8
(4x 3 − x 4 ) = 0 ⇔ ⋅ x 3 ⋅ ( 4 − x ) = 0
11
11
Mit dem Satz vom Nullprodukt folgt: x = 0 und x = 4
Die Nullstellen von f(x) sind x = 0 und x = 4.
Extremstellen der Funktion f: f ′(x) = 0 und f ′′(x) ≠ 0
f ′(x) =
8
⋅ 12x 2 − 4x 3
11
(
)
und f ′′(x) =
8
⋅ 24x − 12x 2
11
(
)
8
8
⋅ 12x 2 − 4x 3 = 0 ⇔ ⋅ x 2 ⋅ (12 − 4x ) = 0
11
11
(
)
Mit dem Satz vom Nullprodukt folgt: x = 0 und x = 3.
8
⋅ ( −36) < 0 also relatives Maximum bei x = 3
11
f ′′(0) = 0 keine Aussage möglich, Kontrolle mit Vorzeichenwechsel erforderlich
f ′′(3) =
f ′( −1) =
8
⋅ 16 > 0
11
und f ′(1) =
8
⋅8 > 0
11
Es existiert kein VZW von f ′(x) beim Durchgang durch x = 0.
Damit existiert bei x = 0 keine Extremstelle (sondern ein Sattelpunkt).
b) Begründung, dass G für x < 0 die x-Achse nicht schneidet:
Es ist g : y = g(x) = (4 − x)e x
Für alle x < 0 ist der erste Faktor 4 - x > 0 und der zweite Faktor
.
Somit ist g(x) > 0 für alle x < 0. Der Graph G verläuft für x < 0 folglich oberhalb der
x-Achse und kann die x-Achse nicht schneiden.
Nachweis, dass P(3/20) kein Hochpunkt von G ist:
Zu prüfen ist zunächst, ob der Punkt P(3/20) auf dem Schaubild von g(x) liegt:
Einsetzen von P: 20 = (4 − 3) ⋅ e3 ⇔ 20 = e3 dies ist ein Widerspruch, da e3 ≃ 20,086
Somit kann P(3/20) kein Hochpunkt von G sein.
Berechnung des Wendepunktes von G: g′′(x) = 0 und g′′′(x) ≠ 0
g′(x) = −1⋅ e x + (4 − x) ⋅ e x = e x (3 − x) (Produktregel)
g′′(x) = e x ⋅ ( −1) + e x (3 − x) = e x ⋅ (2 − x) (Produktregel)
3
Sachsen-Anhalt: Abitur 2012 Grundkurs
www.mathe-aufgaben.com
_________________________________________________________________________________
g′′(x) = 0 ⇔ e x (2 − x) = 0
Mit dem Satz vom Nullprodukt folgt x = 2.
Da gemäß der Aufgabenstellung ein Wendepunkt existiert, muss die hinreichende
Bedingung nicht mehr geprüft werden.
Der Wendepunkt lautet W(2 / g(2)) = W(2 / 2e2 )
Zuordnung der Schaubilder zu den Funktionen:
K 2 verläuft durch den Ursprung O(0/0). Der Ursprung liegt nur auf dem Schaubild F von
f(x), da f(0) = 0 gilt. Im Gegensatz hierzu gilt g(0) = 4.
K 2 entspricht dem Schaubild F und K1 entspricht dem Schaubild G.
c) Nachweis, dass h(x) eine Stammfunktion von g(x) ist:
Der Nachweis erfolgt durch Berechnung von h′(x) :
h′(x) = −1⋅ e x + (5 − x) ⋅ e x = e x ⋅ ( −1 + 5 − x) = e x (4 − x) = g(x)
Es ist h′(x) = g(x) und damit ist h(x) eine Stammfunktion von g(x).
Berechnung der Fläche:
3
3
8

x
3
4
∫0 (g(x) − f(x))dx = ∫0 ( 4 − x ) ⋅ e − 11 ⋅ 4x − x
(
)dx
3

8 
1 
8
= ( 5 − x ) ⋅ e x − ⋅  x 4 − x 5   = 2e3 − ⋅ 32,4 − 5 ≈ 11,6 FE
11 
5 0
11

d) Die maximale Geschwindigkeit wird zu dem Zeitpunkt erreicht, bei dem das Schaubild
von f(x) die größte Tangentensteigung besitzt.
Die größte Tangentensteigung ergibt sich anschaulich an der Stelle x = 2 (also nach
120 Sekunden).
Berechnung der maximalen Geschwindigkeit:
Es ist f ′(x) =
8
8
100m
m
⋅ 12x 2 − 4x 3 mit f ′(2) = ⋅ (48 − 32) ⋅
≈ 19,4
11
11
60s
s
(
)
4