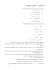הצבר הקנוני

‫הצבר הקנוני‬
‫‪30.4.15‬‬
‫‪1‬‬
‫הצבר הקנוני‬
‫נעבוד בצבר הקנוני כדי לתאר מערכת שבה הטמפרטורה ‪ ,T‬מספר החלקיקים ‪ N‬והנפח ‪ V‬קבועים‪ .‬ניתן לשמור‬
‫על טמפרטורה קבועה במערכת על ידי צימודה למאגר חום בטמפרטורה ‪ .T‬אנרגיה יכולה לעבור בינה לבין מאגר‬
‫החום ולכן הטמפרטורות שלהם משתוות‪ .‬למאגר חום מושלם קיבול חום אינסופי‪ ,‬ולכן כאשר האנרגיה שלו משתנה‬
‫כתוצאה ממעבר אנרגיה בינו לבין המערכת‪ ,‬הטמפרטורה שלו נותרת ללא שינוי‪.‬‬
‫המערכת ‪ +‬מאגר החום מהווים מערכת סגורה‪ ,‬כלומר מיקרוקנונית‪ .‬בשיווי משקל‪ ,‬האנטרופיה של המערכת‬
‫הכוללת )מערכת‪+‬מאגר( מקסימלית‪ .‬ניתן להראות שמקסימום אנטרופיה במערכת הכוללת שקול למינימום של‬
‫האנרגיה החופשית של הלמהולץ עבור המערכת )הנמצאת בטמפרטורה קבועה‪ ,‬כלומר בצבר הקנוני(‪ .‬לכן במערכת‬
‫בצבר הקנוני‪ ,‬בשיווי משקל האנרגיה החופשית של הלמהולץ ‪ F = E − T S‬מינימלית‪ .‬משמעות הדבר היא‬
‫שבטמפרטורה אפס ‪ F = E‬ולכן האנרגיה מינימלית‪ ,‬ואילו בטמפרטורה גבוהה‪ F ≈ −T S ,‬ולכן האנטרופיה‬
‫מקסימלית‪.‬‬
‫‪−βEi‬‬
‫הקנוני‬
‫בצבר‬
‫ההסתברות למצוא את המערכת במצב מיקרוסקופי ספציפי ‪ i‬עם אנרגיה ‪ Ei‬היא ‪,P (i) = e Z‬‬
‫‪P‬‬
‫= ‪ Z‬היא פונקצית החלוקה הקנונית )המסומנת גם ‪ ,(QN‬ו־ ‪.β = kB1T‬‬
‫כאשר ‪e−βEi‬‬
‫‪i∈states‬‬
‫פתרון בעיות בצבר הקנוני‪:‬‬
‫‪ .1‬מחשבים את פונקצית החלוקה ‪e−βEi‬‬
‫‪P‬‬
‫=‪.Z‬‬
‫‪i∈states‬‬
‫‪ .2‬מפונקצית החלוקה ניתן לחשב את‪:‬‬
‫)א( האנרגיה החופשית‪F = − β1 log Z :‬‬
‫∂‬
‫‪= − ∂β‬‬
‫)ב( האנרגיה‪(log Z) :‬‬
‫∂‬
‫) ‪∂β (βF‬‬
‫=‪E‬‬
‫‪2 ∂F‬‬
‫‪S = − ∂F‬‬
‫)ג( האנטרופיה‪∂T = kB β ∂β :‬‬
‫‪= −kB β 2 ∂E‬‬
‫)ד( קיבול החום‪∂β :‬‬
‫‪2‬‬
‫‪∂E‬‬
‫‪∂T‬‬
‫= ‪CV‬‬
‫מערכת שני מצבים בצבר הקנוני‬
‫נחזור לדון במערכת של ‪ N‬חלקיקים ברי הבחנה שלכל אחד מהם שני מצבים‪ :‬מצב ‪ 0‬לו אנרגיה ‪ ,0‬ומצב ‪ 1‬לו‬
‫אנרגיה ‪ .‬כעת נחקור אותה בצבר הקנוני‪.‬‬
‫נסמן ב‪ si ∈ 0, 1‬את מצב החלקיק ה־‪ .i‬נשים לב שאנרגית החלקיק ה־‪ i‬היא ‪.Ei = si‬‬
‫ראשית‪ ,‬פונקצית החלוקה החד־חלקיקית‪:‬‬
‫‪e−βs1 = 1 + e−β‬‬
‫‪X‬‬
‫= ‪Z1‬‬
‫‪s1 =0,1‬‬
‫ההסתברות של חלקיק להיות במצב ‪ ,P (0) = Z11 :0‬ההסתברות של חלקיק להיות במצב ‪:1‬‬
‫‪N‬‬
‫‪P‬‬
‫=‪H‬‬
‫בחזרה למערכת של ‪ N‬חלקיקים‪ .‬ההמילטוניאן של המערכת‪si :‬‬
‫‪i=1‬‬
‫‪1‬‬
‫‪e−β‬‬
‫‪Z1‬‬
‫= )‪.P (1‬‬
‫פונקצית החלוקה של המערכת‪:‬‬
‫‪N‬‬
‫‪= Z1N = 1 + e−β‬‬
‫‪N‬‬
‫‪e−βs1‬‬
‫‪ X‬‬
‫‪si‬‬
‫=‬
‫‪N‬‬
‫‪P‬‬
‫‪−β‬‬
‫‪e‬‬
‫‪i=1‬‬
‫‪s1 =0,1‬‬
‫‪X‬‬
‫=‪Z‬‬
‫} ‪{si‬‬
‫האנרגיה החופשית‪:‬‬
‫‬
‫‪1‬‬
‫‪N‬‬
‫‪log Z = − log 1 + e−β‬‬
‫‪β‬‬
‫‪β‬‬
‫‪F =−‬‬
‫האנרגיה הפנימית‪:‬‬
‫‪e−β‬‬
‫‪1‬‬
‫)‪∂(log Z‬‬
‫‪= N‬‬
‫‪= N β‬‬
‫‪∂β‬‬
‫‪1 + e−β‬‬
‫‪e +1‬‬
‫‪E=−‬‬
‫‪∂S‬‬
‫‪. T1 = ∂E‬‬
‫ניתן להפוך את הקשר ולקבל את )‪ T (E‬־ הזהה לביטוי שחישבנו בצבר המיקרוקנוני מתוך‬
‫מכיוון ש־ ‪ ,E = N1‬כאשר ‪ N1‬הוא מספר החלקיקים הממוצע ברמה העליונה‪ ,‬מהאנרגיה הפנימית הממוצעת‬
‫‪e−β‬‬
‫‪ .N1 = E = N 1+e‬לחילופין‪ ,‬ניתן היה לחשב את ‪ N1‬מתוך )‪ P (1‬שחושב קודם‪:‬‬
‫שחישבנו ניתן להסיק ש‪−β :‬‬
‫מכיוון שאין אינטראקציה בין החלקיקים והם בלתי תלויים‪ ,‬מספר החלקיקים הממוצע ברמה העליונה שווה‬
‫למספר החלקיקים הכולל כפול ההסתברות שחלקיק בודד נמצא ברמה העליונה‪:‬‬
‫‪e−β‬‬
‫‪1 + e−β‬‬
‫‪N1 = N P (1) = N‬‬
‫בגבול של טמפרטורות נמוכות ‪ .E → 0 :(β → ∞) T → 0‬כל החלקיקים נמצאים במצב ‪ 0‬־ המערכת במצב‬
‫עם אנרגיה מינימלית‪.‬‬
‫בגבול של טמפרטורות גבוהות ∞ → ‪ ,E → 12 N :(β → 0) T‬כלומר חצי מהחלקיקים נמצאים ברמת‬
‫האנרגיה הגבוהה וחצי בנמוכה‪ .‬כפי שראינו בתרגול שעבר‪ ,‬זהו המצב של מקסימום אנטרופיה )בו למערכת מספר‬
‫רב ביותר של מצבים מיקרוסקופיים(‪.‬‬
‫קיבול החום‪:‬‬
‫‪∂E‬‬
‫‪∂E‬‬
‫‪eβ‬‬
‫‪= −β 2 kB‬‬
‫‪= kB N β 2 2 β‬‬
‫‪∂T‬‬
‫‪∂β‬‬
‫‪(e + 1)2‬‬
‫‪2‬‬
‫= ‪CV‬‬
‫בגבולות של טמפרטורות נמוכות וגבוהות קיבול החום שואף לאפס‪ .‬בטמפרטורה נמוכה רוב החלקיקים נמצאים‬
‫ברמת היסוד‪ .‬כל עוד << ‪ ,kB T‬שינויים בטמפרטורה לא גורמים לשינוי גדול באנרגיה‪ .‬בטמפרטורות גבוהות‪,‬‬
‫כמעט חצי מהחלקיקים ברמת האנרגיה הגבוהה‪ .‬לא נותרו הרבה חלקיקים ברמת האנרגיה הנמוכה שיכולים‬
‫לעבור לגבוהה עם העלאת הטמפרטורה‪ ,‬ולכן השינוי באנרגיה כאשר מגדילים את הטמפרטורה קטן‪ .‬קיבול החום‬
‫מקסימלי כאשר ‪ , ∼ kB T‬אז העלאה של הטמפרטורה גורמת לחלקיקים רבים לבצע את הקפיצה הדרושה של ‬
‫באנרגיה על מנת לעבור מהרמה התחתונה לרמה העליונה‪.‬‬
‫‪3‬‬
‫דרגות חופש פנימיות בגז אידיאלי בצבר הקנוני‬
‫עד כה דיברנו על גז אידאלי המורכב מיחידות אטומיות‪ ,‬כלומר התעלמנו מהמצבים הפנימיים של יחידות הגז‬
‫)מולקולות באופן כללי(‪ .‬בתרגול זה נראה מה ההשפעה של דרגות חופש פנימיות בדידות‪ .‬אלה מופיעות כאשר‬
‫מתייחסים למולקולות כאובייקטים קוונטיים‪ ,‬ולכן המצבים האפשריים שלהן ־ ורמות האנרגיה המתאימות ־‬
‫מקוונטטים‪ .‬החשיבות של חשבון זה הוא עמוק יותר מהסבר של ניסויים מסויימים ־ קלאסית יש רצף של מצבים‬
‫פנימיים מסוגים שונים )כגון מרחק בין אטומים במולקולה‪ ,‬מיקום האלקטרונים באטום‪ ,‬מיקום חלקי גרעין האטום‬
‫אחד ביחס לשני(‪ ,‬ולכן לפי חוק החלוקה השווה דרגות חופש פנימיות אלה אמורות לתרום הרבה מאוד לאנרגיה‬
‫הפנימית והחישובים שעשינו עבור גז אידאלי אינם רלבנטיים‪ .‬העובדה שהמצבים ורמות האנרגיה בדידים ־ בגלל‬
‫מכניקת הקוונטים ־ מסבירה‪ ,‬כפי שנראה בתרגול‪ ,‬מדוע לא צריך לקחת בחשבון את כל דרגות החופש בחשבון‬
‫)ואילו דרגות חופש כן צריך(‪.‬‬
‫‪3.1‬‬
‫פונקציית החלוקה של גז אידאלי קנוני‬
‫נזכר ראשית כיצד מחשבים את פונקציית החלוקה של גז אידאלי בצבר הקנוני‪ .‬ההימלטוניאן של גז אידאלי הוא‬
‫‪P p2i‬‬
‫= ‪ H‬ולכן פוקציית החלוקה מתקבלת על ידי‬
‫כרגיל ‪2m‬‬
‫‪i‬‬
‫ˆ‬
‫)‪dp3N dq 3N e−βH(p,q‬‬
‫)‪(1‬‬
‫‪1‬‬
‫‪N !h3N‬‬
‫"‬
‫‪#‬‬
‫∞ ˆ‬
‫‪N‬‬
‫‪p2i,j‬‬
‫‪VN Y Y‬‬
‫‪dpi,j exp −β‬‬
‫∞‪N !h3N i=1 j=x,y,z −‬‬
‫‪2m‬‬
‫‪r‬‬
‫‪N‬‬
‫‪VN Y Y‬‬
‫‪2πm‬‬
‫‪3N‬‬
‫‪N !h i=1 j=x,y,z‬‬
‫‪β‬‬
‫‬
‫‬
‫‪ N‬‬
‫‪3N/2‬‬
‫‪V N 2πm‬‬
‫‪1‬‬
‫‪V‬‬
‫≡‬
‫‪N ! h2 β‬‬
‫‪N ! λ3T‬‬
‫‪3‬‬
‫=‬
‫=‬
‫=‬
‫=‬
‫‪Z‬‬
‫כאשר הגדרנו את אורך הגל התרמי‬
‫‪h2 β‬‬
‫‪h‬‬
‫√=‬
‫‪2πm‬‬
‫‪2πmkB T‬‬
‫‪r‬‬
‫≡ ‪λT‬‬
‫בהנתן פונקציית החלוקה‪ ,‬אפשר למצוא את האנרגיה החופשית‬
‫ ‪ 2‬‬
‫‬
‫ ‬
‫‪3‬‬
‫‪h β‬‬
‫‪V‬‬
‫‪− log‬‬
‫‪+1‬‬
‫‪F = −kB T log Z = −N kB T log‬‬
‫‪N‬‬
‫‪2‬‬
‫‪2πm‬‬
‫וממנה אפשר לגזור את הגדלים הפיסיקליים המעניינים כמו למשל אנרגיה ממוצעת‬
‫)‪∂ (log Z‬‬
‫) ‪∂ (βF‬‬
‫=‬
‫‪∂β‬‬
‫‪∂β‬‬
‫‪3N‬‬
‫‪3‬‬
‫‪= N kB T‬‬
‫‪2β‬‬
‫‪2‬‬
‫‪−‬‬
‫=‬
‫‪E‬‬
‫=‬
‫ואת קיבול החום‬
‫‪3‬‬
‫‪∂E‬‬
‫‪= N kB‬‬
‫‪∂T‬‬
‫‪2‬‬
‫‪3.2‬‬
‫= ‪CV‬‬
‫דרגת חופש פנימית עם שני מצבים‬
‫כעת נניח שלכל מולקולה בגז יש שני מצבים אפשריים אשר נבדלים זה מזה באנרגיה ב )לדוגמה‪ ,‬מצבים שונים‬
‫עבור האלקטרונים‪ ,‬או קונפורמציות שונות של המולקולה(‪ .‬כלומר‪ ,‬ההמילטוניאן ניתן על ידי‬
‫‪si‬‬
‫‪N‬‬
‫‪X‬‬
‫‪i=1‬‬
‫‪+‬‬
‫‪N‬‬
‫‪X‬‬
‫‪|pi |2‬‬
‫‪2m‬‬
‫=‪H‬‬
‫‪i=1‬‬
‫כאשר ‪ si‬הוא משתנה בינארי )שווה ‪ 0‬או ‪ (1‬המסמל אם המולקולה ה‪ i‬נמצאת במצב הנמוך יותר אנרגטית )‪(si = 0‬‬
‫או במצב הגבוה יותר אנרגטית )‪ .(si = 1‬עתה פונקציית החלוקה תנתן על ידי הנוסחה‬
‫ˆ ‪X‬‬
‫‪1‬‬
‫)‪dp3N dq 3N e−βH(p,q,s‬‬
‫‪N !h3N s ..s‬‬
‫‪N‬‬
‫=‬
‫‪Z‬‬
‫‪1‬‬
‫הסכום הוא על כל האפשרויות של ‪ N‬המשתנים ‪ si‬להיות ‪ 0‬או ‪.1‬‬
‫חישוב פונקציית החלוקה‬
‫אם נציב את ההמילטוניאן נקבל‬
‫"‬
‫‪!#‬‬
‫ˆ ‪X‬‬
‫‪X |pi |2‬‬
‫‪X‬‬
‫‪1‬‬
‫‪3N‬‬
‫‪3N‬‬
‫=‬
‫‪dp dq exp −β‬‬
‫‪+‬‬
‫‪si‬‬
‫‪N !h3N s ..s‬‬
‫‪2m‬‬
‫‪i‬‬
‫‪i‬‬
‫‪1‬‬
‫‪N‬‬
‫(‬
‫"‬
‫( )‪#‬‬
‫"‬
‫)‪#‬‬
‫ˆ‬
‫‪X‬‬
‫‪X‬‬
‫‪X |pi |2‬‬
‫‪1‬‬
‫=‬
‫‪exp −β‬‬
‫‪si‬‬
‫×‬
‫‪dp3N dq 3N exp −β‬‬
‫)‪(2‬‬
‫‪3N‬‬
‫‪N‬‬
‫‪!h‬‬
‫‪2m‬‬
‫‪s ..s‬‬
‫‪i‬‬
‫‪i‬‬
‫‪N‬‬
‫‪4‬‬
‫‪1‬‬
‫‪Z‬‬
‫איור ‪ :1‬קיבול החום כפונקצייה של טמפרטורה בגז אידאלי עם דרגת חופש פנימית )‪ (a‬בינארית )שני מצבים(; )‪(b‬‬
‫עם ‪ n = 10‬מצבים ו )‪ (c‬עם ∞ מצבים‬
‫כלומר‪ ,‬פונקציית החלוקה היא מכפלה של פונקציית חלוקה של גז אידאלי ושל מערכת שני המצבים‪ .‬התפרקות‬
‫פונקציית החלוקה למכפלה של של פונקציות חלוקה על תת מערכות )שבמקרה זה שתיהן מוגדרות על אותם‬
‫‪ N‬חלקיקים!( נובעת מחוסר האינטראקציה בהמילטוניאן בין המערכות‪ ,‬ולכן הינה כללית )תחת הנחת חוסר‬
‫אינטראקציה(‪ .‬אילו היינו עובדים בצבר המיקרוקנוני היינו רואים ששם אי אפשר לרשום את מספר המצבים בתור‬
‫מכפלה )בדיוק( של איבר המתאים לגז אידאלי ואיבר המתאים לדרגת החופש הפנימית‪ ,‬ולכן החשבון קשה יותר ־‬
‫זה )אי התלות בין "חלקי" המערכת( הוא היתרון החישובי של האנסמבל הקנוני על פני המיקרוקנוני‪.‬‬
‫הסכום ב)‪ (2‬מחושב כ‬
‫"‬
‫‪#‬‬
‫‪!N‬‬
‫‪X‬‬
‫‪X‬‬
‫‪X‬‬
‫‪exp −β‬‬
‫‪si‬‬
‫=‬
‫] ‪exp [−βs1‬‬
‫‪s1 =0,1‬‬
‫‪N‬‬
‫)‪(3‬‬
‫)]‪(1 + exp [−β‬‬
‫‪s1 ..sN‬‬
‫‪i‬‬
‫=‬
‫הסכום הזה הוא פונקצית החלוקה של מערכת ‪ 2‬רמות‪ ,‬אותה חישבנו קודם‪.‬‬
‫ואם נשתמש בתוצאה )‪ (1‬מהסעיף הקודם נקבל‬
‫‪N‬‬
‫)‪(4‬‬
‫‪1 + e−β‬‬
‫‪N‬‬
‫‪V‬‬
‫‪λ3T‬‬
‫‬
‫‪1‬‬
‫!‪N‬‬
‫=‪Z‬‬
‫קיבול חום‬
‫עתה נמצא את האנרגיה החופשית וקיבול החום‬
‫‪−kB T log Z‬‬
‫ ‬
‫ ‪ 2‬‬
‫‬
‫‬
‫‪V‬‬
‫‪3‬‬
‫‪h β‬‬
‫‪−β‬‬
‫‪−N kB T log‬‬
‫‪− log‬‬
‫‪+ 1 + log 1 + e‬‬
‫‪N‬‬
‫‪2‬‬
‫‪2πm‬‬
‫ולכן האנרגיה הממוצעת היא‬
‫) ‪∂ (βF‬‬
‫‪∂β‬‬
‫‪3‬‬
‫‪e−β‬‬
‫‪N kB T + N‬‬
‫‪2‬‬
‫‪1 + e−β‬‬
‫‪5‬‬
‫=‬
‫=‬
‫‪E‬‬
‫=‬
‫=‬
‫‪F‬‬
‫וקיבול החום הוא‬
‫‬
‫‪−β‬‬
‫‪+ 2 e−2β‬‬
‫‪−2 e−β 1 + e‬‬
‫‪3‬‬
‫‪N kB + N‬‬
‫‪2‬‬
‫=‬
‫‪3‬‬
‫‪e−β‬‬
‫‪N kB + N kB β 2 2‬‬
‫‪2‬‬
‫‪2‬‬
‫) ‪(1 + e−β‬‬
‫=‬
‫‪2‬‬
‫) ‪(1 + e−β‬‬
‫)‪(5‬‬
‫‬
‫‪∂β‬‬
‫‪∂T‬‬
‫‬
‫‪CV‬‬
‫‪∂β‬‬
‫‪. ∂T‬‬
‫כאשר השתמשנו בעובדה ש ‪= − kB1T 2 = −kB β 2‬‬
‫הבה ננתח את התנהגות קיבול החום עבור טמפרטורות נמוכות וגבוהות‪ :‬עבור ‪ β → ∞ ,T → 0‬ולכן‬
‫‪ e−β → 0‬ואנו מקבלים ‪ .CV (T → 0) → 23 N kB‬עבור ∞ → ‪ β → 0 ,T‬ולכן ‪ e−β → 1‬ואנו מקבלים‬
‫‪ .CV (T → ∞) → 32 N kB‬האם מכאן ניתן ללמוד שדרגות החופש הפנימיות לא משפיעות? אם מציירים במחשב‬
‫את קיבול החום כפונקציה של טמפרטורה‪ ,‬כמו באיור ‪ ,1a‬מקבלים מקסימום באזור הערך ‪ .β ∼ 1‬ההתנהגות‬
‫הלא מונוטונית של קיבול החום נקראת "אנומליית שוטקי" והיא נמדדה ניסויית )בעיקר במוצקים ולא בגזים‪ ,‬אבל‬
‫הסיבה היא זהה(‪ .‬מקסימום צר של קיבול החום משמעו דרגות חופש חסומות )כלומר‪ ,‬עם אנרגיה מקסימלית( שלא‬
‫מעוררות מתחת לטמפרטורה מסויימת‪ ,‬ורוויות מעל לטמפרטורה אחרת‪ .‬מכאן אפשר ללמוד שבחשבון יש לקחת‬
‫רק דרגות חופש רלבנטיות‪ ,‬כלומר שהאנרגיה שלהן ‪ , ∼ kB T‬ודרגות חופש עם אנרגיה גדולה בהרבה או קטנה‬
‫בהרבה אפשר להזניח‪.‬‬
‫חישוב בצבר המיקרו קנוני‬
‫מלבד הרלבנטיות הפיסיקלית של מערכת זו‪ ,‬זו גם דוגמה הממחישה את היתרון של הצבר הקנוני על פני‬
‫המיקרוקנוני‪.‬‬
‫‪4‬‬
‫‪4.1‬‬
‫דרגת חופש פנימית בדידה‬
‫מולקולה עם ‪ n‬מצבים פנימיים‬
‫אילו למולקולת הגז היו ‪ n‬מצבים אפשריים במקום רק שניים )אם לוקחים בחשבון עוד רמות אנרגיה אפשריות‪,‬‬
‫או יותק קונפורציות של המולקולה(‪ ,‬כל שהיה משתנה הוא שהסכום )‪ (3‬היה על ‪ n‬המצבים‪ .‬לשם הפשטות נניח‬
‫שהאנרגיה של המצב ה‪ k‬היא ‪ .k‬אז‬
‫]‪1 − exp [−βn‬‬
‫]‪1 − exp [−β‬‬
‫=‬
‫] ‪exp [−βs1‬‬
‫‪n−1‬‬
‫‪X‬‬
‫‪s1 =0‬‬
‫ולכן פונקציית החלוקה היתה‬
‫‪N‬‬
‫)‪(6‬‬
‫]‪1 − exp [−βn‬‬
‫]‪1 − exp [−β‬‬
‫ ‪N‬‬
‫‪V‬‬
‫‪λ3T‬‬
‫‬
‫‪1‬‬
‫!‪N‬‬
‫=‪Z‬‬
‫אם נחשב את קיבול החום כעת נקבל כמו באיור ‪ ,1b‬שרוחב המקסימום גדל מכיוון שיש תחום גדול יותר של‬
‫טמפרטורות עבורו יש רמות חדשות לעורר‪ .‬עם זאת‪ ,‬עבור טמפרטורה גבוהה מספיק קיבול החום יחזור לערך של‬
‫גז אידאלי רגיל )כלומר‪ ,‬נראה אנומליית שוטקי(‪.‬‬
‫‪4.2‬‬
‫מולקולה עם ∞ מצבים פנימיים‬
‫באותה שיטה ניתן לחשב את קיבול החום כאשר יש אינסוף מצבים עבור דרגת החופש הפנימית )עם הפרש אנרגיה‬
‫קבוע (‪ .‬זהו המצב עבור מולקולה דו אטומית שממודלת כקפיץ קוונטי‪ .‬במצב כזה הסכום יהיה‬
‫‪6‬‬
‫‪1‬‬
‫]‪1 − exp [−β‬‬
‫] ‪exp [−βs1‬‬
‫=‬
‫∞‬
‫‪X‬‬
‫‪s1 =0‬‬
‫ולכן‬
‫)‪(7‬‬
‫‪N‬‬
‫‪−N‬‬
‫)]‪(1 − exp [−β‬‬
‫‪V‬‬
‫‪λ3T‬‬
‫‬
‫‪1‬‬
‫=‪Z‬‬
‫!‪N‬‬
‫קיבול החום במקרה זה הוא‬
‫!‬
‫‪2‬‬
‫)‪e−β (β‬‬
‫‪3‬‬
‫‪+‬‬
‫‪2 (1 − e−β )2‬‬
‫‪CV = N kB‬‬
‫והוא מופיע באיור ‪ .1c‬כפי שניתן לראות במקרה זה‪ ,‬אין מקסימום צר בקיבול החום אלא יש עלייה מונוטונית‬
‫מהערך ‪ CV = 23‬המתאים לגז אידאלי ללא דרגות חופש פנימיות‪ ,‬לערך ‪ CV = 25‬המתאים לגז אידאלי של קפיצים‬
‫)חד מימדיים‪ ,‬שאינם יכולים להסתובב ־ כמו בתרגיל הבית(‪ .‬שימו לב שהגרף מתאר התנהגות קוונטית‪ ,‬מכיוון שרק‬
‫קוונטית יש רמות אנרגיה בדידות‪ ,‬שאינן מעוררות בטמפרטורות נמוכות מספיק‪ .‬קלאסית )כפי שתמצאו בתרגיל‬
‫הבית( דרגות החופש הפנימיות )בעלות אנרגיה רציפה( מעוררות בכל טמפרטורה גדולה מאפס‪ .‬גרף מהסוג הזה‬
‫אכן נמדד בניסוי ומהווה אישוש למכניקת הקוונטים!‬
‫‪7‬‬