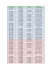יחידות `
Transcription
יחידות `
סמסטר אביב ,תשע"א )(2011
מתרגלים :רועי עשור ואמיר ונד
כימיה פיסיקלית א' ) – (69163תרגול מס' 2
החוג לכימיה
המכון לכימיה
מטרות התרגול
חלק א' – יחידות:
.1רענון נושא היחידות בתחומי הפיסיקה והכימיה.
.2אזכור של יחידות חשובות ושימושיות.
חלק ב' – משוואת הגז האידיאלי וחוק דלטון.
חלק ג' – ספקטרופוטומטריה – חוק בר-למבר.
)חלקים ב' וג' יעניינו אותנו בקורס זה כבסיס לטכניקות למדידת קצבי ריאקציות(.
חלק א' -יחידות
הקדמה או למה זה חשוב ?
יחידות הן האמצעי היחיד להעברת מידע אודות גדלים פיסיקליים ולהשוואה בין גדלים שונים .לערך
מספרי של גודל פיסיקלי אין כל משמעות ללא היחידות שלו.
לא חסרות דוגמאות )בנוסף לאלפי סטודנטים ממורמרים שאיבדו נקודות במבחנים (...מההיסטוריה
לחשיבות היחידות :מטוס שהתרסק בטרם סוף טיסתו עקב מילואו בדלק ביחידות של ק"ג ולא פאונדים
) ,(1997רכב החלל Mars Climate Orbiterשנהרס בתוך האטמוספירה של מאדים עקב תוכנות
שחישבו ביחידות שונות )פאונד-שניה ,ולא יחידות מטריות( ,ומטוס נוסף של חברת Korea Air
שהתרסק בעקבות בלבול בין הוראות מגדל הפיקוח להוראת מחוג הגובה.
בסדר ...אנחנו מקווים שהשתכנע תם שיחידות זה דבר חשוב .הבה נעשה מעט סדר בבלגאן ונזכיר למי
ששכח את חוקי העבודה עם יחידות.
מערכות יחידות נפוצות
1
במהלך ההיסטוריה היו נפוצות ברחבי העולם מערכות רבות ושונות של
יחידות ,שהקשו על התקשורת בין אנשים .מרבית היחידות בעבר
התבססו על גדלים "שימושיים" או על גדלים נפוצים מגוף האדם )ראו
באיור משמאל(.
אנו נתמקד כאן בשיטות המטריות ,שאומצו כיום כמעט בכל העולם
)פרט לארה"ב ומספר מדינות קטנות(.
1הטבלאות והאיורים שבחלק זה נלקחו מן האתר של ה,National Institute of Standards and Technology (NIST) -
בכתובת.http://www.physics.nist.gov/cuu/index.html :
כימיה פיסיקלית א' ) – (69163תרגול מס' (1) :2יחידות (2) ,משוואת הגז האידיאלי (3) ,חוק בר-למבר
1
סמסטר אביב ,תשע"א )(2011
מתרגלים :רועי עשור ואמיר ונד
החוג לכימיה
המכון לכימיה
מערכות היחידות המטריות המקוריות התבססו על שלושה גדלים פיסיקליים :אורך ,מסה ,זמן.
שתי שיטות נפוצות הן:
C G S
ւ ↓ ց
second
gram
M K S
ւ ↓ ց
centimeter
meter kilogram second
השיטה הנוהגת בעולם כיום פותחה בשנות ה 60 -בהתבסס על ה ,MKS -ומכונה )בתרגום חופשי(
"מערכת היחידות הבינלאומית" או ) SIבצרפתית.(Le Système International d'Unités :
מערכת השיטות הזו היא דינמית ומתעדכנת בהתאם לצורכי עולם המדע והמחקר ,וכמו כן מתעדכנת
מבחינת הדיוק של המידות.
מערכת ה SI -הרחיבה את סט הבסיס של יחידות ה MKS -לשבע יחידות בסיסיות:
Table 1. SI base units
SI base unit
Symbol
m
kg
s
A
K
mol
cd
Base quantity
Name
meter
kilogram
second
ampere
kelvin
mole
candela
length
mass
time
electric current
thermodynamic temperature
amount of substance
luminous intensity
מן היחידות האלו ניתן לגזור יחידות לכלל הגדלים הפיסיקליים בטבע.
חלק מן היחידות נגזרות ישירות ושומרות על שמות מקוריים של ה ;SI -למשל:
Table 2. Examples of SI derived units
SI derived unit
Name
Symbol
2
Derived quantity
m
)מ"ר( square meter
)שטח( Area
m3
)מ"ק( cubic meter
)נפח( Volume
m/s
)מטר לשניה( meter per second
)מהירות( speed, velocity
m/s2
)מטר לשניה בריבוע( meter per second squared
)תאוצה( Acceleration
m-1
reciprocal meter
)מספר גל( wave number
kg/m3
)ק"ג למ"ק( kilogram per cubic meter
)צפיפות מסה או מסה סגולית( mass density
mole/ m3
moles per cubic meter
)ריכוז( concentration
כימיה פיסיקלית א' ) – (69163תרגול מס' (1) :2יחידות (2) ,משוואת הגז האידיאלי (3) ,חוק בר-למבר
2
(2011) תשע"א,סמסטר אביב
החוג לכימיה
המכון לכימיה
רועי עשור ואמיר ונד:מתרגלים
: להלן כמה יחידות כאלו החשובות לקורס שלנו. חלק מן היחידות זכו לשמות מיוחדים,ולעומת זאת
Table 3. SI derived units with special names and symbols
SI derived unit
Derived quantity
Name
Symbol
Expression
Expression
in terms of
in terms of
other SI units SI base units
Frequency ( )תדירות
hertz
Hz
-
s-1
Force ()כוח
newton
N
-
m·kg·s-2
pressure, stress ()לחץ
pascal
Pa
N/m2
m-1·kg·s-2
energy, work, quantity of heat
( אנרגיה, חום,)עבודה
joule
J
N·m
m2·kg·s-2
power, radiant flux ()הספק
watt
W
J/s
m2·kg·s-3
Celsius temperature ()טמפרטורה
degree Celsius °C
Concentration ()ריכוז
molar
M
-
K
1,000 mol/m3
במספר( מכפל וחלוקה של היחידות22 ) האיור הבא מדגים כיצד ניתן לקבל את היחידות מן הסוג האחרון
:SI -הבסיסיות של ה
3
למבר-( חוק בר3) ,( משוואת הגז האידיאלי2) ,( יחידות1) :2 '( – תרגול מס69163) 'כימיה פיסיקלית א
סמסטר אביב ,תשע"א )(2011
מתרגלים :רועי עשור ואמיר ונד
החוג לכימיה
המכון לכימיה
שמות נוספים שחשוב להכיר הם הקיצורים של סדרי גודל של יחידות ,המבוססים על חזקות של 10
)בשיטה המטרית( 20 .השמות שהוגדרו ע"י ה SI -מופיעים בטבלה הבאה
Table 4. SI prefixes
Symbol
d
c
m
µ
n
p
f
a
z
y
Name
deci
centi
milli
micro
nano
pico
femto
atto
zepto
yocto
Factor
10-1
10-2
10-3
10-6
10-9
10-12
10-15
10-18
10-21
10-24
Symbol
Y
Z
E
P
T
G
M
k
h
da
Name
yotta
zetta
exa
peta
tera
giga
mega
kilo
hecto
deka
Factor
1024
1021
1018
1015
1012
109
106
103
102
101
בנוסף ,ככימאים כדאי לנו להכיר את יחידות האורך הבאות )לא חלק רשמי מה:(SI -
1 A = 10−8 cm = 10−10 m = 0.1nm
1Bohr = 1a.u. ≅ 0.53 A
מספר הערות חשובות:
נהוג לסמן יחידות בעזרת סוגריים מרובעים.[unit] :
נפח :היחידה הסטנדרטית למדידה היא ,m3אך היא לא הנפוצה בכימיה .בד"כ משתמשים בבסיס
הקשור לליטר ) ,(literומודדים ב ml,µl -וכו'.
ליטר אינו יחידה סטנדרטית )נחזור לכך כאשר נעסוק בתורת ההתנגשויות בהמשך הקורס(:
1L = 103 cm3 = 10−3 m3
.
טמפרטורה:
המעבר בין טמפרטורות קלווין )אבסולוטיות( לצלזיוס. T ( K ) = T ( C ) + 273.15 :
לחץ :בכימיה משתמשים בהרבה סוגים של יחידות לחץ ,הן בהתאמה לערך הנמדד )סדרי גודל
נכונים( והן מטעמים היסטוריים .כאמור ,היחידה התקנית לפי ה SI -היא הפסקאל.Pa ,
יחידות לחץ נפוצות השימושיות בכימיה והמעבר ביניהן:
1bar = 105 Pa
1torr = 1 mmHg
1atm = 101, 325 Pa = 1.01325 bar = 760torr
כימיה פיסיקלית א' ) – (69163תרגול מס' (1) :2יחידות (2) ,משוואת הגז האידיאלי (3) ,חוק בר-למבר
4
מתרגלים :רועי עשור ואמיר ונד
סמסטר אביב ,תשע"א )(2011
החוג לכימיה
המכון לכימיה
אנרגיה :גם באנרגיה ניתקל באוסף של יחידות הנמצאות בשימוש בכימיה ,כאשר התקנית היא
כמובן יחידת הג'אול.J ,
קשרים חשובים:
1cal = 4.184 J
1J = 107 erg
שיטה נוחה למעבר יחידות בעזרת קבוע הגזים:
J
= 0.082057 L ⋅ atm = 1.987 cal
mol ⋅ K
mol ⋅ K
mol ⋅ K
R = 8.314472
שנית ,נציין שיטה נוחה למעבר יחידות .היות ובדרך כלל זוכרים את גודלו של קבוע הגזים
לפחות בשתי מערכות יחידות )או שהוא נתון בטבלה( ,והיות וערכו הפיסיקלי של קבוע הגזים
J
שווה בכל מערכות היחידות ,ניתן לקבוע כי:
0.082 lit ⋅ atm = R = 8.314
mol ⋅ K
mol ⋅ K
השוואה בין שני הצדדים של שוויון זה תיתן את יחס ההמרה:
1J = 0.082 lit ⋅ atm ≅ 9.9 ×10 −3 lit ⋅ atm
8.314
•
מולקולות vs.מולים:
בעבודה ביחידות כימיות ,נהוג לעבוד באחד משני "בסיסים" – או הבסיס החלקיקי/מולקולרי או
הבסיס המולי ,שסופר את החלקיקים ביחידות של "מול" לפי מספר אבוגדרו:
)שימו לב – מספר אבוגדרו מכיל יחידות !!!( N av = 6.02 ×10 23 mol −1
הגודל החלקיקי
–
הגודל המולקולרי
הגודל
N
מספר
n
)כמות חלקיקים(
N = N AV ⋅ n
)כמות במולים(
mol
קבוע הגזים /
kB
J
K
)קבוע בולצמן(
קבוע בולצמן
R = kB ⋅ N AV
R
J
mol ⋅ K
)קבוע הגזים(
m
מסה
M / Mw
)מסת החלקיק(
M w = N AV ⋅ m
)מסה מולרית(
ε
אנרגיה
E
)אנרגיה(
E = N AV ⋅ ε
)אנרגיה למול(
kg
mol
↔
gr
mol
kJ
mol
↔
J
mol
כימיה פיסיקלית א' ) – (69163תרגול מס' (1) :2יחידות (2) ,משוואת הגז האידיאלי (3) ,חוק בר-למבר
5
gr ↔ kg
↔ kJ
J
סמסטר אביב ,תשע"א )(2011
מתרגלים :רועי עשור ואמיר ונד
k B = R = 1.380 ×10 −23 J
N av
K
J
mol ⋅ K
↔
החוג לכימיה
המכון לכימיה
R = 8.314472
לצורך הדיון ,נדגים מס' מעברים כאלו שנבצע בקורס:
•
משוואת הגז האידיאלי:
PV = N av n R T = Nk BT
N av
•
↔
ביטוי למהירות הממוצעת של גז-אידיאלי:
8R / N avT
8k BT
=
π M w / N av
πm
•
=v
8 RT
π Mw
↔
=v
משוואת ארהניוס )התלות של קבוע הקצב בטמפרטורה(:
E /N
= A exp − ε a
k (T ) = A exp − a av
R
/
N
T
k
T
av
B
•
PV = nRT
↔
E
k (T ) = A exp − a
RT
קצב התנגשויות בקיר בעל שטח Aעל ידי גז אידיאלי בשו"מ תרמי:
PA0
PA0 N av
PA0 N av
PA0 N av
=
=
=
2π mk BT
2π mk BT N av
2π mN av k B N avT
2π M w RT
= ZW A 0
שימו לב שבעוד מהשלוש הדוגמאות הראשונות נדמה כי לשם מעבר בין המערכות הנ"ל כל שעלינו
לעשות הוא להמיר ישירות את הגדלים זה בזה ,הדוגמה הרביעית ממחישה כי לעתים הביטויים לא יהיו
זהים לחלוטין ) תוספת או הפחתה של כפל במספר אבוגדרו וכו'(.
הדוגמה הרביעית ממחישה את החשיבות של ההבנה כיצד לעבור בין המערכות הללו.
כימיה פיסיקלית א' ) – (69163תרגול מס' (1) :2יחידות (2) ,משוואת הגז האידיאלי (3) ,חוק בר-למבר
6
סמסטר אביב ,תשע"א )(2011
מתרגלים :רועי עשור ואמיר ונד
החוג לכימיה
המכון לכימיה
תרגילים ודוגמאות )המרת יחידות(
.1יחידת הכוח הבסיסית במערכת CGSמכונה dyneויחידת האנרגיה הבסיסית מכונה .erg
•
רשום את ה erg -כמכפלה של גדלים בסיסיים במערכת ה.CGS -
ניתן לפתור במספר דרכים ,כל אחד והאינטואיציה שלו .למשל ,ניתן לצאת מן הביטוי
לאנרגיה קינטית ולזכור כי יחידותיו הן של מסה כפול מהירות בריבוע .או ,לזכור כי
עבודה )שיחידותיה כיחידות האנרגיה( מוגדרת ככוח כפול שטח.
נעזר בדרך השנייה:
= ][Mass ⋅ Acceleration ⋅ Length
Newton's 2nd Law
=
][ Energy ] = [Work ] = [ Force ⋅ Length
gr ⋅ cm
⋅ cm] =
] = [ dyne ⋅ cm] ≡ [erg
2
sec
2
•
sec 2
= [ gr ⋅ cm
מצא את יחס ההמרה מיחידות ה N) MKS -ו (J -ליחידות ה.CGS -
כאן ,הכי פשוט לצאת מן ההגדרה ולבצע את המעבר בין היחידות הבסיסיות:
kg ⋅ m
kg ⋅ m
gr
gr ⋅ cm
→
1
⋅103
⋅ (102 ) cm = 105
= 105 dyne
2
2
1kg =1,000 gr
sec
sec
sec 2
kg
1m =100 cm
m
1N = 1
2
kg ⋅ m 2
2
gr
gr ⋅ cm 2
kg ⋅ m 2
1J = 1
→
1
⋅103
⋅ (102 ) cm = 107
= 107 erg
2
2
2
1kg =1,000 gr
sec
sec
sec
kg
1m =100 cm
m
.2המר את יחידת הנפח ליטר ליחידות התקניות לפי CGSוMKS -
יחידות הנפח הסטנדרטיות מוגדרות ע"י יחידות אורך בחזקה שלישית .לפי הגדרת הליטר:
. 1lit = 1 dm3לכן נקבל:
3
1lit = 1 dm3 = 1 × (10 −1 ) m3 = 10−3 m3 = 10 −3 × (10 2 ) cm3 = 10
cm3
3
3
CGS
MKS
.3השלם את השוויונות הבאים:
nm
sec
=m
= dm
=A
= 6.2 cm
= ms
= ns
= ps
= 12 fsec
הפיתרון מבוסס על היכרות עם טבלת הקידומות של סדרי הגודל:
6.2 cm = 6.2 ×108 A = 0.62 dm = 0.062 m = 6.2 ×107 nm
12 fsec = 1.2 ×10 −2 ps = 1.2 ×10−5 ns = 1.2 ×10−11ms = 1.2 ×10−14 sec
כימיה פיסיקלית א' ) – (69163תרגול מס' (1) :2יחידות (2) ,משוואת הגז האידיאלי (3) ,חוק בר-למבר
7
מתרגלים :רועי עשור ואמיר ונד
סמסטר אביב ,תשע"א )(2011
החוג לכימיה
המכון לכימיה
חישובים מתמטיים עם ערכים פיסיקליים
כללי יסוד לשימוש ביחידות:
•
כל ערך פיסיקלי מבוטא ביחס ליחידה כלשהי המתאימה לערך זה.
אם האות Xמציינת ערך פיסיקלי כלשהו ,ו [X] -זו היחידה שלו. X = n [ X ] :
למשלt = 5sec, m = 12.6 kg :
•
יש להקפיד לרשום את היחידות ,ולהתייחס אליהן כאל משתנים נוספים במשוואה.
•
מומלץ לא לערבב בין מערכות יחידות ,ולהחליט בכל תרגיל על מערכת אחת )הנוחה ביותר
לצורך התרגיל ,כמובן( ולעבוד עמה.
•
פעולות כפל וחילוק בין ערכים פיסיקליים נעשות בנפרד על הכמויות ועל היחידות ,והן מותרות
לכל שני ערכים באשר הם.
•
פעולות חיבור וחיסור מותרות רק בין כמויות שונות של ערכים פיסיקליים זהים .אין לחבר
ולחסר בין ערכים פיסיקליים שונים.
•
היחידות של נגזרות המופיעות במשוואה הן כיחידות של חלוקה פשוטה של הגדלים )יחידת
הגודל שגוזרים חלקי היחידה של המשתנה שגוזרים לפיו(.
dx x MKS / SI m
למשל ,הנוסחה למהירות הרגעית של גוף בחד-מימד. = = :
dt t
sec
היחידות של תוצאה של אינטגרל כוללות את ההכפלה ביחידות של הדיפרנציאל עליו מבוצעת
האינטגרציה .למשל ,עבור העבודהW = ∫ F ⋅ dr ⇒ [W ] = [ F ] ⋅ [r ] = [ J ] :
•
הארגומנטים של גדלים חזקתיים/לוגריתמיים או של גדלים טריגונומטריים צריכים להיות חסרי
יחידות.
אנליזת יחידות ומימדיות של משוואה
בכל משוואה פיסיקלית ,היחידות משני צידי השוויון חייבות להיות זהות !
המונח של אנליזת יחידות ) (dimensional analysisהוא כלי שימושי מאוד בפיסיקה ובכימיה .בכלי זה,
"מתעלמים" לרגע מן הערכים הפיסיקליים שמאחורי המשוואה ובודקים את יחידותיה בלבד.
לא ניכנס כאן לעומק הנושא )זוהי תורה שלמה !( ,אך חשוב לפחות להכיר את המושג.
באמצעות כלי פשוט זה ,ניתן לעתים לבדוק סבירות של משוואות וחישובים )למשל ,ניתן להפריך בקלות
משוואה שמקבלים( ולעתים אף "מנחשים" בעזרת אמצעי זה נוסחאות שונות.
כימיה פיסיקלית א' ) – (69163תרגול מס' (1) :2יחידות (2) ,משוואת הגז האידיאלי (3) ,חוק בר-למבר
8
סמסטר אביב ,תשע"א )(2011
מתרגלים :רועי עשור ואמיר ונד
החוג לכימיה
המכון לכימיה
דוגמה לשימוש :2חלקיק במסה mנופל מגובה hאל פני כדה"א בשדה הכבידה עם gנתון
ננסה "לנחש" בצורה מושכלת נוסחה למהירות של הגוף בפוגעו בקרקע .נזכור ,כי הנוסחה שלנו
צריכה לכלול את הגדלים הידועים של הבעיה ,שהם:
מסת החלקיק ,[kg] mהגובה ,[m] hהתאוצה .[m/sec2] g
הדרך היחידה להרכיב מהירות מן הגדלים הנ"ל:
]m ⋅ m = [accelration] ⋅ [length
sec 2
= . [v ] = m
sec
ובכן ,על סמך אנליזת היחידות הפשוטה הזו ,ננחש את הקשר. v ∝ gh :
ואכן ,פיתרון מדויק של המשוואה נותן ) v = 2 ghבדקו !( – פקטור מספרי של 2בלבד.
המסקנה :במידה ובעיה נתונה אינה תלויה במספר רב מידי של פרמטרים ,ייתכן ומשיקולי מימדים
בלבד ניתן ל"נחש" את התשובה הסופית עד כדי קבוע חסר מימדים !
תרגילים ודוגמאות
.1בדקו את המימדיות של החוק השני של ניוטון.
החוק השני של ניוטון )בניסוח "תיכוני"(. F = ma :
נבדוק האם היחידות של אגף ימין אכן נותנות יחידות של כוח:
][ ma ] = [ mass ⋅ acceleration] = kg ⋅ m sec2 = [ N ] = [ force
.2בדקו את איינשטיין :האם הנוסחה המוכרת E = mc 2הגיונית מבחינת יחידות ?
למעשה ,מי שזוכר את הנוסחה לאנרגיה קינטית E = 12 mv 2אינו
צריך לבדוק דבר ,היות והוא מיד רואה את הזהות ביחידות )לפקטור
1/2אין כמובן שום משמעות כאן(.
אבל ,גם אם לא זוכרים ,ניתן לבדוק מיידית:
MKS / SI
2
= [mc 2 ] = [mass ⋅ speed 2 ] = kg ⋅ m 2
sec
m
] = kg ⋅ 2 ⋅ m = [ energy ] = [ J
sec
Newton 2nd Law:
F=ma
Work=force×length
ובכן ,שוב איינשטיין צדק )לפחות מבחינת יחידות( !
2הדוגמה נלקחה מתוך רשימותיו של פרופ' שביב לקורס "שיטות שיערוך בפיסיקה" ) ,(77412הנמצאות באתר המקוון:
./http://www.phys.huji.ac.il/~shaviv/students/77412
כימיה פיסיקלית א' ) – (69163תרגול מס' (1) :2יחידות (2) ,משוואת הגז האידיאלי (3) ,חוק בר-למבר
9
סמסטר אביב ,תשע"א )(2011
מתרגלים :רועי עשור ואמיר ונד
החוג לכימיה
המכון לכימיה
.3נתונה נוסחת ארהניוס ,המקשרת בין קבוע הקצב של ריאקציה כימית לטמפרטורה )אין צורך
להבין כעת את הנוסחה ,נגיע אליה בהמשך הקורס(:
RT
Ea
k = A ⋅ e−
energy
ידוע כי Eaהיא אנרגיית האקטיבציה לריאקציה פר מול:
mol
= ] . [ Ea
קבע משיקולי יחידות בלבד את היחידות של .RT
E
כפי שצוין לעיל ,הארגומנט של אקספוננט חייב להיות חסר יחידות. a = [unitless ] :
RT
MKS / SI
J
= [ mol
. [ RT ] = energy
היות ויחידות Eaנתונות ,ברור כי חייב להתקיים] :
mol
יחידות חשובות לקורס
בקורס אנו נעבוד עם משוואות קצב מן הצורה. v = k ⋅[conc. of A]α ⋅ [conc. of B]β ⋅ ... :
הקצב ) (vשל הריאקציה מודד את שינוי הריכוז של חומר מסוים כתלות בזמן ,ולכן יחידותיו הן ריכוז
חלקי זמן .למשל ,ביחידות מקובלות )אם כי לא סטנדרטיות לפי ה. [ v ] = M :(SI -
sec
הריכוזים עצמם יימדדו ביחידה מתאימה )במקרה זה ,(M ,ולכן היחידות של קבוע הקצב צריכות להיקבע
בהתאם על מנת להתאים למימדיות של המשוואה.
תרגיל :עבור משוואת קצב כללית מן הצורה, v = k ⋅ [conc. of A]α ⋅ [conc. of B]β ⋅ [conc. of C ]γ :
קבע את יחידותיו של הקבוע .k
פיתרון :נשים לב ,שלצורך היחידות אין הבדל בין החומרים השונים .לכן ,יהיה נוח להגדיר חזקה כללית
לריכוז )בקרוב נלמד כי חזקה זו מכונה הסדר הכללי של הריאקציה ,בעוד החזקות הפרטיות של כל חומר
מכונות הסדר החלקי של הריאקציה לפי החומר הנתון( .נסמן. n = α + β + γ :
n
לכן ,נקבל כי. v conc = k ⋅ conc.n = k [ ?] ⋅ conc.n [ conc ] :
sec
1− n M1− n
. [ k ] = conc
→
מהשוואת יחידות בין צדדי המשוואה נקבל :
sec sec
הנוסחה שקיבלנו היא כללית ,ותשמש אותנו בקורס לקביעת יחידות של קבוע קצב של כל הריאקציות
)בהנחה שהסדר הכללי שלהן ידוע(.
כימיה פיסיקלית א' ) – (69163תרגול מס' (1) :2יחידות (2) ,משוואת הגז האידיאלי (3) ,חוק בר-למבר
10
סמסטר אביב ,תשע"א )(2011
מתרגלים :רועי עשור ואמיר ונד
החוג לכימיה
המכון לכימיה
חלק ב' -משוואת הגז האידיאלי
קבלת משוואות הגז האידיאלי )קצת היסטוריה(
משוואת הגז האידיאלי היא תולדה של מספר ניסיויים שביצעו חוקרים במאות ה .17-18 -בכל הניסויים,
הרעיון היה לחקור שינוי של פרמטר תרמודינמי )טמפרטורה ,לחץ ,נפח וכו'( בודד ,תוך שמירה על שאר
הפרמטרים קבועים .מכל ניסוי נוסח חוק הקובע את היחס בין פרמטרים שונים ,והשילוב של כל השלושה
ביחד נותן את המשוואה המוכרת היום כמשוואת הגז האידיאלי ):(Ideal Gas Equation
•
חוק ) Boyleפורסם ב" :(1662 -לכמות נתונה של גז בטמפרטורה קבועה במערכת סגורה ,קיים
יחס הופכי בין הלחץ של הגז ) (Pלנפחו ) ."(Vבניסוח מתמטי , P ⋅V = const. :או. P ∝ 1 :
V
ניסוח אלטרנטיבי הוא. P1 ⋅V1 = P2 ⋅V2 = P3 ⋅ V3 = ... :
•
חוק ) Charlesפורסם ב" :(1802 -בלחץ קבוע ,הנפח של מסה נתונה של גז גדל או קטן באופן
מתכונתי באופן ישר לשינוי הטמפרטורה )במעלות קלווין(".
בניסוח מתמטי , V = const. :או . V ∝ T :ניסוח אלטרנטיביV1 ⋅ T2 = V2 ⋅ T1 :
T
•
חוק ) Gay-Lussacפורסם ב" :(1809 -בריאקציה שבה המגיבים והתוצרים הם גזיים ,ניתן
לבטא את היחס בין הנפחים של המגיבים והתוצר באמצעות מספרים שלמים קטנים".
חוק הגזים המשולב ) :(Combined Gas Lawהשילוב של כל החוקים הנ"ל ,מוביל לחוק – "במערכת
המכילה כמות נתונה של גז ,היחס בין מכפלת הנפח והלחץ לטמפרטורה היא קבוע". PV = const. :
T
•
חוק ) Avogadroפורסם ב" :(1811 -בטמפרטורה זהה ולחץ זהה ,נפחים שווים של גזים
מכילים את אותו מספר של חלקיקים או מולקולות" .במילים אחרות ,בתנאים הנ"ל נפח הגז
נמצא ביחס ישר למספר המולקולות .מתמטית V = const. :או. V ∝ n :
n
חוק הגזים האידיאליים :מכל החוקים החלקיים הנ"ל ,מקבלים את משוואת הגז האידיאלי – "המנה של
מכפלת הלחץ והנפח של גז למכפלת כמותו והטמפרטורה שלו היא קבוע". PV = const. :
nT
הקבוע מכונה קבוע הגזים ומסומן ב ,R -ובעזרתו מקבלים את משוואת הגז האידיאלי בצורתה הידועה:
PV = nRT
לעיתים ,נהוג להשתמש בחוק במונחי הריכוזים. P = CRT :
כמו כן ,ניתן לרשום את המשוואה בצורה מולקולארית ולא מולרית בעזרת קבוע בולצמן:
PV = NkBT
כימיה פיסיקלית א' ) – (69163תרגול מס' (1) :2יחידות (2) ,משוואת הגז האידיאלי (3) ,חוק בר-למבר
11
סמסטר אביב ,תשע"א )(2011
מתרגלים :רועי עשור ואמיר ונד
החוג לכימיה
המכון לכימיה
גודלו של קבוע הגזים R
energy
קבוע הגזים Rנקבע אמפירית ע"י מדידות .יחידותיו:
mol ⋅ K
= ]. [ R
נכון להיום ,גודלו הידוע של הקבוע הוא:
J
= 0.082057 lit ⋅ atm = 1.987 cal
mol ⋅ K
mol ⋅ K
mol ⋅ K
R = 8.314472
תרגיל :חשב את קבוע הגזים בהינתן הידוע לך על נפח של מול גז בתנאי .STP
T = 0 C = 273.15 K 3
.
פיתרון :תנאי : (Standard Temperature and Pressure) STP
P ≅ 1 atm
כידוע לכם מן הקורס הבסיסי בכימיה ,מול של גז בתנאי STPתופס 22.4ליטר. V = V = 22.4 L mol :
n
ולכן ממשוואת הגזים נקבל:
1 ⋅ 22.4 lit mol
R = PV = atm
= 0.082 L ⋅ atm
273.15 K
nT
mol ⋅ K
בהתאמה לערך הניסוני שהובא לעיל.
הנחות המודל ותקפותו
למעשה ,משוואת הגז האידיאלי מדויקת למצב של גז אידיאלי ) (idealאו גז מושלם ) .(perfectגזים אלו
הם מודל תיאורטי בלבד ,שהנחותיו הן:
א.
המולקולות מתוארות כנקודות מסה )חסרות נפח(.
ב.
אין אינטראקציות בין המולקולות )אין כוחות משיכה ודחייה(.
ג.
המולקולות עוברות התנגשויות אלסטיות בלבד )שימור אנרגיה קינטית ושימור התנע הקווי( בינן
לבין עצמן ועם דופן הכלי המכיל אותן.
לכן ,משוואת הגז האידיאלי לעולם אינה תקפה במדויק לגזים אמיתיים ,אך עם זאת במקרים מסוימים היא
מהווה קירוב טוב )ואף מצוין(.
התנאים בהם תקפות המשוואה גבוהה יחסית הם למשל :לחץ נמוך ,אטומים )למשל :גזים אצילים(,
מולקולות נטולות דיפול קבוע וספריות.
למצבים אחרים ,ישנן משוואות עם תיקונים ,כגון משוואת ון-דר-ואלס )בה תיתקלו במסגרת לימודיכם
בקורס "כימיה פיסיקלית ב' :תרמודינמיקה"( בשנה הבאה.
3לפי ההגדרה הנוכחית של ה ,IUPAC -תנאי הלחץ ב STP -הוא ,100 kPaלמרות שבעבר הייתה נהוגה ההגדרה של תנאי
ה STP -כ .1atm=101,325 Pa -לצורך התרגיל ,נשתמש בהגדרה הקודמת לשם נוחות.
כימיה פיסיקלית א' ) – (69163תרגול מס' (1) :2יחידות (2) ,משוואת הגז האידיאלי (3) ,חוק בר-למבר
12
סמסטר אביב ,תשע"א )(2011
מתרגלים :רועי עשור ואמיר ונד
החוג לכימיה
המכון לכימיה
דוגמה )גז אידיאלי +יחידות(:
צמיג מכונית נופח ללחץ 24 PSIביום חורפי כשהטמפרטורה הייתה .-5ºCבהנחה שהנפח קבוע ולא היו
דליפות אוויר מן הצמיג ,מה יהיה הלחץ בצמיג באטמוספירות ביום קיצי בו הטמפרטורה היא ? 35ºC
הערה :היחידה PSIהיא יחידה שימושית ללחץ בצמיגי מכוניות ,ומשמעותה היא Pounds per Square Inch
כאשר.1 Pound=450 gr , 1 Inch = 2.54 cm :
פיתרון:
ראשית ,נשתמש במשוואת הגז האידיאלי. PV = nRT :
נשים לב ,כי במהלך כל השאלה הנפח ) (Vוכמות המולים ) (nנשארים קבועים לפי הנתון .ולכן ,למעשה
צפיפות האוויר בתוך הצמיג קבועה .נכתוב לשם נוחות את המשוואה בצורה. P = CRT :
לכן ,בשאלה מספיק להבין כי היחס בין הלחץ לטמפרטורה הוא לחץ ישר.
נסמן ב P1 , T1 -את התנאים ביום החורפי ,וב P2 , T2 -את התנאים ביום הקיצי .נקבל:
P2 P1
T
=
⇒ P2 = 2 P1
T2 T1
T1
לפי הנתונים:
T2
P = 308 × 24 = 27.58 PSI
T1 1 268
= P2
⇒
P1 = 24 PSI
T1 = −5 C = 268 K
T2 = 35 C = 308 K
כעת ,נותר רק לתרגם את היחידות מ PSI -לאטמוספירה .שימו לב ,כי היחידה PSIאינה יחידת לחץ
"אמיתית" )כוח לשטח( אלא יחידה של מסה לשטח .לכן ,בתרגום צריך גם להפוך את המסה לכוח ,וזאת
בעזרת קבוע הכבידה ,gעל סמך הנוסחה . F = mg :לכן:
2
2
gr −3 kg 1 inch 2 cm
lb
m
lb
1 PSI = 1
=1
× 450
× 10
×
= × 10 m × 9.8 2
inch2
inch 2
lb
gr 2.54 cm
sec
kg m 2
= 6835.51 sec
= 6835.51 N2 = 6835.51 Pa = 0.0675 atm
m2
m
ולכן ,התשובה במקרה שלנו היא:
P2 = 27.58 PSI = 1.861 atm
כימיה פיסיקלית א' ) – (69163תרגול מס' (1) :2יחידות (2) ,משוואת הגז האידיאלי (3) ,חוק בר-למבר
13
סמסטר אביב ,תשע"א )(2011
מתרגלים :רועי עשור ואמיר ונד
החוג לכימיה
המכון לכימיה
חוק דלטון – 1801 - Dalton’s Law of Partial Pressures
החוק עוסק בתערובת של גזים אידיאליים המצויים באותו הכלי.
החוק קובע כי כל גז מפעיל לחץ על הקירות כאילו היה לבדו בכלי ,מבלי קשר לנוכחות שאר הגזים –
כלומר ,הלחץ שהגז מפעיל כשהוא נמצא בתערובת זהה ללחץ שהיה מפעיל לו היה לבדו.
הלחץ שכל גז מפעיל מכונה הלחץ החלקי ) ,(Partial Pressureומתקיים כי הלחץ הכולל של התערובת
שווה לסכום הלחצים החלקיים של כל מרכיבי התערובת בנפרד ,ללא תלות בסוג הגז.
כלומר ,כל אחד מן הגזים מקיים את משוואת הגזים האידיאליים בנפרד.
כעת ,בצורה מעט יותר פורמלית:
•
הלחץ הכולל המופעל ע"י מערכת גזית שווה לסכום הלחצים החלקיים
) (partial pressuresשל כל אחד מן הרכיבים בתערובת הגזים
בנפרד .בצורה מתמטית ,נוכל לרשום את החוק כ:
Ptot = ∑ Pi
)(i - gaseous component
i
בניסוח שונה :אם נתונים לנו Nנפחים שווים המאוכלסים ב N -גזים
שונים בטמפרטורה ,Tכאשר הלחץ בכל נפח הוא ,Piאזי אם נרכז את
כל הגזים יחד באותו נפח Vובאותה טמפרטורה ,Tנקבל את הלחץ
Ptotשהוגדר לעיל )וראו הסכימה מצד שמאל(.
•
החוק מיוחס למשוואת הגז האידיאלי .מניחים כי הגזים לא מגיבים זה
)John Dalton (1766-1844
עם זה .אזי נוכל להסיק את המסקנות הבאות )הנובעות זו מזו(:
oהלחץ החלקי שמפעיל כל מרכיב גזי הוא המכפלה של
שברו המולרי בלחץ הכולל:
ni RT
= χi n RT = Ci RT
V
V
= Pi
Pi = χ i Ptot
⇒
כאשר השבר המולרי הוא החלק היחסי )במולים( של
המרכיב הגזי מכלל התערובת:
where ntot = ∑ ni
i
ni
ntot
= χi
oהיחס בין הלחצים החלקיים של הגזים זהה ליחס בין כמות
הגזים במולים.
.
χi
χj
=
ntot
ni
nj
ntot
Pi ni
= =
Pj n j
כימיה פיסיקלית א' ) – (69163תרגול מס' (1) :2יחידות (2) ,משוואת הגז האידיאלי (3) ,חוק בר-למבר
14
סמסטר אביב ,תשע"א )(2011
מתרגלים :רועי עשור ואמיר ונד
החוג לכימיה
המכון לכימיה
המסקנה החשובה לנו מחוק דלטון היא שנוכל לבצע מעבר ישיר ופשוט מלחצים לריכוזים .כלומר ,אם
נמצא את הלחץ החלקי של גז כתלות בזמן נוכל לתרגמו לריכוז כתלות בזמן.
למשל ,עבור ריאקציה מסדר ראשון אותה פתרנו בפעם שעברה:
PA = PA (0)e − kt
PA PA (0) − kt
=
e
⇒
RT
RT
ideal gas law
→
Ci = Pi / RT
[ A] = [ A]0 e − kt
בקורס אנחנו ניישם את הקשר שבין הגודל המדיד )הלחץ הכולל בכלי( לבין הגדלים המעניינים אותנו
)קצב הריאקציה ,מידת התקדמותה וכו'(:
למשל ,בריאקציה ) N 2O5( g ) → 2 NO2( g ) + 12 O2( gניתן לראות כי מכל 2מולקולות גז שנצרכות
נוצרות 5חדשות ,משמע הלחץ הולך ועולה )היות והוא פרופורציונאלי למס' המולקולות(.
נדגים איך מבצעים את החישוב מתמטית.
בהנחה שנפח כלי התגובה לא משתנה ,העבודה בריכוזים/לחצים או בכמויות )מולים( אקוויולנטית,
וניתן לבחור לעבוד במה שנוח .אנו נבחר לעבוד ישירות בלחצים .למשל ,עבור הריאקציה הנ"ל
נניח כי התחלנו מריכוז [N2O5]0של N2O5בלבד בכלי ,וכי V*xמולקולות הגיבו ,כלומר
הריכוז של המגיב קטן ב .x -לכן ,נוכל מיד לרשום:
) 2 NO2( g ) + 12 O2( g
→
) N 2O5( g
Ctot (0) = [ N 2O5 ]0
0
0
[ N 2O5 ]0
Ctot (t ) = [ N 2O5 ]0 + 1.5 x
0.5 x
2x
[ N 2O5 ]0 − x
t = 0:
:
t
שימו לב שחובה להתייחס למקדמים הסטויכיומטריים !
כעת ,ברור שלפי חוק הגזים האידיאליים בניסוחו P = CRT :נקבל כי:
P(t = 0) = [ N 2 O5 ]0 RT
P(t ) = ([ N 2O5 ]0 + 1.5 x ) RT
ומכאן שבעזרת מדידת הלחץ בלבד ,נוכל לקבוע את ,xכלומר את מידת ההתקדמות של התגובה,
ומכאן גם את קצבה )נוכל לדעת כמה מגיב הגיב בכל זמן נתון(.
הערה :חוק זה לעיתים מתאים גם עבור תערובת של גזים לא אידיאלים בתנאי שאין ביניהם תגובה כימית
וחסרונו הוא שאינו מתאים לנוזלים.
הערה :2כבר עכשיו ברור כי נוכל להשתמש במדידת לחץ ככלי למעקב אחרי קצב ריאקציות רק עבור
ריאקציות שיש בהן מגיב/תוצר גזי )לפחות אחד( ,ורק כאשר מס' מולי הגז משתנה במהלך הריאקציה
)בין המגיבים לתוצרים( – אחרת הלחץ הכולל בכלי )הגודל המדיד( לא ישתנה.
כימיה פיסיקלית א' ) – (69163תרגול מס' (1) :2יחידות (2) ,משוואת הגז האידיאלי (3) ,חוק בר-למבר
15
סמסטר אביב ,תשע"א )(2011
מתרגלים :רועי עשור ואמיר ונד
החוג לכימיה
המכון לכימיה
דוגמה כללית לשימוש בחוק דלטון:
בטמפרטורה קבועה לוקחים 6.2ליטר של חנקן בלחץ של 738torrו 15.2 -ליטר של חמצן בלחץ של
325torrומערבבים את 2הגזים בכלי שנפחו 12ליטרים.
א .מהו הלחץ של התערובת ?
ב .מהו הרכב התערובת בשברים מולים?
פיתרון:
PV
1 1 = PV
א .נחשב את הלחץ החלקי של כל אחד מהמרכיבים .בטמפרטורה קבועה מתקיים2 2 :
)זהו חוק .(Boyleהיות ואנו מניחים את קיומו של חוק דלטון ,זה מתקיים גם עבור כל גז בנפרד
עבור הלחצים החלקיים.
עבור החנקן:
לפני הערבוב – . V1 = 6.2lit; P1 = 738torrאחרי הערבוב – ? = . V2 = 12lit ; P2
V1P1 738torr ⋅ 6.2L
=
= 381.3 torr
V2
12lit
עבור החמצן :בדומה ,נקבל:
= P2
V1 P1 325torr ⋅15.2 L
=
= 411.67torr
V2
12lit
= P2
לקבלת הלחץ הכולל נשתמש בחוק דלטון ונקבל. Ptot = P(O2 ) + P( N 2 ) = 792.97torr :
ב .חישוב השברים המולים:
בהתבסס על חוק דלטון ,ברור כי השבר המולרי של גז נתון שווה ליחס בין הלחץ החלקי של
אותו הגז ליחס הכולל .לכן:
) n(O2
P(O2 ) 411.67torr
=
=
= 0.52
)) (n(O 2 ) + n( N 2
Ptot
792.97torr
= χO
) n( N 2
P( N 2 ) 381.3torr
=
=
= 0.48
)) (n(O 2 ) + n( N 2
Ptot
792.97torr
= χN
2
2
וכמובן שמתקיים עבור תערובת של שני גזים בלבד )זוהי הדרך לבדוק את החישוב שלנו ,או
לחילופין לחסוך את החישוב השני ע"י המרתו בחישוב קל(:
χ N = 1 − χO
2
כימיה פיסיקלית א' ) – (69163תרגול מס' (1) :2יחידות (2) ,משוואת הגז האידיאלי (3) ,חוק בר-למבר
2
16
מתרגלים :רועי עשור ואמיר ונד
חלק ג' – ספקטרופוטומטריה
סמסטר אביב ,תשע"א )(2011
החוג לכימיה
המכון לכימיה
)ראו קובץ עזר נפרד לפירוט נוסף(
ספקטרופוטומטריה )מדידת בליעת אור(
הספקטרוסקופיה היא הענף העוסק ביחסי הגומלין שבין האור והחומר; מדידה ספקטרוסקופית היא
מדידה שבה מקבלים ספקטרום של רמות אנרגיה או של תדרי קרינה אלקטרומגנטית )למשל,
תדרי אור( .אנו נדון כעת במדידות של בליעה בלבד.
ראשית ,נזכיר מהו הספקטרום האלקטרומגנטי )עם הגדלה של אזור האור הנראה(:
לכל חומר ספקטרום בליעה אופייני לו ,שהוא בגדר "טביעת אצבע" של החומר.
השיטה שנסביר להלן ניתנת ליישום במצבי הצבירה גז ונוזל ,במידה ולאחד הצורונים
)מגיבים /תוצרים( הנחקרים יש בליעה אופיינית באורך גל הייחודי לו.
הערות:
• זכרו ,כי בתחום הנראה ,הצבע שאנחנו רואים בעין הוא בדרך
כלל הצבע שאינו מופיע כדומיננטי בספקטרום הבליעה ,אלא
להיפך :התחום שמועבר/מוחזר.
למשל Fe(SCN)2+ ,הוא קומפלקס בצבע אדום – משמע שהוא
בולע בעיקר בירוק.
דרך תיאורית לקשר בין צבע האור הנצפה מעצם לצבע האור
הנבלע בו היא ע"י גלגל צבעים ,כגון זה המוצג בצד שמאל ,שבו
כל צבע מופיע אל מול הצבע המשלים שלו )למשל ,גוף צהוב בולע בסגול ולהיפך(.
• חומר "שקוף" -לא בולע בנראה :רוב הממסים השקופים בולעים ב) UV -מים ,אתאנול וכו'(.
בעמוד הבא נסביר על הטכניקה הניסיונית למדידת בליעה ,ולאחר מכן נשוב לנושא הקשר בין
מדידת בליעה לבין משוואות הקצב ,שהוא נושא התרגול וקורס זה בכלל .
כימיה פיסיקלית א' ) – (69163תרגול מס' (1) :2יחידות (2) ,משוואת הגז האידיאלי (3) ,חוק בר-למבר
17
מתרגלים :רועי עשור ואמיר ונד
סמסטר אביב ,תשע"א )(2011
החוג לכימיה
המכון לכימיה
מדידת בליעה
במעבדה ,מודדים בליעה בעזרת ספקטרופוטומטר ) .(spectrophotometerתרשים סכמטי של
פעולת ספקטרופוטומטר מופיע להלן:
.1
מקור אור )מנורה(.
.2
מונוכרומטור – בורר אורכי גל.
.3
תא הדוגמה הנחקרת.
.4
גלאי )מד עוצמה(.
העוצמה )שמסומנת ב (I -נמדדת בדרך כלל ביחידות של אנרגיה ליח' זמן ,כלומר הספק.
– I0העוצמה של הקרן המגיעה ממקור האור ,לפני המעבר בדגם.
– Iהעוצמה של הקרן לאחר המעבר בדגם.
כאשר אור פוגע בתווך מסוים ,ייתכנו מספר תהליכים שונים:
בליעה – האור נבלע ע"י הדגם .כלומר ,חלק מאנרגית האור נבלעת בחומר ומעוררת
אותו )מוסיפה לו אנרגיה(; בתחום הנראה ,מדובר בד"כ בעירור אלקטרוני )דרגת החופש
האלקטרונית היא שמקבלת את האנרגיה ,באנאלוגיה לאטום מימן שיעורר מאורביטל 1S
לאורביטל ,2Pלמשל(.
החזרה – חלק מן האור יכול להיות מוחזר ,בין אם באופן מסודר )כמו ע"י מראה ,שריג
וכו'( ובין אם בצורה לא מכוונת.
פיזור – חלק מן האור גם עשוי לעבור תהליך של פיזור עקב המעבר בדגם
אנו נתעלם מתהליכי הפיזור וההחזרה לצרכינו ,ונתמקד בתהליך הבליעה.
כימיה פיסיקלית א' ) – (69163תרגול מס' (1) :2יחידות (2) ,משוואת הגז האידיאלי (3) ,חוק בר-למבר
18
מתרגלים :רועי עשור ואמיר ונד
סמסטר אביב ,תשע"א )(2011
החוג לכימיה
המכון לכימיה
הרעיון במדידה הוא השוואה בין הערך של I0לערך של Iעל מנת לקבוע כמה מן האור נבלע
בדגם )ולכן לא מועבר הלאה( .מודדים את הערכים הללו עבור כל אורך גל בנפרד.
נהוג להגדיר שני גדלים חשובים:
א .העברה ) (Transmittanceמוגדרת כ) T = I :גודל חסר יחידות ,מופיע בד"כ באחוזים(.
I0
טווח הערכים האפשרי) 0 ≤ T ≤ 1 :בגדלים( או ) 0 ≤ T ≤ 100באחוזים(.
I
ב .בליעה ) (Absorbanceמוגדרת כA = − log10 T = − log10 I = log10 0 :
I
0
I
)גם כן גודל חסר יחידות(.
טווח הערכים האפשרי. A ≥ 0 :
הערות:
.1
כאשר ,(A=0) T=1כל האור עובר דרך החומר וכלום לא נבלע .משמע ,החומר שקוף
לאורך הגל המוקרן עליו.
.2
Tו A -מוגדרים כך שתמיד יהיו גדלים חיובי .היחס ביניהם לוגריתמי/מעריכי !!!
חוק בר-למבר ) (Beer-Lambert Lawהוא חוק ניסיוני המקשר בין הבליעה של חומר באורך גל
נתון לבין ריכוזו בתמיסה .החוק מתקבל כפיתרון של משוואת מעבר הגל האלקטרומגנטי בתא ,שהיא
משוואה דיפרנציאלית )ראו פיתוח סמי-כמותי בנספח לתרגול זה(.
חוק בר-למבר תקף בתנאים מסוימים )ריכוזים נמוכים של מומס ,עוצמות הארה נמוכות ,מומס עם
כוחות חלשים בין המולקולות וכו'( ,וקיימות ממנו סטיות רציניות מחוץ לתחומים אלו..
החוק מתאר דעיכה אקספוננציאלית של העוצמה לאורך התא. I = I 0 ⋅ exp ( −α lc ) :
ומוכר יותר בצורתו הבאה - A = ε lc :הבליעה ליניארית בריכוז !
כאשר:
–l
אורך התא )בדרך כלל נמדד ב.([cm] -
–c
ריכוז )בדרך כלל נמדד ב.([M] -
–ε
מקדם הבליעה המולרי – ) Molar Absorptivityביחידות של ] .([M cm
-1
-1
מכונה גם מקדם האקסטינקציה ) (Extinctionהמולרי .מתקיים. ε ≡ α :
ln10
מייצג את הסיכוי של אור הפוגע בתווך להיבלע על ידו ,או במילים אחרות מה הנטייה
של החומר לבלוע את האור )קשור לגודל חתך הפעולה לבליעה(.
כימיה פיסיקלית א' ) – (69163תרגול מס' (1) :2יחידות (2) ,משוואת הגז האידיאלי (3) ,חוק בר-למבר
19
מתרגלים :רועי עשור ואמיר ונד
סמסטר אביב ,תשע"א )(2011
זכרו כי εתלוי ,כמובן ,בחומר אך גם באורך הגל .למעשה ,לעתים רושמים את חוק בר-למבר
בצורה , Aλ = ε λ lc :על מנת להזכיר מפורשות את התלות באורך הגל.
לפי חוק בר-למבר ,נוכל להמיר את משוואות הקצב לריכוזים במשוואות קצב לבליעה.
הקשר בין מדידת בליעה למשוואות קצב קינטיות
כמובן ,שנוכל להפעיל את הכלי של הבליעה רק עבור מולקולות הבולעות באורך גל מדיד ניסיונית,
ובדרך כלל מדובר במדידה אופיינית ובולטת השונה משאר הצורונים בריאקציה .למשל:
הריאקציה , N 2O5( g ) → 2 NO2( g ) + 12 O2( g ) :שבה לגז NO2בליעה אופיינית בנראה .
הריאקציה . Cl2( g ) + Br2( g ) → 2 BrCl( g ) :נשים לב כי בריאקציה זו אין שינוי בלחץ ) 2מול גז
יוצרים 2מול גז( ולכן לא נוכל למדוד אותה באמצעי זה ,אך הבליעה משתנה :ל Cl2 -צבע ירוק
אופייני ,ול Br2 -צבע חום-אדום אופייני – השינוי בבליעה בצבעים אלו מעיד על ריכוזי המגיבים
שנותרו.
כימיה פיסיקלית א' ) – (69163תרגול מס' (1) :2יחידות (2) ,משוואת הגז האידיאלי (3) ,חוק בר-למבר
20
החוג לכימיה
המכון לכימיה
סמסטר אביב ,תשע"א )(2011
מתרגלים :רועי עשור ואמיר ונד
החוג לכימיה
המכון לכימיה
נספח )הרחבה( :קבלת חוק בר-למבר משיקולים ראשוניים
כאמור ,על מנת לקבל את בר-למבר בצורה מלאה ,יש לפתור פיתרון מלא של משוואת הגלים ומשוואות
מקסוול בתוך תווך דיאלקטרי.
עם זאת ,נציע כאן פיתרון סמי-כמותי ,הנובע על היגיון פשוט ושיקולים ראשוניים לקבלת החוק .כמו כן,
הפיתרון בוחן את השאלה המאקרוסקופית )ברמת החומר( ולא המיקרוסקופית )ברמת המולקולות(.
נתבונן באלומת אור המתקדמת בכיוון ציר zבתוך
תא המכיל דוגמה בריכוז .c
נתבונן בשכבה דקה ,בעובי .dz
מספר המולקולות בשכבה זו פרופורציונאלי ל.cdz -
נייחס למולקולות מסוג מסוים מקדם בליעה ,שנסמנו
לעת עתה ב . α -משמעות מקדם זה ברמת ההסבר
שכאן היא הסתברותית :הסיכוי שמולקולה תבלע
אור באורך גל נתון.
אזי ,נוכל להניח כי השינוי בעוצמת ההארה עקב המעבר דרך השכבה הדקה פרופורציונאלי למספר
המולקולות ,למקדם הבליעה שלהן ולעוצמה המקורית .בכתיב דיפרנציאלי:
dI
= −α cdz
I
or
) dI ( z ) = −ε cdzI ( z
אינטגרציה על משוואה זו )שימו לב כי היא כתובה בהפרדת משתנים( תיתן:
ln I = −α cz + const.
אם נסמן את עוצמת האור הנכנס לדוגמה ב ,I0 -אזי נקבל את תנאי השפה. I ( z = 0) = I 0 :
הצבתו בפיתרון הכללי הנ"ל תיתן את הפיתרון:
I ( z ) = I 0 e−α cz
ובפרט אם הדוגמה שלנו בעובי ) lהדרך האופטית היא (lנקבל את חוק בר-למבר:
I = I 0 e−α lc
כאשר ,נהוג להציג את החוק בצורתו המוכרת יותר ע"י לקיחת logמשני הצדדים:
) ln ( e
I
= ) A = log10 0 = log10 ( eα lc
= α lc ≡ ε lc
I
ln10
ln10
α lc
כאשר בשורה האחרונה הגדרנו את מקדם הבליעה המולרי ) ( εע"י. ε ≡ α :
ln10
כימיה פיסיקלית א' ) – (69163תרגול מס' (1) :2יחידות (2) ,משוואת הגז האידיאלי (3) ,חוק בר-למבר
21