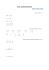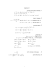אונ` בן – סה דנ מכינה לה – מתמטיקה גוריון

Transcription

‫מתמטיקה – מכינה להנדסה – אונ' בן‬
‫גוריון‬
‫‪1‬‬
‫תלמידים יקרים‬
‫ספר תרגילים זה הוא פרי שנות ניסיון רבות של המחבר בהגשה לבחינות‬
‫הבגרות במתמטיקה הן בבתי הספר התיכוניים‪ ,‬הן בבתי הספר‬
‫הפרטיים והן במכינות האוניברסיטאיות‪.‬‬
‫שאלות תלמידים וטעויות נפוצות וחוזרות הולידו את הרצון להאיר את‬
‫הדרך הנכונה לעומדים בפני מקצוע חשוב זה‪.‬‬
‫הספר מסודר לפי נושאים ומכיל את כל חומר הלימוד על פי תכנית‬
‫הלימודים של משרד החינוך‪ .‬הניסיון מלמד כי לתרגּול בקורס זה‬
‫חשיבות יוצאת דופן‪ ,‬ולכן ספר זה בולט בהיקפו ובמגוון התרגילים‬
‫המופיעים בו‪.‬‬
‫לכל התרגילים בספר פתרונות מלאים באתר ‪www.bagrut.co.il‬‬
‫הפתרונות מוגשים בסרטוני וידאו המלווים בהסבר קולי‪ ,‬כך שאתם‬
‫רואים את התהליכים בצורה מובנית‪ ,‬שיטתית ופשוטה‪ ,‬ממש כפי‬
‫שנעשה בשיעור פרטי‪ .‬הפתרון המלא של השאלה מכוון ומוביל לדרך‬
‫חשיבה נכונה בפתרון בעיות דומות מסוג זה‪.‬‬
‫תקוותי היא שספר זה ישמש מורה‪-‬דרך לכם התלמידים ויוביל אתכם‬
‫להצלחה‪.‬‬
‫יוחאי טוויג‬
‫‪© www.bagrut.co.il‬‬
‫‪2‬‬
‫תוכן העניינים‬
‫פרק ‪ – 1‬מבוא לאלגברה‪5 ......................................................................................... :‬‬
‫פרק ‪ – 2‬טכניקה אלגברית‪21 .................................................................................... :‬‬
‫פירוק הטרינום‪21 ............................................................................................................... :‬‬
‫משוואות‪22 ........................................................................................................................ :‬‬
‫משוואה ממעלה ראשונה‪22 ............................................................................................. :‬‬
‫מערכת שתי משוואות בשני נעלמים ממעלה ראשונה‪23 ..................................................... :‬‬
‫משוואות עם אינסוף פתרונות וללא פתרון‪25 .................................................................... :‬‬
‫משוואה ממעלה שנייה‪25 ................................................................................................ :‬‬
‫משוואות ממעלה שלישית ומשוואות דו‪-‬ריבועיות‪26 ......................................................... :‬‬
‫משוואות עם פרמטרים‪26 ................................................................................................ :‬‬
‫משוואות עם שורשים‪27 .................................................................................................. :‬‬
‫משוואות עם ערך מוחלט‪27 ............................................................................................. :‬‬
‫מערכת משוואות ממעלה שנייה‪29 ....................................................................................:‬‬
‫תשובות סופיות‪29 ........................................................................................................... :‬‬
‫אי שוויוניים‪32 ................................................................................................................... :‬‬
‫אי‪-‬שוויונים ממעלה ראשונה‪32 ........................................................................................ :‬‬
‫אי‪-‬שוויונים ממעלה שנייה‪32 ........................................................................................... :‬‬
‫אי‪-‬שוויונים ממעלה שלישית‪34 ........................................................................................ :‬‬
‫אי‪-‬שוויונים עם מנה‪34 .................................................................................................... :‬‬
‫אי‪-‬שוויונים כפולים ‪ -‬מערכת וגם‪34 ................................................................................. :‬‬
‫שאלות מסכמות – אי ‪-‬שוויונים‪36 .................................................................................... :‬‬
‫תשובות סופיות‪36 ........................................................................................................... :‬‬
‫תחום הגדרה‪37 ............................................................................................................... :‬‬
‫תשובות סופיות‪37 ........................................................................................................... :‬‬
‫פרק ‪ – 3‬חוקי חזקות ומשוואות מעריכיות ולוגריתמיות‪39 ................................................ :‬‬
‫חוקי חזקות‪39 .................................................................................................................... :‬‬
‫שאלות יסודיות – חוקי חזקות ושורשים‪39 ...................................................................... :‬‬
‫משוואות מעריכיות‪40 ......................................................................................................... :‬‬
‫שאלות יסודיות – משוואות מעריכיות‪40 .......................................................................... :‬‬
‫משוואות לוגריתמיות‪41 ...................................................................................................... :‬‬
‫שאלות יסודיות – חוקי הלוגריתמים ומשוואות לוגריתמיות‪42 .......................................... :‬‬
‫אי שוויונים מעריכיים‪45 ..................................................................................................... :‬‬
‫‪3‬‬
‫אי‪-‬שוויונים לוגריתמיים‪45 ..................................................................................................:‬‬
‫תירגול נוסף‪46 .................................................................................................................... :‬‬
‫חזרה על חוקי חזקות ושורשים‪46 .................................................................................... :‬‬
‫תשובות סופיות‪48 ........................................................................................................... :‬‬
‫משוואות מעריכיות‪49 ..................................................................................................... :‬‬
‫תשובות סופיות‪52 ........................................................................................................... :‬‬
‫הגדרת הלוגריתם ומשוואות לוגריתמיות יסודיות‪53 ......................................................... :‬‬
‫תשובות סופיות‪57 ........................................................................................................... :‬‬
‫חוקי הלוגריתמים ומשוואות לוגריתמיות‪58 ..................................................................... :‬‬
‫תשובות סופיות‪62 ........................................................................................................... :‬‬
‫מעבר מבסיס לבסיס ומשוואות לוגריתמיות‪63 ................................................................. :‬‬
‫תשובות סופיות ‪65 .......................................................................................................... :‬‬
‫אי‪-‬שוויוניים לוגריתמיים‪66 ............................................................................................ :‬‬
‫תשובות סופיות‪66 ........................................................................................................... :‬‬
‫פרק ‪ – 4‬גאומטריה אוקלידית‪67 ................................................................................:‬‬
‫רקע‪ ,‬קווים וזוויות‪ ,‬משולשים‪67 ......................................................................................... :‬‬
‫משולש כללי‪ ,‬משולש שווה שוקיים‪ ,‬משולש ישר זווית‪67 ...................................................... :‬‬
‫חפיפת משולשים‪69 ............................................................................................................. :‬‬
‫זווית חיצונית למשולש ומשולש ישר זווית‪70 ........................................................................ :‬‬
‫קטעים מיוחדים במשולש‪72 ................................................................................................ :‬‬
‫מרובעים‪73 ......................................................................................................................... :‬‬
‫המעגל‪81 ............................................................................................................................ :‬‬
‫פרופורציה דמיון‪88 ............................................................................................................. :‬‬
‫שאלות שונות‪104................................................................................................................. :‬‬
‫שאלות ללא פרופורציה‪104............................................................................................... :‬‬
‫שאלות הכוללות פרופורציה ודמיון‪107.............................................................................. :‬‬
‫תשובות סופיות‪117.......................................................................................................... :‬‬
‫פרק ‪ – 5‬טריגונומטריה במישור‪118 ............................................................................ :‬‬
‫משולש ישר זווית‪118........................................................................................................... :‬‬
‫זהויות טריגונומטריות‪122................................................................................................... :‬‬
‫משוואות טריגונומטריות‪125................................................................................................ :‬‬
‫טריגונומטריה במישור‪130................................................................................................... :‬‬
‫‪4‬‬
‫פרק ‪ – 1‬מבוא לאלגברה‪:‬‬
‫בסרטון זה הסבר על פעולות חשבון במספרים‬
‫‪ )1‬סמנו את המספרים הבאים על ציר המספרים בהתאמה‪:‬‬
‫‪1‬‬
‫‪1‬‬
‫‪1‬‬
‫‪1‬‬
‫‪1‬‬
‫‪1 1‬‬
‫‪,  , 3 , 3 , 1 , 2 ,‬‬
‫‪, 1 , 2‬‬
‫‪2‬‬
‫‪2‬‬
‫‪2‬‬
‫‪2‬‬
‫‪2‬‬
‫‪2 2‬‬
‫‪1‬‬
‫חשב את ערכי הביטויים הבאים‪:‬‬
‫‪)2‬‬
‫‪6 1‬‬
‫‪)3‬‬
‫‪6 1‬‬
‫‪)4‬‬
‫‪6  1‬‬
‫‪)5‬‬
‫‪6  1‬‬
‫‪)6‬‬
‫‪5  13  9‬‬
‫‪)7‬‬
‫‪5  7  23  1‬‬
‫‪)8‬‬
‫‪5  8 12  17‬‬
‫בסרטון זה הסבר על כפל וחילוק במספרים מכוונים‬
‫‪)9‬‬
‫‪2   5 )11‬‬
‫‪25‬‬
‫‪2  5 )11‬‬
‫‪2   5 )12‬‬
‫‪ 2   3   4 )13‬‬
‫‪ 2  3   4 )14‬‬
‫‪8 : 4 )15‬‬
‫‪50 : 10 )16‬‬
‫‪15 : 3 )17‬‬
‫‪6 : 2 )18‬‬
‫‪ 25 :  5 )19‬‬
‫‪ 30 : 3 )21‬‬
‫‪5‬‬
‫‪7   2  )21‬‬
‫‪)22‬‬
‫‪32‬‬
‫‪4‬‬
‫‪)23‬‬
‫‪12‬‬
‫‪3‬‬
‫‪0 : 5 )24‬‬
‫‪ 2   0 )25‬‬
‫בסרטון זה הסבר על חזקה ושורש‬
‫‪)26‬‬
‫‪)27‬‬
‫‪24‬‬
‫‪ 2  )29‬‬
‫‪4‬‬
‫‪23 )28‬‬
‫‪)31‬‬
‫‪3‬‬
‫‪26‬‬
‫‪ 2 ‬‬
‫‪24 )31‬‬
‫‪ 2 ‬‬
‫‪)32‬‬
‫‪23‬‬
‫‪)33‬‬
‫‪4‬‬
‫‪)34‬‬
‫‪64‬‬
‫‪)35‬‬
‫‪64‬‬
‫‪32 )36‬‬
‫‪5‬‬
‫‪)37‬‬
‫‪16‬‬
‫‪)38‬‬
‫‪64‬‬
‫‪4‬‬
‫‪)39‬‬
‫‪64‬‬
‫‪)41‬‬
‫‪64‬‬
‫‪)41‬‬
‫‪34  3 8‬‬
‫‪3‬‬
‫‪3‬‬
‫‪4‬‬
‫‪42 )43‬‬
‫‪)42‬‬
‫‪169‬‬
‫‪)44‬‬
‫‪2‬‬
‫‪ 4 ‬‬
‫‪)45‬‬
‫‪3‬‬
‫‪ 3‬‬
‫‪)46‬‬
‫‪27‬‬
‫‪3‬‬
‫‪625 )47‬‬
‫‪4‬‬
‫‪)48‬‬
‫‪16‬‬
‫‪4‬‬
‫‪32‬‬
‫‪5‬‬
‫‪)51‬‬
‫‪2‬‬
‫‪)49‬‬
‫‪  5‬‬
‫בסרטון זה הסבר על סדר פעולות חשבון‬
‫‪196  5  22  20 : 2 )51‬‬
‫‪)53‬‬
‫‪)52‬‬
‫‪: 2  10   2 ‬‬
‫‪3‬‬
‫‪4‬‬
‫‪ 2‬‬
‫‪64 :  4  2   42   32  10  )54‬‬
‫‪32  4 5  4   7  2   900‬‬
‫‪6‬‬
7
‫‪)55‬‬
‫‪2‬‬
‫‪144  20 : 4  3   2 ‬‬
‫‪)56‬‬
‫‪3  4  3  4   2   10  6‬‬
‫‪4‬‬
‫‪3‬‬
‫‪ 3 :  9  5   2 )57‬‬
‫‪ 9  52 :  4  1  24 :12  3 )58‬‬
‫‪25 :  8  42  3  5 )59‬‬
‫‪27  4  32  2  33 )61‬‬
‫‪6   14  10   13    15 )61‬‬
‫‪‬‬
‫‪‬‬
‫‪ 2  15  20 :  4  3  2  )63‬‬
‫‪3‬‬
‫‪)62‬‬
‫‪‬‬
‫‪3‬‬
‫‪‬‬
‫‪64  2   4   5 243‬‬
‫‪3‬‬
‫‪8 ‬‬
‫‪32   8  2  3‬‬
‫‪ 3  72    4 ‬‬
‫‪5‬‬
‫‪2‬‬
‫בסרטון זה הסבר על שברים‬
‫המירו את השברים המדומים לשברים מעורבים‪:‬‬
‫‪)64‬‬
‫‪3‬‬
‫‪2‬‬
‫‪)65‬‬
‫‪8‬‬
‫‪5‬‬
‫המירו את השברים המעורבים לשברים מדומים‪:‬‬
‫‪3‬‬
‫‪)66‬‬
‫‪8‬‬
‫‪)67‬‬
‫‪2‬‬
‫‪2‬‬
‫‪5‬‬
‫‪12‬‬
‫איזה שבר גדול יותר?‬
‫‪)68‬‬
‫‪3‬‬
‫‪5‬‬
‫או‬
‫‪7‬‬
‫‪7‬‬
‫‪)69‬‬
‫‪3‬‬
‫‪3‬‬
‫או‬
‫‪5‬‬
‫‪7‬‬
‫‪)71‬‬
‫‪3‬‬
‫‪4‬‬
‫או‬
‫‪4‬‬
‫‪5‬‬
‫המירו את השברים העשרוניים לשברים פשוטים‪:‬‬
‫‪0.3 )71‬‬
‫‪0.02 )72‬‬
‫‪1.012 )73‬‬
‫‪2.75 )74‬‬
‫המירו את השברים הפשוטים לשברים עשרוניים‪:‬‬
‫‪)75‬‬
‫‪1‬‬
‫‪10‬‬
‫‪)79‬‬
‫‪12‬‬
‫‪1000‬‬
‫‪1‬‬
‫‪)76‬‬
‫‪1‬‬
‫‪100‬‬
‫‪)77‬‬
‫‪3‬‬
‫‪1000‬‬
‫‪)78‬‬
‫‪12‬‬
‫‪1000‬‬
‫‪)81‬‬
‫‪3‬‬
‫‪50‬‬
‫‪)81‬‬
‫‪7‬‬
‫‪20‬‬
‫‪)82‬‬
‫‪5‬‬
‫‪6‬‬
‫‪8‬‬
9
‫המירו את האחוזים לשברים פשוטים‪:‬‬
‫‪25% )84‬‬
‫‪50% )83‬‬
‫המירו את השברים הפשוטים לאחוזים‪:‬‬
‫‪)85‬‬
‫‪4‬‬
‫‪10‬‬
‫‪)86‬‬
‫‪5‬‬
‫‪20‬‬
‫המירו את השברים המדומים לשברים מעורבים‪:‬‬
‫‪)87‬‬
‫‪20‬‬
‫‪3‬‬
‫‪‬‬
‫‪)88‬‬
‫‪19‬‬
‫‪4‬‬
‫איזה שבר גדול יותר?‬
‫‪)89‬‬
‫‪)91‬‬
‫‪4‬‬
‫‪3‬‬
‫או‬
‫‪10‬‬
‫‪10‬‬
‫‪5‬‬
‫‪2‬‬
‫או‬
‫‪6‬‬
‫‪3‬‬
‫‪)91‬‬
‫‪)92‬‬
‫‪7‬‬
‫‪7‬‬
‫או‬
‫‪6‬‬
‫‪8‬‬
‫‪7‬‬
‫‪5‬‬
‫או‬
‫‪12‬‬
‫‪18‬‬
‫בסרטון זה הסבר על חיבור וחיסור שברים‬
‫‪)93‬‬
‫‪1 3‬‬
‫‪‬‬
‫‪4 4‬‬
‫‪)94‬‬
‫‪5 7‬‬
‫‪‬‬
‫‪2 4‬‬
‫‪)95‬‬
‫‪3 1 5‬‬
‫‪ ‬‬
‫‪2 4 8‬‬
‫‪)96‬‬
‫‪2 5 1‬‬
‫‪ ‬‬
‫‪3 9 6‬‬
‫‪)97‬‬
‫‪3 5 7‬‬
‫‪ ‬‬
‫‪4 6 5‬‬
‫‪)98‬‬
‫‪1 11‬‬
‫‪1 ‬‬
‫‪8 12‬‬
‫‪)99‬‬
‫‪1 23‬‬
‫‪1  2‬‬
‫‪9 27‬‬
‫‪2 3‬‬
‫‪  3 )111‬‬
‫‪21 14‬‬
‫‪10‬‬
‫‪1‬‬
‫‪)111‬‬
‫‪)113‬‬
‫‪)115‬‬
‫‪)117‬‬
‫‪2 5 6‬‬
‫‪ ‬‬
‫‪8 8 8‬‬
‫‪5 7 2‬‬
‫‪ ‬‬
‫‪4 2 8‬‬
‫‪3 1 8‬‬
‫‪1 ‬‬
‫‪4 5 20‬‬
‫‪7‬‬
‫‪1‬‬
‫‪5 6‬‬
‫‪8‬‬
‫‪2‬‬
‫‪)112‬‬
‫‪)114‬‬
‫‪)116‬‬
‫‪1 4‬‬
‫‪‬‬
‫‪2 3‬‬
‫‪5 1‬‬
‫‪2 ‬‬
‫‪6 9‬‬
‫‪2‬‬
‫‪1‬‬
‫‪3 4‬‬
‫‪3‬‬
‫‪4‬‬
‫בסרטון זה הסבר על כפל וחילוק שברים‬
‫‪)118‬‬
‫‪)111‬‬
‫‪)112‬‬
‫‪)114‬‬
‫‪)116‬‬
‫‪)118‬‬
‫‪2 2‬‬
‫‪‬‬
‫‪3 5‬‬
‫‪1 1‬‬
‫‪2 1‬‬
‫‪3 4‬‬
‫‪2 5‬‬
‫‪:‬‬
‫‪3 6‬‬
‫‪3‬‬
‫‪6:‬‬
‫‪4‬‬
‫‪5 1‬‬
‫‪:3‬‬
‫‪9 3‬‬
‫‪33‬‬
‫‪4‬‬
‫‪)119‬‬
‫‪)111‬‬
‫‪)113‬‬
‫‪)115‬‬
‫‪2‬‬
‫‪5‬‬
‫‪1 2‬‬
‫‪3 2‬‬
‫‪3 5‬‬
‫‪2‬‬
‫‪:4‬‬
‫‪5‬‬
‫‪2 1‬‬
‫‪2 :1‬‬
‫‪3 5‬‬
‫‪4‬‬
‫‪3‬‬
‫‪)117‬‬
‫‪)119‬‬
‫‪3‬‬
‫‪ ‬‬
‫‪4‬‬
‫‪9 1 1 1‬‬
‫‪1  1 :‬‬
‫‪20 3 4 2‬‬
‫‪)121‬‬
‫‪)122‬‬
‫‪)124‬‬
‫‪)126‬‬
‫‪4 2‬‬
‫‪‬‬
‫‪3 7‬‬
‫‪6 2 9‬‬
‫‪ ‬‬
‫‪5 3 4‬‬
‫‪5‬‬
‫‪:3‬‬
‫‪6‬‬
‫‪3 12‬‬
‫‪8 :‬‬
‫‪2 20‬‬
‫‪)121‬‬
‫‪)123‬‬
‫‪)125‬‬
‫‪11‬‬
‫‪1 1‬‬
‫‪5 :‬‬
‫‪3 6‬‬
‫‪1 2‬‬
‫‪3 4‬‬
‫‪2 5‬‬
‫‪3 5‬‬
‫‪3 :5‬‬
‫‪4 8‬‬
12
‫בסרטון זה הסבר על הצבה בתבנית מספר‬
:‫חשב את ערכי הביטויים הבאים‬
a  3a  a  7 , a  1
5
4
3
 x  y
)128
3
, x  5 y  4
)127
1
1
n
2
3
)129
16m2  9n2 , m 
:‫הצב את הערכים המספריים במקום הפרמטרים וחשב את ערך תבנית המספר‬
 a  2c 
a
 x  3
2
4a 2  3b
c
4
2
a  2, c  2
)131
 3 x 2b
x  5, b  1
)133
a
a  1, b  2, c  4
a 2  2ab  b2
 x3  2 xy  y 4
)131
a  3, b  5
)132
x  2, y  1
)134
‫בסרטון זה הסבר על כינוס איברים‬
:‫כנס איברים דומים‬
a5  a5
)136
5x  3x 12 x
)135
1  b2  2b  3  2b2
)138
7m  11  9m  2
)137
x2 y  xy  3 y 2 x  9 xy  5xy 2
)141
4ab  3a2b  3b2 a  5ab
)139


10m2 n  3mn2  m2 n  2m 5
5a2b  8ab2  20a2b  14ab2
)143
13
)141
:‫כנס איברים דומים‬
8a2  10a  5a 2 11a  a 2 )142
‫בסרטון זה הסבר על פתיחת סוגריים‬
:‫פשט את הביטויים הבאים ע"י פתיחת סוגריים‬
x  x  5 )145
2  x  4  )144
2  b  2 x 
)147
7  a  3
)146
2
6x  3 y 
3
)149
x  x 2  3x  2 
)148
 3x  2 y  5 )151
 5 y  7
)151
3x  2 x  y 
)152
x  5  2 x  1
)153
 x  3 5  x  )155
 x  4 x  5 )154
 2 x  5 2 x  5 )157
a  a  2b  c 
)159
3  x  1 x  3
)156
4  3x  2    2 x  1 3x  5
)158
‫בסרטון זה הסבר על נוסחאות כפל מקוצר‬
:‫פשט את הביטויים הבאים באמצעות נוסחאות הכפל המקוצר‬
2
2
 x  2  )161
 a  3 )161
1

c  
4

 5 y  4t 
2
2
)163
 b  1
)165
 2m  5 
 x y  11
2
2
)162
2
)164
2
)166
:‫פשט את הביטויים הבאים באמצעות נוסחאות הכפל המקוצר‬
2
2
 x  4  )167
 5  x  )168
 2m  4c 
2
)171
 9  x  9  x  )172
 4 x  2
2
)169
 x  7  x  7  )171
 3x  4 3x  4 )173
14
15
‫בסרטון זה הסבר על פירוק לגורמים‬
‫פשט את הביטויים הבאים ע"י הוצאת גורם משותף‪:‬‬
‫‪)174‬‬
‫‪2x  4‬‬
‫‪)175‬‬
‫‪3x  6‬‬
‫‪)176‬‬
‫‪80  4x‬‬
‫‪)177‬‬
‫‪64  8a‬‬
‫‪)178‬‬
‫‪x 2  3x‬‬
‫‪)179‬‬
‫‪x3  x‬‬
‫‪)181‬‬
‫‪x5  2 x 2‬‬
‫‪)181‬‬
‫‪4 x3  12 x2‬‬
‫בסרטון זה הסבר על פירוק לפי נוסחאות‬
‫פשט את הביטויים הבאים ע"י הוצאת גורם משותף ושימוש בנוסחאות הכפל‬
‫המקוצר‪:‬‬
‫‪)182‬‬
‫‪x2  6 x  9‬‬
‫‪)183‬‬
‫‪9a 2  12a  4‬‬
‫‪)184‬‬
‫‪12 x2  60 x  75‬‬
‫‪)185‬‬
‫‪x2  16 x  64‬‬
‫‪)186‬‬
‫‪a 2  10a  25‬‬
‫‪)187‬‬
‫‪2 x2  36 x  162‬‬
‫‪)188‬‬
‫‪a2  9‬‬
‫‪)189‬‬
‫‪x 2  16‬‬
‫‪)191‬‬
‫‪81  x 2‬‬
‫‪)191‬‬
‫‪100 x2  49‬‬
‫‪)192‬‬
‫‪49x  x3‬‬
‫‪)193‬‬
‫‪x3  x‬‬
‫‪)194‬‬
‫‪x2  10 x  25‬‬
‫‪)195‬‬
‫‪m2  9‬‬
‫בעיות יסודיות באחוזים‬
‫‪ )196‬בכיתה ‪ 30‬תלמידים‪ 60% .‬מתוכם בנות‪.‬‬
‫א‪ .‬כמה בנות בכיתה?‬
‫ב‪ .‬כמה בנים בכיתה?‬
‫‪ )197‬בכיתה ‪ 28‬בנות המהוות ‪ 70%‬מכלל התלמידים בכיתה‪.‬‬
‫א‪ .‬כמה תלמידים בכיתה?‬
‫ב‪ .‬כמה בנים בכיתה?‬
‫‪ )198‬מחיר בגד ‪-‬ים הוא ‪ .₪ 300‬בסוף העונה הוא נמכר ב ‪ 20%-‬הנחה‪.‬‬
‫א‪ .‬מהו מחירו בסוף העונה?‬
‫‪16‬‬
‫ב‪ .‬מה גודל ההנחה?‬
‫‪ )199‬מחיר ההשקה של בושם מסוים הוא ‪ .₪ 500‬לאחר מכן מועלה מחירו ב‪.8%-‬‬
‫א‪ .‬מה מחירו הסופי?‬
‫ב‪ .‬מה גודל ההתייקרות?‬
‫‪ )211‬מחיר ליטר דלק הוא ‪ ₪ 5‬לליטר‪ .‬בחנוכה מוגל מחירו ב‪.7%-‬‬
‫בפסח מועלה מחירו ב ‪ .7%-‬מה מחירו בסוף השנה?‬
‫‪ )211‬מוצר מסויים מתייקר בסוכות ב ‪ .12%-‬בפורים מוזל המוצר ב ‪.12%-‬‬
‫מחירו בסוף השנה הוא ‪ .₪ 394.24‬מה מחירו בתחילת השנה?‬
‫‪ )212‬באולם קולנוע ‪ 200‬צופים‪ ,‬מתוכם ‪ 176‬בנים‪ .‬מה אחוז הבנים בקהל?‬
‫‪ )213‬בכיתה ‪ 30‬תלמידים‪ ,‬מתוכם ‪ 18‬בנות‪ .‬מה אחוז הבנות בכיתה?‬
‫‪ )214‬מחיר מוצר התייקר מ‪ ₪ 80-‬ל‪ .₪ 120-‬בכמה אחוזים התייקר המוצר?‬
‫‪ )215‬מחיר מוצר הוזל מ‪ ₪ 120-‬ל‪ .₪ 80-‬בכמה אחוזים הוזל המוצר?‬
‫‪ )216‬מחיר מוצר התייקר מ‪ ₪ 150-‬ל‪ .₪ 200-‬בכמה אחוזים התייקר המוצר?‬
‫‪ )217‬מחיר מוזל הוזל מ ‪ ₪ 200-‬ל ‪ .₪ 150-‬בכמה אחוזים הוזל המוצר?‬
‫‪17‬‬
:‫פתרונות‬
)1
.10 )11 .10 )9 .2 )8 .10 )7 .9 )6 . 5 )5 . 7 )4 . 5 )3 . 7 )2
.3 )18 .5 )17 .5 )16 .2 )15 . 24 )14 . 24 )13 . 10 )12 . 10 )11
.64 )27 .16 )26 .0 )25 .0 )24 . 4 )23 . 8 )22 .14 )21 . 10 )21 . 5 )19
.2 )36 .4 )35 .8 )34 .16 )33 .8 )32 . 16 )31 . 8 )31 .16 )29 . 8 )28
.16 )44 . 16 )43 .13 )42 . 83 )41 . 4 )41 .‫) בח"מ‬39 . 2.8 )38 .‫) בח"מ‬37
.88 )52 . 24 )51 .25 )51 . 2 )49 .‫) בח"מ‬48 .5 )47 . 3 )46 . 27 )45
.21 )61 .5 )59 .14 )58 .31 )57 . 37 )56 .19 )55 . 20 )54 . 79 )53
5
62
19
3
1
)68 . )67 . )66 .1 )65 .1 )64 . 20 )63 . 44 )62 . 16 )61
7
8
5
5
2
3
3
1
3
4
3
. 0.01 )76 . 0.1 )75 . 2 )74 .1
)73 .
)72 . )71 . )71 . )69
4
250
10
5
5
50
1
. )83 . 0.833 )82 . 0.35 )81 . 0.06 )81 .1.012 )79 . 0.012 )78 . 0.003 )77
2
5
7
4
3
2
1
. )91 . )91 . )89 . 4 )88 . 6 )87 . 25% )86 . 40% )85 . )84
6
6
10
4
3
4
1
13
5
5
7
7
. 2 )99 .1 )98 . 
)97 . 2 )96 . 5 )95 .1 )94 .1 )93 . )92
20
8
12
18
6
27
11
5
13
5
19
1
5
. 7 )116 . 2
)115 . )114 .
)113 .1 )112 .1 )111 . 2 )111
15
24
16
12
42
18
42
1
4
11
3
4
5
.8 )114 . )113 . )112 .8 )111 . 2 )111 .1 )119 . )118 .  )117
10
5
5
15
8
12
8
1
3
27
1
2
. 32 )121 . )121 . 3 )119 . 6 )118 .
)117 . )116 . 2 )115
10
4
64
6
9
21
2
5
2
4
3 )129 . 4 )128 .1 )127 . 20 )126 . )125 .
)124 .15 )123 .1 )122
3
18
5
5
1
. 4a 2  a )135 . 5 )134 . 71 )133 . 4 )132 . 644 )131 . )131
2
.
. 4x )138 . 2x )137 . 25a2b  22ab2 )136
ab  3a 2b  3b2a )142 b2  2b  2 )141 2m  9 )141 2a5 )139
. 7a  21 )146 . x2  5x )145 15m2 n  3mn2 10m )144 2 y 2 x  8xy  x2 y )143
.15x  10 y )151 . 5 y  7 )151 . 4 x  2 y )149 . x3  3x2 )148 . 2b  4 x )147
.  x2  2 x  15 )155 . x2  9 x  20 )154 .11x  5 )153 . 6 x2  3xy )152
18
. a2  2ab  ac )159 . 6 x2  5x  3 )158 . 4 x2  25 )57 . 3x2 12 x  9 )156
. x2  4 x  4 )163 .16 x2 16 x  4 )162 . 25  10x  x2 )161 . x2  8x  16 )161
4m2  20m  25 )167 c 2 
c 1

)166 b2  2b  1 )165 a2  6a  9 )164
2 16
. 4m2 16mc  16c2 )171 x4 y 2  22 x2 y  121 )169 25 y 2  40 yt  16t 2 )168
. 3  x  2  )175 . 2  x  2  )174 . 9 x2  16 )173 . 81  x2 )172 . x2  49 )171
. x 2  x3  2  )181 . x  x 2  1 )179 . x  x  3 )178 . 8 8  a  )177 . 4  20  x  )176
.  x  8 )185 . 3  2 x  5 )184 .  3a  2  )183 .  x  3 )182 . 4 x2  x  3 )181
2
2
2
2
.  x  4  x  4 )189 .  a  3 a  3 )188 . 2  x  9  )187 .  a  5 )186
2
2
. x  7  x  7  x  )192 . 10 x  7 10 x  7  )191 .  9  x  9  x  )191
.12 .‫ ב‬.18 .‫) א‬196 .  m  3 m  3 )195 .  x  5 )194 . x  x 2  1 )193
.4.9755 )211 .40 .‫ ב‬.540 .‫) א‬199 .60 .‫ ב‬.240 .‫) א‬198 .12 .‫ ב‬.40 .‫) א‬197
2
.33.33% )216 .33.33% )215 .50% )214 .60% )213 .88% )212 .400 )211
.25% )217
19
20
:‫ – טכניקה אלגברית‬2 ‫פרק‬
:‫פירוק הטרינום‬
:‫פרק את הביטויים הבאים לפי פירוק טרינום‬
2 x2  7 x  15
)2
4 x2  8x  3
)1
6 x2  5x  1
)4
3x2  11x  6
)3
x2  5x  4
)6
2 x2  x  6
)5
x2  33x  62
)8
x2  8x  15
)7
:‫פרק את הביטויים הבאים‬
4 x2  8x  3
)9
6 x2  5x  1 )11
x2  5x  4 )11
:‫תשובות סופיות‬
 3x  2 x  3 )3  2 x  3 x  5 )2  2 x  1 2 x  3 )1
 x  1 x  4 )6  x  2 2 x  3 )5  3x  1 2 x  1 )4
 2 x  1 2 x  3 )9  x  2 x  31 )8
 x  3 x  5 )7
.  x  1 x  4 )11  3x  1 2 x  1 )11
21
:‫משוואות‬
:‫משוואה ממעלה ראשונה‬
2 x  x  24
7  2x  7
.‫ג‬
:‫) פתור את המשוואות הבאות‬1
.‫ב‬
6 x  2  8 .‫א‬
7 x  5  2 x  4 x 13
.‫ה‬
2x  6  8  x
.‫ד‬
2  5x  7  3x  8
.‫ז‬
6 x  3  5  7 x  x  5x  7
.‫ו‬
7 x  4 3  4x    x
.‫ב‬
3  x  1  4  2
.‫א‬
5x   3x  7  4  21
.‫ד‬
6  4  x    6  x   3x
.‫ג‬
.‫ו‬
x  x  5  x 2  7 x  8
.‫ה‬
 7  x 1  x    x  3
2
0
4 x 3x

1
15 10
5 x  1 6 x  1 3x  1


1
6
5
4
 x x
5    x  1
3 7
x x
  4 .‫א‬
3 9
2
4
7
.‫ג‬
x x  x
3
5
15
2
3
 x  3   4  x   x  2 . ‫ה‬
5
15
.‫ב‬
.‫ד‬
.‫ו‬
1
x

 0 .‫ב‬
2 x 1
5
4

.‫ד‬
2 x  1 3x  2
1 2
  0 .‫א‬
4 x
3
1

.‫ג‬
x x2
x5 1 1


.‫ה‬
3x 2 6 x x
22
x2  2
3x  1
.‫א‬

2
3x  5 x 9 x  15
3
5

 0 .‫ג‬
2
 2  x  12  3x 2
7
2
3


 0 .‫ב‬
2
x 1 x  1 2  2x
4 x 2  24 x  36
 12 .‫ד‬
x 3
:‫מערכת שתי משוואות בשני נעלמים ממעלה ראשונה‬
5 x  2 y  14
.‫ב‬

5 x  3 y  23
x  3y  5
.‫א‬

x  3y  3
5 x  2 y  2
.‫ג‬

x  4 y  4
3x  2 y  16
.‫ב‬

 x  5 y  14
y  x 3
.‫ה‬

 y  2x  4
3x  y  11
.‫א‬

y  5
2 x  3 y  5
.‫ד‬

5 x  7 y  11
 x  3 x  y y 1



16
4
.‫ב‬
 8
3  2 x  y   4 x  11  0

3 y  x  2  4 x  2  3 y
.‫א‬

2 x  3  y  5 y  4 x  3
3
 3x  1 2
 4  5  x  y   10  x  3

 x 1  y  1
 4
2
.‫ג‬
7

4 x  y  3

.‫ג‬

2
5 x   7

y
3 3
x  y  2

.‫ב‬

9
4
   7
 x y
23
3 1
x  y  4

.‫א‬

5
1
  4
 x y
24
‫‪ )11‬פתור את המשוואות הבאות‪:‬‬
‫‪‬‬
‫‪ x  y  2   y  xy  5‬‬
‫א‪.‬‬
‫‪‬‬
‫‪‬‬
‫‪x  y  2‬‬
‫‪ xy  20‬‬
‫ב‪.‬‬
‫‪‬‬
‫‪ y  3x  4   20‬‬
‫‪5 x  4 xy  22‬‬
‫ג‪.‬‬
‫‪‬‬
‫‪6 x  xy  20‬‬
‫משוואות עם אינסוף פתרונות וללא פתרון‪:‬‬
‫א‪6  x  2   2 x  5  4 x .‬‬
‫ב‪5 x  3  x  4 x  2 x  3 .‬‬
‫‪‬‬
‫‪2  x  y   4 y  1  x‬‬
‫ד‪.‬‬
‫‪‬‬
‫‪2‬‬
‫‪‬‬
‫‪7‬‬
‫‪y‬‬
‫‪‬‬
‫‪x‬‬
‫‪‬‬
‫‪3‬‬
‫‪x‬‬
‫‪‬‬
‫‪y‬‬
‫‪‬‬
‫‪‬‬
‫‪‬‬
‫‪‬‬
‫‪x  2 y  1‬‬
‫ג‪.‬‬
‫‪‬‬
‫‪4 x  8 y  5‬‬
‫משוואה ממעלה שנייה‪:‬‬
‫א‪x2  3x  10  0 .‬‬
‫ב‪ x2  10 x  16  0 .‬‬
‫ד‪2 x 2  6 x  5  0 .‬‬
‫ג‪25x2  20 x  4  0 .‬‬
‫א‪4 x2  5x  7  4  x2  3 .‬‬
‫ב‪ x  x  5  1  3x 1  x   4 .‬‬
‫ג‪2  x  5   2 x  3  10 x  21 .‬‬
‫‪2‬‬
‫‪2‬‬
‫‪ )14‬פתור את המשוואות הבאות (משוואה חסרת ‪:) b‬‬
‫ב‪32 x2  18  0 .‬‬
‫א‪x2  36  0 .‬‬
‫‪ )15‬פתור את המשוואות הבאות (משוואה חסרת ‪:) c‬‬
‫ב‪5 x 2  x  0 .‬‬
‫א‪7 x2  14 x  0 .‬‬
‫‪25‬‬
4x 1 x  2 2
.‫א‬


3
2
x
3
2x  5
4


 0 .‫ג‬
2
2 x  2 2  x  1 1  x 2
x 9
 x  x 2  18 .‫ב‬
x3
2
:‫ריבועיות‬-‫משוואות ממעלה שלישית ומשוואות דו‬
x 4  3x 2  2  0 . ‫ב‬
5x4  3x2  8  0 .‫א‬
2 x3  5 x 2  2 x  5  0 . ‫ד‬
2 x3  7 x 2  7 x  2  0 . ‫ג‬
:‫משוואות עם פרמטרים‬
mx  3m  5x  1 .‫א‬
1
1
 a  3x    ax  3 .‫ב‬
3
a
 x  2a  x  2b   x2  2  a2  b2  .‫ג‬
m  1 m 1
.‫ד‬

x 1 x  1
x
1
ax  x
2

 3
 3
.‫ה‬
2
a  a 2a 2a  4a  2a a  2a 2  a
2
:‫) פתור את מערכות המשוואות הבאות‬19
ax  y  2
.‫ב‬

 x  ay  4
 x  my  1
.‫א‬

x  y  m

 m  1 x   2m  3 y  5
.‫ד‬


 m  2  x   2m  1 y  10m
x
 ym
.‫ג‬
m
 x  m2 y  1


 2a  b  x   2a  b  y  8ab
.‫ה‬

2
2

 2a  b  x   2a  b  y  8a  2b
26
:‫) פתור את המשוואות הריבועיות הבאות‬21
x2  2 x  4a  a 2  3 .‫ב‬
x2  2mx  m2  1  0 .‫א‬
1
1
1
 
 0 .‫ד‬
ax a ax
x2  m  x  10   2m2  5x .‫ג‬
a 1 x
  b
x b a
m
.‫ו‬
2
 1 x 2  m2 x  1  0 .‫ה‬
x
1 a b a b


x a b a b
.‫ז‬
:‫משוואות עם שורשים‬
x2  x
.‫ב‬
4x  3  5
.‫א‬
2 x  16  3 x  1
.‫ד‬
3x  1  x  13
.‫ג‬
x2  5x  12  2 6  x
.‫ו‬
3x  5  x  17
.‫ה‬
2x 1  3  7 x  1
.‫ח‬
x  1  2 x  5  11  x 2
.‫ז‬
2x  3  3  x  2
.‫י‬
9 x  8  3 x  4  2
.‫ט‬
2 x  2  5 x  4  3x  2
.‫יב‬
x  3  x  2  4 x  1 .‫יא‬
3 x 1  2 x  3  2 x  2
.‫יג‬
:‫משוואות עם ערך מוחלט‬
3x  24  x
.‫ב‬
2 x  11  7 .‫א‬
2 x  8  x  10
.‫ד‬
12  x  3x
.‫ג‬
14  3x  2 x  5
.‫ו‬
4 x  5  2 x  13
.‫ה‬
x  2  6  2x  4
.‫ח‬
x  7  2x
.‫ז‬
27
10  3x  x  4  2 x  6
x  2  2x  6  4x  8
.‫י‬
28
.‫ט‬
:‫מערכת משוואות ממעלה שנייה‬
:‫) פתור את מערכות המשוואות הבאות‬23
2 x 2  y 2  36
 2
 x  3 y  10
.‫ב‬
 x 2  y 2  20

x  y  6
.‫א‬
 x 2  2 y 2  17

 xy  10
.‫ד‬
3x 2  4 y 2  16
 2
2
5 x  3 y  17
.‫ג‬
2
2

 x  2 xy  8 y  8

2

3xy  2 y  4
.‫ו‬
 x 2  xy  20 y 2  0

x  6 y  1
.‫ה‬
16 x 2  y 2  391

4 x  y  23
.‫ח‬
 x 2  y 2  33

 x  y  11
.‫ז‬
3
3
 x  y  91
 2
2
 x y  xy  30
.‫י‬
 x3  y 3  243

x  y  9
.‫ט‬

 xy  24

2

 y  x   7  y  x   10  0
 x
y 10



x 3
 y
 2
2
 x  y  9 xy  25
3 5
 x  y  21

.‫יא‬

 8  1  13
 x y
.‫יב‬
2
2

 x y  xy  84
 2
2

 x  2 xy  y  5 x  5 y  24
.‫יד‬
.‫יג‬
1
.‫ ז‬x  3 .‫ ו‬x  2 .‫ ה‬x  2 .‫ ד‬x  8 .‫ ג‬x  0 .‫ ב‬x  1
2
1
1
. x  1 .‫ ו‬x  4 .‫ ה‬x  1 .‫ ד‬x  2 .‫ ג‬x  .‫ ב‬x  3
4
2
. x  21 .‫ ו‬x  10 .‫ ה‬x  1 .‫ ד‬x  1 .‫ ג‬x  30 .‫ ב‬x  18
. x  2 .‫ ה‬x  2 .‫ ד‬x  3 .‫ ג‬x  1 .‫ ב‬x  8
4
1
.   ,9  .‫ ב‬ 4,  .‫) א‬6 . x  6 , x  3 .‫ ד‬x  7 .‫ ג‬x  7 .‫ ב‬x  6
 5 
 3
.x
29
.‫) א‬1
.‫) א‬2
.‫) א‬3
.‫) א‬4
.‫) א‬5
.x
1
.‫ ז‬x  3 .‫ו‬
2
 7, 10 .‫ ה‬ 2,3 .‫ ד‬ 0,1 .‫ ג‬ 4, 2  .‫ ב‬ 2,5 .‫) א‬7
. 1,1 .‫ ג‬ 3,1 .‫ ב‬1,1 .‫) א‬9
 7, 2  .‫ ג‬ 7,1 .‫ ב‬ 6,5 .‫) א‬8
 2, 4  .‫ ג‬ 2,10  .‫ ב‬ 1, 3 .‫) א‬11
‫ אין פתרון למערכת המשוואות‬.‫ג‬
‫ אינסוף פתרונות‬.‫ אין פתרון ב‬.‫) א‬11
.‫ אינסוף פתרונות‬.‫ד‬
2
.‫ ג‬x1  2 , x2  8 .‫ ב‬x1  2 , x2  5 .‫) א‬12
5
1
. x1  1 , x2  10 .‫ ג‬x1  1 , x2  1 .‫ ב‬x1  0 , x2  1 .‫) א‬13
4
1
3
x1  0 , x2  .‫ ב‬x1  0 , x2  2 .‫) א‬15 x   .‫ ב‬x  6 .‫) א‬14
5
4
. x1  0 , x2  5 .‫ ג‬x  5 , x  3 .‫ ב‬x1  2 , x2  1.2 .‫) א‬16
.‫ אין פתרון למשוואה‬.‫ ד‬x 
. x1  1 , x2  1 , x3  2
1
1
.‫ ד‬x1  1 , x2  2 , x3  .‫ ג‬x  1 .‫ ב‬x  1 .‫) א‬17
2
2
a2  9
3m  1
.‫ ב‬x 
.‫) א‬18
6a
m5
m 1 
 2a  4 4a  2 
, 2
 2m  1, m  2 .‫ ד‬ m2  m  1,
 .‫ ב‬ m  1, 1 .‫) א‬19
 .‫ ג‬ 2
m 
 a 1 a 1 

. x  a  1 .‫ ה‬x  m .‫ ד‬x  a  b .‫ ג‬x 
x  m  5, 2m .‫ג‬
x  a  1,3  a .‫ב‬
x  m  1, m 1 .‫) א‬21
 2a  b, 2a  b  .‫ה‬
a b a b
a
1
.‫ ז‬x  , ab .‫ ו‬x  1,  2
.‫ ה‬x  a 3 .‫ד‬
,
a b a b
b
m 1
x  5 .‫ ח‬x  3 .‫ ז‬x  4, 3 .‫ ו‬x  6 .‫ ה‬x  5 .‫ ד‬x  8 .‫ ג‬x  2 .‫ ב‬x  7 .‫) א‬21
.x
8
9
. x  2 .‫ יג‬x  1 .‫ יב‬x  6 .‫ יא‬x  2, 2 .‫ י‬x  12 .‫ט‬
x  7 .‫ ז‬x  24,
4
1
.‫ ו‬x  9, 1 .‫ ה‬x  6 .‫ ד‬x  3 .‫ ג‬x  6,12 .‫ ב‬x  2,9 .‫) א‬22
5
3
1
. x  0 .‫ י‬x  0, 12 .‫ ט‬x  12, 1 .‫ח‬
3
.  5, 2 ,  5, 2  .‫ ד‬ 2, 1 .‫ ג‬ 4, 2  .‫ ב‬ 2, 4  ,  4, 2  .‫) א‬23
.  5, 3 .‫ ח‬ 7, 4  .‫ז‬
1
1  5 1 
 1 

 3,  ,  3,   ,  2,1 ,  2, 1 .‫ ו‬ 2,  ,  ,  .‫ה‬
2
2   11 11 
 2 

1 1
.  ,  .‫ יא‬ 6,5 ,  5, 6  .‫ י‬ 3,6  ,  6,3 .‫ט‬
 2 3
.  4,6 ,  6, 4 ,  3,8 ,  8, 3 .‫יב‬
.  1.65,6.35 ,  6.35,1.65  7, 4  ,  4, 7  .‫יג‬
30
.  5, 45 ,  5, 45 ,  45,5 ,  45, 5 .‫יד‬
31
‫אי שוויוניים‪:‬‬
‫מה מותר?‬
‫‪ .1‬לחבר או לחסר כל מספר או ביטוי‪.‬‬
‫‪ .2‬לכפול או לחלק בכל מספר או ביטוי חיובי‪.‬‬
‫מה אסור?‬
‫‪ .1‬לכפול או לחלק בביטוי שלא יודעים‬
‫את סימנו‪.‬‬
‫‪ .2‬להעלות בחזקה זוגית כשיש אגף‬
‫שלילי‪.‬‬
‫‪ .3‬לכפול או לחלק בכל מספר או ביטוי שלילי‬
‫תוך הפיכת סימן אי‪-‬השוויון‪.‬‬
‫‪ .4‬להעלות בחזקה אי זוגית‪.‬‬
‫‪ .5‬להעלות בחזקה זוגית אם שני אגפי‬
‫אי‪-‬השוויון אינם שליליים‪.‬‬
‫אי‪-‬שוויונים ממעלה ראשונה‪:‬‬
‫פתור את אי‪-‬השוויונים הבאים‪:‬‬
‫‪45x  26  109 )1‬‬
‫‪)3‬‬
‫‪)5‬‬
‫‪)7‬‬
‫‪1‬‬
‫‪ 4x  6‬‬
‫‪2‬‬
‫‪8 x  4 9  x  1‬‬
‫‪‬‬
‫‪2‬‬
‫‪3‬‬
‫‪x6 x4‬‬
‫‪‬‬
‫‪ 12  x‬‬
‫‪3‬‬
‫‪4‬‬
‫‪2  x  5 ‬‬
‫‪)2‬‬
‫‪6 x  2  3x  1‬‬
‫‪)4‬‬
‫‪ 4   x  2   20‬‬
‫‪)6‬‬
‫‪4  6 x  8   8  3x  4 ‬‬
‫‪)8‬‬
‫‪7  x 3x  1 x  4‬‬
‫‪‬‬
‫‪‬‬
‫‪7‬‬
‫‪10‬‬
‫‪5‬‬
‫‪3‬‬
‫‪2‬‬
‫‪2‬‬
‫‪ x  2‬‬
‫אי‪-‬שוויונים ממעלה שנייה‪:‬‬
‫פתור את אי‪-‬השוויונים הבאים‪:‬‬
‫‪)9‬‬
‫‪x 2  144‬‬
‫‪)11‬‬
‫‪x  12 x  32‬‬
‫‪2‬‬
‫‪ x  2 x  5  0 )11‬‬
‫‪ x  2 x  4  35 )12‬‬
‫‪ x2  13x  30  0 )13‬‬
‫‪ x  3 x  7   8x  56 )14‬‬
‫‪)15‬‬
‫‪ x  x  2   89‬‬
‫‪)17‬‬
‫‪3x2  12 x  0‬‬
‫‪)19‬‬
‫‪  x  1 x  6   x 2  3x‬‬
‫‪2‬‬
‫‪ x  5‬‬
‫‪2‬‬
‫‪ x  3‬‬
‫‪32‬‬
‫‪ 4  x  3‬‬
‫‪2‬‬
‫‪ 5x  6‬‬
‫‪)16‬‬
‫‪2‬‬
‫‪)18‬‬
‫‪x2  10 x  25  0‬‬
‫‪)21‬‬
‫‪2 x2  2 x  24  0‬‬
33
:‫שוויונים ממעלה שלישית‬-‫אי‬
:‫השוויונים הבאים‬-‫פתור את אי‬
 x 1 x  2 x  3  0 )21
x  x 2  x  1  0 )22
x
2
x3  25x  0 )24
 2x
 8x  20   3x  5  0 )26
x
x3  6 x 2  9 x  0
2
 3x  2   x  1  0
)23
2
 3x  5   x  2   0
)25
x
)28
2
 x  6   x  1  0 )27
x
 x  2 x  4 x 1  0 )31
2
 6   x  3  0 )29
:‫שוויונים עם מנה‬-‫אי‬
x 1
 0 )31
x2  9
x 1
 3 )32
3x  2
x 3
 0 )34
2 x  10 x  12
1
0
x  16
)33
1
0
3  x  1
2x 1
0
x 5
)35
2
2
)36
1
 0 )38
x  5x  6
x 1
 1 )37
x2
1
 0 )41
2
x  8 x  12
x2  7 x  6
 0 )39
 x 2  3x  7
2
:‫ מערכת וגם‬- ‫שוויונים כפולים‬-‫אי‬
0
0
6
1
 2 )42
x4
3  x  1  5 )41
8  3x
 4 )44
5  2x
2 x  10 7 x  20

)46
3
5
4 x  5 3x  8 9  x


 11 )48
15
5
3
34
1 
x 1
 1 )43
x 1
6x  38  x  3  5x  7 )45
1 
2x  6 x  2

4
3
)47
35
:‫שוויונים‬-‫שאלות מסכמות – אי‬
x  x  5  3x  15  2 x  1  x(4  x) )51
x
 x  5 3x  1  0 )52
 2  x  x  7 
 x  4  x  2   0 )51
x 1
 2 x  3 x  12   0 )53
 x  1 4  x 
x  x  3 2 x  5  0 )54
5  2x
 x  8
2
3
 2  x  5  0  x  8 )49
4
 x  6   x  1  0 )55
2
 0 )56
x2
x 3
 0 )57
x2  2
x  4x
 0 )58
x  2x  3
x7
 0 )61
2
x  x3
2
2
x2  6x  9
 0 )59
x3  x
x
1
1
)61


2
x 4 x2 x2
2 x2
x
x
)62


2
x  6x  8 x  4 x  2
3
2
1
1
 0 

)64
x 1 x
x  3 1 x
x2  3x  10  6  5x  x 2 )63
1
? g  x 
x 1
 2 )65
x4
x 1
x
‫ מעל הפונקציה‬f  x  
‫ נמצאת הפונקציה‬x ‫) לאלו ערכי‬66
x3
x 3
. x  13 )8 x  12 )7 x ‫) אף‬6 x  5 )5 x  2 )4 x ‫) אף‬3 x ‫) כל‬2 x  3 )1
. 9  x  3 )12 5  x  2 )11 x  4 , x  8 )11 12  x  12 )9
. 4  x  0 )16 4  x  8 )15 x  7 , x  11 )14 x  2 , x  15 )13
. x ‫) כל‬21 x  3 , x  5 )19 x  5 , x  5 )18 0  x  4 )17
1
)23 x  0 )22 1  x  2 ‫ או‬x  3 )21
2
2
. x  3 )29 x  0 , x  3 )28 x  2 , 1  x  3 )27 x  1 )26 x  2 )25
3
2
1
. x   , x  )32 3  x  1 , x  3 )31 x  1 , 2  x  4 )31
3
2
5  x  0 , x  5 )24 2  x  1 , x 
36
. x  2 )37 x  1 )36
1
 x  5 )35 2  x  3 , x  3 )34 x  4 , x  4 )33
2
1
2
. x  0 )43 x  3 )42 2  x  4 )41 x  2 , x  6 )41 1  x  6 )39 2  x  3 )38
3
5
2
2
)49 .  )48 1  x  13 )47 x  10 )46   x  7 )45 x  2 , x  2 )44
3
5
3
4
1
x  7 ,   x  2 , 5  x )52 x  2 , 1  x  4 )51 x  4 )51
3
.8 x  1 , 2  x  6 , 6  x )55 x  3 , 0  x  2.5 )54 . 1  x  1.5 , 4  x  12 )53
. x  3 , 0  x  1 , x  4 )58 3  x )57 2.5  x  8 , 8  x )56
. x  2 , 2  x  4 )61 7  x )61 1  x  0 , 1  x  3 , 3  x )59
. x  7 )65 x  1 )64 x ‫) אף‬63 x  0 , 1  x  2 , 4  x )62
3
. 3  x   , 3  x )66
5
2  x  
:‫תחום הגדרה‬
:‫) מצא את תחום ההגדרה של הפונקציות הבאות‬1
f  x  2 x  3
.‫ב‬
f  x  x
.‫א‬
5x
x4
x2
.‫ד‬
f  x   3x 1  2 x
.‫ג‬
.‫ו‬
f  x   x 2  3x  10
.‫ה‬
x 1
x 2 x
.‫ז‬
f  x 
f  x 
x3  9 x
f  x 
:‫) מצא את תחום ההגדרה של הפונקציות הבאות‬2
f  x 
1
x x6
x2  5x  6
f  x 
x 1
f  x 
.‫ב‬
f  x 
.‫ד‬
x  2 3
.‫א‬
2x2  x  3
x2  5x  9
.‫ג‬
x  5 , x  2 .‫ ה‬x  4 .‫ ד‬x 
1
.‫ ג‬x  3 .‫ ב‬x  0 .‫) א‬1
2
. x  2 , 2  x  1 , 1  x  2 .‫ ז‬3  x  0 , x  3 .‫ו‬
37
1
2
. x  3 , 2  x  1 .‫ ד‬x  1 , x  1 .‫ ג‬6  x  2 .‫ ב‬x  7 .‫) א‬2
38
:‫ – חוקי חזקות ומשוואות מעריכיות ולוגריתמיות‬3 ‫פרק‬
:‫חוקי חזקות‬
:‫סיכום חוקי החזקות‬
a n  a m  a nm
a  b  a  b
m
m
a
 
b
m
b
 
a
a1  a
.3
m
a 
n m
.6
m
a
am 
.9
n m
1
am
a 0  1 .1
.2
.5
an
 a nm
m
a
.8
am  a 
 
bm  b 
.4
m
.7
:‫סיכום חוקי השורשים‬
n
m
1
an  a m
n m
.3
a  m n a
1
a  am
.2
a ma

m
b
b
.5
m
a  a2
m
.6
a  m b  m a b
m
.1
.4
:‫שאלות יסודיות – חוקי חזקות ושורשים‬
:‫) חשב ללא מחשבון את ערכי הביטויים הבאים‬1
93  27 2
39  81
.‫ב‬
23  25
.‫ד‬
23  2 7
2 4  25
109  255  81
403 1255
.‫א‬
.‫ג‬
:‫) פשט את הביטויים הבאים‬2
k 
k 
 2a b    ab 
2 m 2
 k 13m
3
1
 7 m4
k
.‫ב‬
1 x n 3  x n 5

x2
x n2
.‫ד‬
2m
5
.
2
3
3 2
4
 a2 
4ab   
 b 
4b 3
4b 1  4b  2
.‫א‬
2
.‫ג‬
22  8
:‫) חשב ללא מחשבון את ערך הביטוי הבא‬3
5
128
39
:‫) הכנס לתוך שורש את המספרים החופשיים‬4
36
2
63
.‫ג‬
5 3
.‫ב‬
3 2
.‫א‬
x x
.‫ה‬
23 3
.‫ד‬
:‫) הוצא מהשורש את הכופל הגדול ביותר‬5
48 .‫ב‬
12 .‫א‬
.‫ג‬
3
.‫ה‬
x5
54
.‫ד‬
:‫משוואות מעריכיות‬
. x  y :‫ הוא‬a x  a y :‫ פתרון כללי של משוואת מעריכית מהצורה‬.1
. a x  1  a0 :‫ שכן‬x  0 :‫ הוא‬a x  1 :‫ פתרון של משוואה מהצורה‬.2
‫ ללא תלות‬a x  b x  1 :‫ שכן‬x  0 :‫ הוא‬a x  b x :‫ פתרון של משוואה מהצורה‬.3
.‫בבסיסים‬
:‫שאלות יסודיות – משוואות מעריכיות‬
:‫פתור את המשוואות הבאות‬
 25  0.2 
2x 2
1 x
 1 


 125 
1
2  32   
8
)8
2x
13 x
e  e
x
3 x 1
1
 x 
e 
)13
2  6 x  6 x  2  6 x 1  227 )17
5  3x  3x1  162 )16
22 x  6  2 x  8  0 )21
e2  e x  e x 1  e  1 )19
x
4 5 3
    
9 2 2
 x 1
35 x 3  33 x  7 )6
)7
1
27     9 3 )11
3
3x  5x )11
2 x  2 x  16 )14
x
2x
3
 
4
2 x
3x
4
9
    
3
 16 
 1 
53 x  

 8
7 x
)9
2 x /3 2
)12
e x  2e x  3e4 )15
1 x

2
5 x  25 2
 5 x 1  145 )18
2
)23
3
6 x  4  6 x  3  0 )22
5  25x  26  5x  5  0 )21
e1 x  e1 x  e2  1 )26
e2 x  e x  2  0 )25
20
8
)24
 3 x
9 1
9 1

40
x
‫תשובות סופיות‪:‬‬
‫‪2b3‬‬
‫‪1‬‬
‫‪5‬‬
‫‪1‬‬
‫‪ .‬ב‪ . k .‬ג‪.‬‬
‫‪ )1‬א‪ . 2 .‬ב‪ . .‬ג‪ . .‬ד‪ )2 . 40 .‬א‪.‬‬
‫‪a‬‬
‫‪5‬‬
‫‪8‬‬
‫‪3‬‬
‫‪1‬‬
‫‪x‬‬
‫‪ . 3‬ד‪. 2 )3 .  x .‬‬
‫‪ )4‬א‪ . 18 .‬ב‪ . 75 .‬ג‪ . 9 .‬ד‪ . 3 24 .‬ה‪. x3 .‬‬
‫‪ )5‬א‪ . 2 3 .‬ב‪ . 4 3 .‬ג‪ . 3 7 .‬ד‪ . 3 3 2 .‬ה‪. x  1 )7 . x  5 )6 . x 2 x .‬‬
‫‪1‬‬
‫‪1‬‬
‫‪)13 . x  3 )12 . x  0 )11 . x   )11 . x  2 )9 . x  1 )8‬‬
‫‪6‬‬
‫‪2‬‬
‫‪. x  1, 2 )21 . x  1 )19 . x  2 )18 . x  1 )17 . x  4 )16 . x  4 )15 . x  3‬‬
‫‪)14 . x  1,‬‬
‫‪. x  1 )21‬‬
‫‪1‬‬
‫‪)24 . x  0,1 )23 . x  0 )22‬‬
‫‪2‬‬
‫‪. x  1 )26 . x  0 )25 . x  1, ‬‬
‫משוואות לוגריתמיות‪:‬‬
‫‪ .1‬הגדרת הלוגריתם‪ a x  b  loga b  x :‬כאשר‪. a , b  0 , a  1 :‬‬
‫לוגריתם על בסיס ‪ a‬של ‪ b‬מוגדר כחזקה שיש להעלות את ‪ a‬על מנת שיהיה‬
‫שווה ל‪ . b -‬ערך חזקה זו הוא ‪ . x‬ערך לוגריתם יכול להיות חיובי‪ ,‬שלילי או‬
‫אפס‪ .‬נפתור משוואות לוגריתמיות ע"י מעבר לפי ההג דרה למשוואה מעריכית‬
‫מתאימה‪.‬‬
‫‪ .2‬דוגמאות כלליות‪:‬‬
‫‪. 23  8  log 2 8  3 ‬‬
‫‪. 34  81  log3 81  4 ‬‬
‫‪. 102  100  log10 100  2 ‬‬
‫‪. 16  4  log16 4  0.5 ‬‬
‫‪‬‬
‫‪1‬‬
‫‪1‬‬
‫‪ log5‬‬
‫‪ 2‬‬
‫‪25‬‬
‫‪25‬‬
‫‪. 52 ‬‬
‫‪. 60  1  log6 1  0 ‬‬
‫‪ .3‬חוקי יסוד בלוגריתמים‪:‬‬
‫א‪log a a  1 .‬‬
‫ב‪. log a 1  0 .‬‬
‫‪ .4‬חוקי הלוגריתמים‪:‬‬
‫א‪ .‬מכפלה לסכום‪. log a  x  y   log a x  log a y :‬‬
‫‪x‬‬
‫ב‪ .‬מנה להפרש‪. log a    log a x  log a y :‬‬
‫‪y‬‬
‫‪ ‬‬
‫ג‪ .‬מקדם למעריך‪. loga bn  n loga b :‬‬
‫‪41‬‬
‫‪ .5‬חזקה לוגריתמית‪. alog x  x :‬‬
‫‪a‬‬
‫‪log m b‬‬
‫‪ .6‬מעבר מבסיס לבסיס‪:‬‬
‫‪log m a‬‬
‫‪ , log a b ‬כאשר‪. a , m  0 ; a , m  1 ; b  0 :‬‬
‫‪ .7‬לוגריתם על בסיס ‪ e‬נקרא הלוגריתם הטבעי ומסומן‪. loge x  ln x :‬‬
‫שאלות יסודיות – חוקי הלוגריתמים ומשוואות לוגריתמיות‪:‬‬
‫‪ )1‬חשב ללא מחשבון את ערכי הביטויים הלוגריתמים הבאים‪:‬‬
‫ג‪log 25 5 .‬‬
‫א‪log 2 32 .‬‬
‫ב‪log1000 .‬‬
‫ד‪.‬‬
‫‪log8 4‬‬
‫ז‪.‬‬
‫‪1‬‬
‫‪a a‬‬
‫ה‪.‬‬
‫‪1‬‬
‫‪16‬‬
‫ו‪.‬‬
‫‪log 4‬‬
‫‪log a a 4‬‬
‫‪log a‬‬
‫‪ )2‬חשב ללא מחשבון את ערכי הביטויים הלוגריתמיים הטבעיים הבאים‪:‬‬
‫א‪.‬‬
‫ב‪.‬‬
‫‪ln e 2‬‬
‫‪1‬‬
‫‪e4‬‬
‫ג‪.‬‬
‫‪ln‬‬
‫‪1‬‬
‫‪e e‬‬
‫‪ln‬‬
‫‪ )3‬פתור את המשוואות הלוגריתמיות הבאות (שימוש בהגדרת הלוג)‪:‬‬
‫ב‪log 2 x  16 .‬‬
‫א‪log36 6  x .‬‬
‫ג‪.‬‬
‫‪log 1 x  1.5‬‬
‫ד‪.‬‬
‫‪9‬‬
‫‪log x 64  3‬‬
‫ה‪.‬‬
‫‪log x 25  2‬‬
‫ו‪.‬‬
‫‪log x  3x  4   2‬‬
‫ז‪.‬‬
‫‪ln x  2‬‬
‫ח‪.‬‬
‫‪1‬‬
‫‪2‬‬
‫‪ln x  ‬‬
‫‪ )4‬חשב ללא מחשבון את ערכי הביטויים הבאים (שימוש בחוקי הלוגים)‪:‬‬
‫ב‪2log 2  log 25 .‬‬
‫א‪log6 8  log6 9  log6 2 .‬‬
‫ג‪.‬‬
‫‪log3 2  log3 4‬‬
‫‪3log3 6   2  log 3 12 ‬‬
‫‪42‬‬
‫‪ )5‬נתון‪ . log3 2  a :‬הבע באמצעות ‪ a‬את ערכי הביטויים הבאים‪:‬‬
‫א‪.‬‬
‫‪log3 16‬‬
‫ב‪log3 6 .‬‬
‫ד‪. log3 1.5 .‬‬
‫ג‪log3 24 .‬‬
‫‪ )6‬נתון‪ . log2 3  a , log 2 5  b :‬הבע באמצעות ‪ a‬ו‪ b -‬את ערכי הביטויים הבאים‪:‬‬
‫א‪log 2 45 .‬‬
‫ב‪log 2 60 .‬‬
‫ג‪. log 2 7.5 .‬‬
‫‪ )7‬חשב ללא מחשבון את ערכי הביטויים הבאים (חזקה לוגריתמית)‪:‬‬
‫ב‪4log 5 .‬‬
‫ד‪. e2 ln 3 .‬‬
‫ג‪eln 3 .‬‬
‫א‪6log 8 .‬‬
‫‪6‬‬
‫‪2‬‬
‫‪ )8‬נתון‪ . log2 3  a , log3 5  b :‬הבע באמצעות ‪ a‬ו‪ b -‬את ערכי הביטויים הבאים‪:‬‬
‫א‪log3 50 .‬‬
‫ב‪log 2 30 .‬‬
‫ג‪log5 22.5 .‬‬
‫‪ )9‬פתור את המשוואות הלוגריתמיות הבאות (שימוש בהגדרת הלוג מספר‬
‫פעמים)‪:‬‬
‫‪‬‬
‫‪‬‬
‫א‪.‬‬
‫‪log x  x 2  6 x   3‬‬
‫ב‪.‬‬
‫‪log3 log x  x 2  6 x   1‬‬
‫ג‪.‬‬
‫‪log5 log 2  x 2  7   0‬‬
‫‪‬‬
‫ד‪.‬‬
‫‪log5  25x  20   x‬‬
‫‪‬‬
‫‪ )11‬פתור את המשוואות הלוגריתמיות הבאות (שימוש בחוקי הלוגריתמים)‪:‬‬
‫א‪.‬‬
‫‪1‬‬
‫‪‬‬
‫‪ln  e2 x    ln 2  x‬‬
‫‪2‬‬
‫‪‬‬
‫ג‪.‬‬
‫‪2log 2  2 x  2   log 2 16  x   log 2  x  1  1‬‬
‫ב‪.‬‬
‫‪log5  4 x  3  log5 7‬‬
‫‪ )11‬פתור את המשוואות הלוגריתמיות הבאות (הצבת ‪ t‬וקבלת משוואה ריבועית)‪:‬‬
‫ב‪3ln 2 x  ln x  2 .‬‬
‫א‪log 22 x  log 2 x  2  0 .‬‬
‫ג‪.‬‬
‫ה‪.‬‬
‫‪log 4 x  log x 4  2.5‬‬
‫‪1‬‬
‫‪ ln  ex 2 ‬‬
‫‪x‬‬
‫ד‪.‬‬
‫‪ln  e2 x3   ln‬‬
‫‪43‬‬
‫‪log x  log x 10 x   2‬‬
:)‫) פתור את המשוואות הלוגריתמיות הבאות (הוצאת לוג משני אגפי המשוואה‬12
25
x
.‫ב‬
x log3 x  81
.‫א‬
4
x
.‫ד‬
x ln x  e6 x
.‫ג‬
1
  x1ln x
e
.‫ו‬
log5 x  x  1
1
1 
log5 x  x  1
log 5 x  x  1
.‫ה‬
x log5 x 
x
1
 
 x
2 3ln x
log 2 x 6
4

:)‫) פתור את המשוואות הלוגריתמיות הבאות (בסיסים שונים‬13
e  2 .‫ג‬
5 x  8 .‫ב‬
2 x  5 .‫א‬
x
e x  1
.‫ה‬
ex 
1
2
.‫ד‬
2
1
.‫ ד‬. .‫ ג‬.3 .‫ ב‬.5 .‫) א‬1
3
2
1
. x  e2 .‫ ז‬. x  4 .‫ ו‬. x  5 .‫ ה‬. x  4 .‫ ד‬. x  27 .‫ ג‬. x  65,536 .‫ ב‬. x  .‫) א‬3
2
1
.1  a .‫ ד‬.3a  1 .‫ ג‬. a  1 .‫ ב‬. 4a .‫) א‬5 .3 .‫ ג‬. 2 .‫ ב‬. 2 .‫) א‬4 . x 
.‫ח‬
e
1
1
1
.9 .‫ ד‬.3 .‫ ג‬. 25 .‫ ב‬.8 .‫) א‬7 . a  b  .‫ ג‬. 2  a  b .‫ ב‬. 2a  b .‫) א‬6
2
2
2
2
1
1 a ab
1
. 1
.‫ ג‬.  
.‫ ב‬. 2b  .‫) א‬8
b
ab
2 2 2
a
. x  1 .‫ ד‬. x  3 .‫ ג‬. x  3 .‫ ב‬. x  3 .‫) א‬9
. x  6 .‫ ג‬. x  2.5 .‫ ב‬. x  0 .‫) א‬11
1
1
1
1 1
,10 .‫ ד‬. x  16, 2 .‫ ג‬. x  3 e2 , .‫ ב‬. x  4, .‫) א‬11
. x  3 , .‫ ה‬. x 
100
e
2
e e
. 1.5 .‫ ג‬. 4 .‫ ב‬. 2 .‫) א‬2 . 1.5 .‫ ז‬.4 .‫ ו‬. 2 .‫ ה‬.
1
4
1
1
1
x
,5 .‫ ב‬. x  9, .‫) א‬12
2 .‫ ג‬.
e
25
9
.  .‫ ה‬. x  0.693 .‫ ד‬. x  0.693 .‫ ג‬. x  1.292 .‫ ב‬. x  2.322 .‫) א‬13
. x  e , e .‫ ו‬. x  3 .‫ ה‬. x  16, .‫ ד‬. x  e3 ,
44
:‫אי שוויונים מעריכיים‬
. 0  a  1 :‫ עבור‬x  y - ‫ ו‬a  1 :‫ עבור‬x  y :‫ הוא‬a x  a y :‫השוויון‬- ‫פתרון אי‬
:‫פתור את אי השיוויונים הבאים‬
2 4
x
x 2 1
1
4
1
1 x
3
32 x 1  27
)2
e  3 )4
x
e
5x
25  5  6  5
x
x
x 1
 e 2 x )3
13 x
1
1
   
7
7
)6
e2 x  2e x  1  0 )8
)1
)5
e2 x  5e x  4  0 )7
x
1
)5
8
x  ln 3 )4
0  x  1 )3
. x  0 )8
1
2
x  1  1  x )2 x  )1
4
3
x  0  ln 4  x )7 0  x  1 )6
:‫שוויונים לוגריתמיים‬-‫אי‬
. 0  a  1 :‫ עבור‬x  y - ‫ ו‬a  1 :‫ עבור‬x  y :‫ הוא‬loga x  log a y :‫השוויון‬- ‫פתרון אי‬
log6  x 2  5 x   1 )2
log 2 x  log 2  5x  20  )1
log 1 1  3x   log 1  7  x  )4
log3 x  log9 15  2 x  )3
2
2
ln x  3 )6
ln x  ln  x 2  12  )5
6
1
 2
)8
2
ln x
ln x
ln 2 x  6ln x  7 )7
2 3  x  4 )5 3  x 
1
1
)4 3  x  7 )3 1  x  0 , 5  x  6 )2 x  5 )1
3
2
. x  1 ‫וגם‬
1
e3
45
 x  e 2 )8
1
 x  e7 )7 0  x  e3 )6
e
:‫תירגול נוסף‬
:‫חזרה על חוקי חזקות ושורשים‬
: a n a m  a nm ,
an
 a n m :‫פשט את הביטויים הבאים לפי הכללים‬
am
a12 a 2 a 4 a3 )3
a 4 a 5 a 9 )2
a 2 a 6 )1
a 3a8
)6
a4
a16
a7
)5
a8
a3
a 2b3a8b12
)9
a 7 b9
323334 )12
b10b12
b 2b 6b 7
)8
b 2 b 7 b3
)7
b 5b 4
)4
26 22 )11
a16b 4 a10b8 a 6b12
)11
a3b5 a 2b 2 a 4
217 35
)14
21434
316
)13
314
31952456
)17
530318
46 7 4 7 3
)16
7 6 4 4 43
21251336
)15
2936512
:  a n   a nm :‫פשט את הביטויים הבאים לפי הכלל‬
m
a  a 
a  a 
a  a 
 a  b  a
2 4
3 3
7 2
2 8
4 6
6 2
2 3
6 5
12
a 23b 28
 2  3 
4 5
5 7
335 240
)23
220
)26
)29
a 
a 
6 4
)21
a2
a 
2 6
)19
5
8 2
a14
3  3
3  3
3  5 3
5  5 3
5 3
2
3 2
4
2 6
31 7
2 10
11 18
 a13 
 4  )21
a 
)22
2 
3 4
)25
2 2 29
a 20  a 3   b5 
4
)28
a 30b15  b3 
3 
2 7
)24
6
)27
5
510  53 
39516
46
)18
2
)31
n
 
:  ab   a nbn ,    n :‫פשט את הבאים לפי הכללים‬
b
b
a
n
a b 
4 8 4
an
a b 
6 3 2
)33
2
 a8 
 2  )35
b 
 a 2 a 7b9 
 3 6 4  )39
b a b 
30
 a 6b10 
 3 4 5  )38
a b b 
  54 2 36 

 )42
 35  57 


2 3 
 18 39  )41
3 2 
 a 3b7 
 4  )36
 b 
2
40 20
 a b
2
)32
3
)31
4
 a5 
 4  )34
b 
3
12
 a 4b10 
 3 8  )37
ab 
20
  a 2 3 b 20 

 )41
 a 5  b 2 7 


3
3
2
 35 26 22 
 6 5 2  )43
3 2 3 
:a
n
1
a
 n ,  
a
b
n
60  33 )46
6
 
5
b
 
a
n
:‫פשט את הבאים לפי הכללים‬
32 )44
23 )45
2
1
)49
1
  )48
3
 4
   )52
 5
 2
   )51
 3
 4
   )51
 7
)55
 ab  )54
 2433 
 2  )53
 32 


a 24b 25

 )58
  a 3 6  b 2 2 b 20 


  a 2 4 a 3b12b 4 

 )57


a11b15


2
 a4 
 3
b 
3

5
1024
4
3
4
1
 24 )47
2
3
2
5
3
 a 4 a 2b 6 

 )56
6
 ab 
8
:)‫) חשב ללא מחשבון את ערכי הביטויים הבאים (שורשים‬59
 25 .‫ב‬
49 .‫א‬
.‫ג‬

.‫ו‬
2
252
.‫ט‬
3
 2 
4
6
16
47
 7 128
.‫ה‬
.‫ח‬

5
243

3
.‫ד‬
.‫ז‬
‫י‪.‬‬
‫יג‪.‬‬
‫‪2‬‬
‫‪2‬‬
‫‪ 25‬‬
‫‪‬‬
‫טז‪.‬‬
‫‪2  32‬‬
‫יט‪.‬‬
‫‪16  7 8‬‬
‫יא‪.‬‬
‫‪4‬‬
‫‪1000‬‬
‫‪84‬‬
‫‪3‬‬
‫‪‬‬
‫‪ 1000 ‬‬
‫‪6‬‬
‫טו‪.‬‬
‫‪2  18‬‬
‫יז‪.‬‬
‫‪4  5  20‬‬
‫יח‪.‬‬
‫‪9  5 27‬‬
‫כ‪.‬‬
‫‪72‬‬
‫‪2‬‬
‫כא‪.‬‬
‫‪2‬‬
‫יד‪.‬‬
‫‪7‬‬
‫‪6‬‬
‫יב‪.‬‬
‫‪3‬‬
‫‪‬‬
‫‪32‬‬
‫‪5‬‬
‫‪81‬‬
‫‪3‬‬
‫‪‬‬
‫‪5‬‬
‫‪3‬‬
‫‪3‬‬
‫‪ )61‬הכנס לתוך השורש את המקדם שלפניו‪:‬‬
‫א‪.‬‬
‫‪5 2‬‬
‫ב‪.‬‬
‫‪3 6‬‬
‫ג‪.‬‬
‫‪24‬‬
‫‪2‬‬
‫ד‪.‬‬
‫‪75‬‬
‫‪5‬‬
‫ה‪.‬‬
‫‪4 300‬‬
‫‪10‬‬
‫ו‪.‬‬
‫‪34 7‬‬
‫ז‪.‬‬
‫‪45 3‬‬
‫ח‪.‬‬
‫‪2 3 20‬‬
‫‪5‬‬
‫‪ )61‬הוצא מתוך השורש את השלם הגדול ביותר‪:‬‬
‫ג‪.‬‬
‫ב‪50 .‬‬
‫א‪40 .‬‬
‫‪3‬‬
‫ז‪.‬‬
‫ו‪108 .‬‬
‫ה‪250 .‬‬
‫‪5‬‬
‫‪4‬‬
‫י‪162 .‬‬
‫ט‪972 .‬‬
‫ד‪.‬‬
‫ח‪.‬‬
‫‪320‬‬
‫‪56‬‬
‫‪3‬‬
‫‪90‬‬
‫‪160‬‬
‫‪5‬‬
‫‪ )62‬חשב ללא מחשבון את ערכי הביטויים הבאים‪:‬‬
‫‪2‬‬
‫א‪.‬‬
‫ה‪.‬‬
‫ב‪.‬‬
‫‪83‬‬
‫‪1‬‬
‫‪3‬‬
‫‪‬‬
‫‪3‬‬
‫‪4‬‬
‫‪81  64‬‬
‫ו‪.‬‬
‫‪3‬‬
‫‪5‬‬
‫‪‬‬
‫‪1‬‬
‫‪2‬‬
‫‪1.5‬‬
‫‪ 1 ‬‬
‫‪ ‬‬
‫‪ 25 ‬‬
‫‪‬‬
‫‪1‬‬
‫‪3‬‬
‫ג‪.‬‬
‫‪32‬‬
‫‪2‬‬
‫‪3‬‬
‫‪‬‬
‫‪343 100‬‬
‫ז‪.‬‬
‫‪1‬‬
‫‪2‬‬
‫‪‬‬
‫ד‪.‬‬
‫‪5‬‬
‫‪‬‬
‫‪2‬‬
‫‪ 1‬‬
‫‪2 ‬‬
‫‪ 4‬‬
‫‪1‬‬
‫‪4‬‬
‫‪16  8  4‬‬
‫‪256 )11 a 23b17 )11 a3b6 )9 b 7 )8 b3 )7 a 7 )6 a 9 )5 a 5 )4 a 21 )3 a18 )2 a 8 )1‬‬
‫‪a 4 )22 a 45 )21 a 23 )21 a 24 )19 a12 )18 3 )17 7/4 )16 40 )15 24 )14 9 )13 39 )12‬‬
‫‪b2‬‬
‫‪)26 37 )25 2 )24 a 22 )23‬‬
‫‪3‬‬
‫‪a‬‬
‫‪a 32‬‬
‫‪a15‬‬
‫)‬
‫‪35‬‬
‫‪)34‬‬
‫‪b8‬‬
‫‪b12‬‬
‫‪a16b32 )33 a12b6 )32 a 6b3 )31 35 )31 1 )29 3 )28 a 2 )27‬‬
‫‪225 )42 5832 )41 a3b18 )41 a90b60 )39 a36b12 )38 a 20b40 )37 a 6b6 )36‬‬
‫‪48‬‬
25
27
49
25
1
1
1
1
64
)52 
)51
)51
)49 3 )48  )47
)46
)45 )44
)43
8
16
27
8
9
729
16
36
16
1
1
1
1
1
b12
)
58
)
57
)
56
)55 2 2 )54 6 )53
6
5
15
16
ab
b
a
ab
6
a
-8 .‫ יב‬ .‫ יא‬5 .‫ י‬ .‫ ט‬ .‫ ח‬- 27 .‫ ז‬16 .‫ ו‬4 .‫ה‬
-2 .‫ ד‬2 .‫ ג‬- 5 .‫ ב‬7 .‫) א‬59
10 .‫ יד‬100 .‫יג‬
.3 .‫ כא‬6 .‫ כ‬2 .‫ יט‬3 .‫ יח‬20 .‫ יז‬8 .‫ טז‬6 .‫טו‬
32
.‫ח‬
25
.3
5
3072 .‫ז‬
4
567 .‫ו‬
48 .‫ה‬
3 .‫ד‬
6 .‫ג‬
54 .‫ב‬
50 .‫) א‬61
. 3 4 2 .‫ י‬3 5 4 .‫ ט‬2 5 5 .‫ ח‬2 3 7 .‫ ז‬3 3 4 .‫ ו‬5 10 .‫ ה‬3 10 .‫ ד‬8 5 .‫ ג‬5 2 .‫ ב‬2 10 .‫) א‬61
.
1
10
27
32
1
.‫ז‬
.‫ו‬
.‫ה‬
.‫ ד‬125 .‫ג‬
.‫ב‬
2
49
4
243
8
4 .‫) א‬62
:‫משוואות מעריכיות‬
:)‫פתור את המשוואות הבאות (שימוש בחוקי החזקות היסודיים‬
25  5x
2
x
 5x )12
4x  2x1 )13
2
3x
10 x 10
6
2
36 x1

x x
3
 3 )14
 100 )15
3 
x 3x
3x
)16

27
3
2 x  32
)1
32 x  27
)2
5x  25x1  625
)3
4 
8
)4
3x  81x2  92 x1
)5
100x  10000 x1 )7
5
2x
 1 )8
 27   9
4
x
125
x2  4

1

)11
25
x3 3
2  8
x2
4
)9
x
 2 )11
x1 2
32
x
5
3
4
x
1
2
)6
:)‫פתור את המשוואות הבאות (הבסיס הוא שבר‬
3
8 
2
2
4 
7
 3
27  
5
2 x 1
2 x2 9 x
5
49  
7
x 1
2
 
3
7
 
2
5
 
 3
3 x2  x
x2
 27 )25
3 x
x 8
 49 )26
 125 )27
46 x
 25 )28
2 x  43 x  1

  )22
83 x 2  2 x 4 
4
3x
4
2
)23
  
25
5
3
27  
2
49
3x 
)21
2
2 x 7
7
 
5
3
1
16   23 x 5  8x 5    
4
4 x1
 8 )24
1
)17
27
x
1
x
   4  8 )18
2
1
27   
9
x 2
x
8
1
 
x
32  2 
)19
4 x 1
)21
m
.) n a m  a n :‫ (תזכורת‬:)‫פתור את המשוואות הבאות (שימוש בחוקי שורשים‬
x 1
5x  25 )41
3
8x   2  32 x   5 1024 )35
27  x 81  3x )42
5
100  10 x
x
2
3
 10, 000 )43
x
 1 
9     x 3 )44
 27 
32  2 x
x
1
)45

8
4 x
2
1 
 
9 
   125 )31
5x
2x
)36
256 
4  8x
3
22 x 1  4 x  64  256 )31
x
3  5 27 x  1 )37
102 x 1  1000  3 10 x )38
81 3  27
8
4
 1 )46
x
8
2 x
3x 2  81 )29
x
54 x 3 
4
x9
)39
9
27

x
 3x 2 
125  5x 1
25x

1
)32
9
5
3 x
5
)33
x
25x 2
)41  1   7  343x  7 x )34
125
 49 
:)‫פתור את המשוואות הבאות (מכפלת בסיסים שונים‬
3x2  20  405  2 x )51
2x  5x  1000 )47
 7 106 )54
5  3x4  2187  5x2 )51
4  3x  2x  144 )48
3x1  2x2  5x3  0.02 )55
2 x 1  3x 2  7 x  392 )52
5x 1  3x 2  125 )49
3x  2x  729 103  5 x )53
7x
x
2
1
10x
2
4
:)‫פתור את המשוואות הבאות (משוואות עם פעולות חיבור וחיסור‬
 23x1   64
2
2 x
3
2 x
25
3 x 1
3
x
1
3
 3.75 )71
1 x
3
1 2 x
5
 2178  27
10
2
 6 10  5
3
17
)64
16
5x  6  5x  875 )57
 124 )72
x2
)73
1
2
x
8x  2  3x 1  410  4 2  6 x 3 )75
3
x 1
3x  3x  18 )56
2 x 3  2 x 1 
 4 )71
468  6x  2x2  3x1 )74
x 1
3x2  3x2  240 )63
x 1
4
x 1
)76
3x2  3x3  54 )65
81x1  18  34 x3  245 )66
3 x2
5
 3 125  28 )67
x
22 x1  4x2  66 )68
16
x
1
2
4
2 x
50
1
2
 14 )69
2x  4  2x  80 )58
7 10x  10x  600 )59
7  3x  2  3x 
5
)61
27
8x  8x2  1040 )61
2 x  2 x5  1056 )62
:)‫פתור את המשוואות הבאות (משוואות עם פעולות חיבור וחיסור‬
7x
8
 x
 3 )91
x
7 4 7 5
36 x  7  6 x  6  0 )84
2x2  2 x  8.5 )77
16x2  96  4x1  1 )85
3x  32 x  8 )78
8
77
3  x
)91
9 4
81  16
2  24 x1  3  4x  1 )86
5x  52 x  26 )79
41.5 x1  3  26 x3  56 )87
7 x4  7 x  350 )81
x
x2
x
3
6
3
 x
 x
)92
x
3  3  2 3  2 3 1
2x
2
1
 
3
25  2 x  68 5  2 x  2  82
)93

2x  2
2x  3
2
x 3
3
1
x2
2
 3 2
1
x 1
3
1
 26   
 3
 1 )88
1
x
4
22 x  7  2x  8  0 )81
9x  36  3x  243  0 )82
 3 )89
16x1  65  4x  4  0 )83
:‫פתור את מערכות המשוואות הבאות‬
x 1
y 1

2  3  17
)111

x 1
y
3

2

3

21


x 3 y

8
2
)97
 2 x7 y
3

81


 y  x 1
)94
 x
y
3  3  36
x
y

3  7  20
)111
 x
y

9  3  49  582
3 x 7 y

7
7
)98
 2 x 12 y
 256

2
x  y  3  0
)95
 x
y
2  2  2
2 x  5 y  29

)112

x
y

3  4  2  25  1298
2 x  3 y  5

)99
 x
y

2  3  1
2 x  1  y
)96

x
y2
4  3  3  15
:‫השוויונים המעריכיים הבאים‬-‫פתור את אי‬
. a x  a y  x  y :‫ אז‬0  a  1 :‫ ואם‬a x  a y  x  y :‫ אז‬a  1 :‫ אם‬:‫תזכורת‬
3x2  27 )114
2 x  16
)113
)116
16 x  8x1
)115
2 16 x  32 x  1 )118
27 x  3x  3x3
)117
0.36 x1  0.313 x )111
1
64 x     1024
2
 1 
52 x1   
 25 
x
2
2
x
51
)119
 1 
 
 32 
x 1
1
 
4
3 2 x
0.6x 1  0.6x
)112
2
81  
3
3 x 1
2 x2 3 x
2
 8 
3
 3
 
 2
1
)111
x2
x
 1 
x2

  5 )114
 625 
4
27   
9
2
1
x1
   27  3
9
2 x
 1 


 100 
)116
 5
4  

 2 
4 x
 16 )118
1
 3x 2  27 )121
9
)113
x 2 1
2 x 1
 10001 x
 25 
 5 
 16 
125  3 5x  58 x
3
)115
x
2
)117
)119
1
)122
1  42 x1  2x1  128
)121
0  25x  5x  5  625x
)124
0  8x  2x  16
)123
10 x 2
 3  9  0 )126
9
16x  4x  12  0
)125
2 x  3  24  x  2
)127
1  125  5x  5x
3
9x 
2
2
16
 2  x 6
2 x    5x )128
5
7
2 x 5
x2
 343
)129
2
)11 - 2.5 )9 2 )8 - 2 )7
3
2
- 0.5 )18 -3 )17 1 , - )16 1 , -2
3
2
1
2
, -3 )28
, -4 )27 . )26  )25
3
3
2
5
1
3.75 )38
)37 - 1.44 )36
)35
17
6
1
-40.5 )6 - 10 )5 1.75 )4 2 )3 1.5 )2 5 )1
)15 7 , -1 )14 0.5 , 1 )13  )12 1 ,
1
)11
4
2
)23 2 )22 - 4 )21 2 )21 0.8 )19
3
2
8

)34 6.5 )33 - )32 2 )31 2 )31 6 )29
9
15
- 1 )24
52
2 )48 3 )47 1 , -3 )46 -2 )45  )44 3 , -1 )43 4 , -1 )42 -2 )41 -3
2
)41 -8 )39
3
-3 )61 2 )59 4 )58 3 )57 2 )56 1 )55  2 )54 3 )53 2 )52 3 )51 2 )51 2 )49
1
1
1
1
4
)73
)72 1 )71 0 )71
)69 .1 )68 0 )67
)66 6 )65 -3 )64 3 )63 5 )62
)61
3
2
2
4
3
.2,3 )82 3 )81 -3 , -1 )81 2 , 0 )79 2 )78 1 ,  3 )77 2 )76 0 )75 2 )74

1
)91 1 )91 -4 )89 - 6 , -3 )88 1 )87 -1 )86 - 2.5 )85 -1 , 0 )84 - 2 , 1 )83
2
1,1 )99  2, 1 )98  9, 2  )97 1,1 )96  2,1 )95  2,3 )94 3 )93 1 )92
x  4 )113  2, 2  ,  4.26,1.418 )112  3,1 ,  3.182,1.318 )111  2,1 )111
x  1 , x  0.25 )118 x  3 , x  1 ) 117 x  0.25 )116 x  3 )115 x  5 )114
1
1
 x  1 )113 x  )112 x  1 , x  2 )111 x  2 )111 x  2 )119
4
9
9
1
1
1  x  )119 x  4 , x  )118 x  1.5 )117 x  1 )116
 x  1 )115
8
2
2
3
4  x  1 )123 3  x  1 , x  2 )122
 x  2 )121 4  x  1 )121
5
. x  1 , x  2 )129 x  6 )128 x  3 )127 0  x  2 )126 x  1 )125 x  1 )124
x  4 , x  0 )114 
:‫הגדרת הלוגריתם ומשוואות לוגריתמיות יסודיות‬
:‫חשב את ערכי הלוגריתמים הבאים‬
.) b  0 , a  0  1 :‫ (כאשר‬a  b  loga b  x :‫ הגדרת הלוגריתם‬:‫תזכורת‬
x
log5 5 )3
log3 81 )2
log 2 8
)1
log125 5 )6
log32 8 )5
log9 243
)4
)8
log 49 7
)7
log 1 16 )9
log32 64
2
log 1
4
1
)12
8
log 1 625 )11
25
53
log 1 27 )11
3
log 1
3
3
4
log 1
1
)15
9
3 )18
27
log
5
1
3
25
log 0.01
4
125 )21
10
)24
1000
27
)14
125
3
log 5
log 3 7
log
log 3 5 125 )16
81 )21
log 1 5 128 )19
3
5
3
9
)13
4
1
)17
343
1
27
log
log 2
8
100
)23
10
log
10
)22
1000
:‫ במשוואות הלוגריתמיות הבאות‬x ‫מצא את‬
log6 x  1 )27
log 2 x  5 )26
log3 x  2 )25
log7 x  0 )31
log 4 x  2 )29
log3 x  3 )28
1
)33
3
log 3 x  4 )32
log 1 x  2 )31
x  2  0 )36
7 log128 x  3  0 )35
log 1 x 
8
log
5
5
3
4log9 x  2  0 )34
:‫ במשוואות הלוגריתמיות הבאות‬x ‫מצא את‬
log x 25  2 )39
log x 6  1 )38
log x 3  1 )37
log x 64  3 )42
log x 625  4 )41
log x 64  2 )41
log x
1
 4 )45
81
log x
4
 2 )44
9
log x
1
 3 )43
8
:)‫פתור את המשוואות הלוגריתמיות הבאות (שימוש בהגדרת הלוגריתם‬
log5  6  7 x   3 )48
log 64  x  3 
1
)51
3
log 2  x  5  4 )47
log5  x  1  1 )46
1
)51
2
log6  3x  2   0 )49
log 4  4 x  1 
54
log0.2  2 x  1  2 )54
3
 7 x  2  2 )53
log
5
 3x  1  4 )52
2 

log3  x 2  x   3 )57
9 

log6 13x  x 2   2 )56
log 4 10 x  x 2   2 )55
log3  x  2 x 2  28  3 )61
log 2  x 2  6 x  13  3 )59
log 2  x 2  6 x  10   1 )58
log7  x 4  80   0 )63
log3  x3  44   4 )62
log 4  x3  11  2 )61
log 2
x2  5
 2 )66
x
log3
20 x  68
 2 )65
5x  2
log 4
3x  1
 1 )64
x2
log x  2 x 2  6 x  5  2 )69
log x  3x 2  5 x  3  2 )68
log x  2 x 2  9 x   2 )67
log x2  4 x  5  2 )72
log x  2 x 2  x  6   2 )71
log x  4 x 2  3x   2 )71
log
log
log
x 1
x
2
 x  2  2
8
log x    4
)74
x
)75
 4  3x  3x   2 )78
2
x2 3
log
x 3
 x  5  4 )77
log x3  3x  11  2
)73
log 4 10 x  x 2   2 )76
‫פתו ר את המשוואות הלוגריתמיות הבאות (שימוש בהגדרת הלוגריתם מספר‬
:)‫פעמים‬
2log9  log5  2 x  1   1 )81


log 1 log3  x 2  7.5 x   
1
)82
2
log 2  log3  x  3  30   5 )81
log 25  2  5x  2   x  2 )84

1 

log 2  log 0.25  x 2     1 )83
4 


16


log3  log 2 x   1 )79

log5 4  log 6 3  log 4  x 2  15  1 )86
55
 

log5 log3 log3  5 x 2  7   0 )85
:)‫פתו ר את המשוואות הלוגריתמיות הבאות (מתקבלת משוואה מעריכית‬
log3  5  2 x  1  4 )88
log 2  5x  3  7 )87
log5  5x  120   x  2 )91
log 2 12  2 x   x  1 )89
log9 10  3x  9   x )92
log 4  5  2 x1  16   x )91
log 4 17  4x   x  2 )94
log5  30  5x   x  3 )93
log 2  5  2x 1  1  2 x  4 )96
log5  49  5x  120   2 x  1 )95

x
1

log8  3  23  83 x   6 x  1 )97
3log 2 9  2 3  1  15  2 x )98
:‫פתור את המשוואות הלוגריתמיות הבאות‬
‫ והחזר את ההצבה‬t ‫ פתור משוואה עבור‬, log a x  t :‫ היעזר בהצבה של‬:‫הדרכה‬
.‫ עפ"י הגדרת הלוגריתם‬x ‫למציאת‬
 log2 x 
 log3 x 
 16
 2  log 2 x  15  0
)111
6
1
log 7 x
)112
2   log 4 x   5  log 4 x  3
)111
6
)114
12
2

3
log3 x  1 log3 x
)113
log16 x  log16 x  2  2
)116
log3 x  log3 x  2
)115
2
log 7 x 
5  log 64 x  1
 log64 x 
2
2
2
 log3 x 
56
2

 log3 x 
2
 27  3
)99
)117
6
1
1
)8
)7 )6 0.6 )5 2.5 )4 1 )3 4 )2 3 )1
5
2
3
8
7
1
-2.5 )22 -0.9 )21  )21  )19  )18 -9 )17 .9 )16 6 )15 - 3 )14 -2 )13
9
15
12
81
1
1
1
0.5 )33
)32 9 )31 1 )31 . )29
)28 6 )27 32 )26 9 )25  )24 - 0.1 )23
625
16
27
8
1
1
1
)45 1.5 )44
)43 4 )42 5 )41 8 )41 5 )39
)38 3 )37 0.2 )36 8 )35 3 )34
3
2
6
1
4,9 )56 2,8 )55 12 )54
)53 8 )52 1 )51 0.25 )51 1 )49 -17 )48 11 )47 4 )46
7
1
1 1
- 1,5 )66 2 )65 -9 )64 3 )63 5 )62 3 )61 1,  )61 1,5 )59 4,2 )58 ,  )57
2
3 9
.-1 )77 8,2 )76 3 )75 2 )74 5 )73 1 )72 2 )71  )71 5 )69 1.5 )68 9 )67
1.5 )12 - 2 )11 -3 )11 -4 )9
7 )86 2 )85 -2 )84 
1
1
)83 - 6,13.5 )82 6 )81 63 )81 8 )79 1,  )78
2
2
-3,-1 )96 0.974 ,1 )95 2,0 )94 1,2 )93 2,0 )92 1,3 )91 1 )91 2 )89 4 )88 3 )87
3
3,9 )113
1
1
1
1
1
,343 )112 , 64 )111
,8 )111
,81 )99 -12,- 3 )98  )97
49
2
3
32
81
1
. , 27 )117 2 )116 3 )115 4,8 )114
27
57
:‫חוקי הלוגריתמים ומשוואות לוגריתמיות‬
:‫תזכורת – חוקי הלוגריתמים‬
log a x  log a y  log a  x  y 
log a x  log a y  log a
x
y
log a  x   n  log a x
n
log 2 10  log 2 6.4
)3
log8 4  log8 16
)2
log3 6  log3 1.5
)1
log 2 768  log 2 6
)6
log 4 192  log 4 3
)5
log5 150  log5 6
)4
log0.25 80  log0.25 5
)9
log0.2 2  log0.2 10
3log3 6  log3 3.375 )12
)8 log81 120  log81 40 )7
log 4 1.6  2log 4 10 )11
2log6 2  log6 9 )11
log 4 24  log 4 5  log 4 10  log 4 3 )14
log3 18  log3 6  log3 4 )13
log6 10  log6 5  log6 288  log 6 4 )16
log5 50  log5 20  log5 2  log 5 4 )15

1
5
1
 log 1  log 1 2   log 1 10  log 1 8 )18
2 5 2
3 5
5 
5
1
log 3 25  2log 3 2  log 3 60 )17
2
1
 log 7 81  2log 7 6  log 7 84 )21
4
1
1
3
log 3 2 6  log 3 2 3  log 3 2 4 )19
2
2
2
k  log a a k :‫ הפוך את המספרים השלמים לביטוי לוגריתמי לפי‬:‫טיפ‬
.‫וחבר אותם לביטויים הנוספים לפי חוקי הלוגריתמים‬
. 3  log2 2  log 2 8 :2 ‫ לביטוי לוגריתמי על בסיס של‬3 ‫ נהפוך את‬:‫דוגמא‬
3
log 7 4  log 7 8
)23
log 7 2
log 4 125
)22
log 4 5
log 3 16
)21
log 3 8
log 7 5  log 7 3  4
)26
log 7 225  log 2 256
log 2 5  log 2 2  1
)25
log 2 200  3
log3 6  2
)24
log3 108  log3 2
log 4 18  log 4 2  log 4 36
)28
2log 4 6  3log 4 8  4
2  3log 5  log 50
)27
1  log128  5log 2
2  2log3 4  log3 8 89
4  log3 0.01  2log3 18
)29
58
:)10 ‫חשב את ערכי הביטויים הבאים (הלוגריתם לפי בסיס‬
log 8
)32
log 8
log 8
)31
log16
log 36  0.5log 6
)35
log12  log 2
log 72  log 8
)34
log 27
log 27
)31
log 9
log 24  log 3
)33
log 2
1  log 5
)36
log 2  2 log 5
:)10 ‫) הוכח את נכונות השוויוניים הבאים (לפי בסיס‬37
log125  1  log 2
1
log 5  1  log 2
2  log 25  2log8
6
log 3 16
log 9  2log 5  log 4
2
log10  log 2  log 6
.‫א‬
.‫ב‬
.‫ג‬
:)‫פתור את המשוואות הבאות (איחוד ביטויים באמצעות חוקי הלוגריתמים‬
log15 x  log15  x  2   1 )39
log 4 x  log 4  x  6   2 )38
log35  x  8  log35  x  6   1 )41
log 2 x  log 2  x  3  2 )41
log3  x  105  log3  x  1  3 )43
log 2  x  14   log 2 x  3 )42
log 2  2 x  8  2  log 2  5  x  )45
log 2  3x  4   log 2  x  2   1 )44
log 2 11x  4   log 2  2 x  1  log 2  2 x  3 )47
log3  x 2  11  1  log3  2 x  1 )46
log5  30 x  9   log5  4 x  5  log5  3x  2  )48
2log5  x  1  log5  2 x  3.5  log5 x )49
log 2  x  4   log 2  x  2   log 2  x  3  3 )51
log 7 12 x  35
 1 )51
2 log 7 x
59
:)‫פתור את המשוואות הבאות (שימוש בהגדרת הלוגריתם וקבלת משוואה מעריכית‬
log 2  5x  19   3  log 2 8  5x  )53
log3  2x  2   log3  2 x  14   2 )52
log3  25x  8  2  x log3 5 )55
1   x  2  log3 2  log3  4 x  32  )54
x log 2 4  log 2  2x  28  x  3 )57
log3  9x3  1  x  5  log3  3x3  1 )56
:)‫פתור את המשוואות הבאות (פתיחה באמצעות חוקי הלוגריתמים‬
log 4 16 x   log 4  64 x   12 )59
log3 x  log3  3x   6 )58
x
 2 )61
8
log 2  32 x   log 2 128x   48 )61
16
 log 4  4 x  )63
x
 27 
log3    log3 81x   10 )62
 x 
 log3 3x2  1 )65
 16 
log 2 x 2  log 2 8 x   log 2   )64
 x
log 2 x  log 2
log 4 x 2  log 4
 log3 3x 
2
 81 
log3  27 x3   log3  3x 2   log3    3 )67
 x
 log5 25x 
2
 log5 25 x 2  1 )66
 x3 
 x 
 125 
2log5 x  log5  2   2 )69 log 2    log 2  32 x 2   log 2 
  2 )68
 x 
 128 
 2
 343 
log 7  2 
 x   1  0 )71
2
 log 7 x  4
 125 
log5 x 2  log5  2   2 )71
 x 
:‫תרגילי הבעה – חוקי הלוגריתמים‬
:‫ את הביטויים הבאים‬a ‫ הבע באמצעות‬. log 2 7  a :‫) נתון‬72
log 2 14 .‫א‬
log 2 49 .‫ב‬
:‫ את הביטויים הבאים‬a ‫ הבע באמצעות‬. log3 5  a :‫) נתון‬73
log3 125 .‫א‬
log3 0.2 .‫ב‬
60
‫‪ )74‬נתון‪ . log 24 6  a :‬הבע באמצעות ‪ a‬את הביטויים הבאים‪:‬‬
‫א‪log 24 2 .‬‬
‫ב‪log 24 3 .‬‬
‫‪ )75‬נתון‪ . log 4  a :‬הבע באמצעות ‪ a‬את הביטויים הבאים‪:‬‬
‫א‪log16 .‬‬
‫ב‪log 2 .‬‬
‫ג‪log8 .‬‬
‫‪ )76‬נתון‪ . log3 5  b , log3 6  a :‬הבע באמצעות ‪ a‬ו‪ b -‬את הביטויים הבאים‪:‬‬
‫א‪log3 30 .‬‬
‫ב‪log3 1.2 .‬‬
‫ג‪log3 150 .‬‬
‫א‪log 4 0.12 .‬‬
‫ב‪log 4 2.4 .‬‬
‫א‪log 7 40 .‬‬
‫ב‪log7 320 .‬‬
‫א‪log5 6 .‬‬
‫ב‪.‬‬
‫‪log5 3 72‬‬
‫א‪.‬‬
‫‪log8 0.03‬‬
‫ב‪.‬‬
‫‪10‬‬
‫‪27‬‬
‫‪5‬‬
‫‪log8‬‬
‫א‪.‬‬
‫‪64‬‬
‫‪343‬‬
‫‪log 3‬‬
‫‪49‬‬
‫ב‪.‬‬
‫‪512‬‬
‫‪. log3 4‬‬
‫‪61‬‬
: alog b  b :‫חשב את ערכי הביטויים הבאים באמצעות הנוסחה‬
a
3
1
 
7
3
log
22log2 3 )86
10log 2 )85
0.24log0.24 6 )84
5log5 12 )83
2log2 3 )82
32log2 3 )91
8log2 3 )91
27log3 2 )89
9log3 4 )88
33log3 4 )87
5
49
log5 64
)96
81
5
1
8
log
log 2 243
9
)111  
3
3log
2
8
5
)116
)95
3
log3 16
)94
log36 4
)93
125 log5 3 )92
64log2 5 )98
3log9 2 )97
32log3 6 )113
51log5 2 )112
6
4
)111
5log125 8 )99
271log3 2 )115
4
log 4 9
2
)114
1 )14 3 )13 6 )12 2 )11 2 )11 - 2 )9 1 )8
0.5 )25 1 )24 5 )23 3 )22
1
)7 7 )6 3 )5 2 )4 6 )3 2 )2 2 )1
4
4
)21 - 2 )21 10.5 )19 -1.5 )18 - 2 )17 -2 )16 3 )15
3
4
)34 .3 )33 .2 )32 .0.75 )31 1.5 )31 0.5 )29 2 )28 1 )27 0.5 )26
3
-0.25 ,1 )47 2,4 )46 2 )45  )44 3 )43 2 )42 13 )41 4 )41 5 )39 8 )38
.1 )36 .2.5 )35
. )56 0,1.292 )55 2,3 )54 1 )53 4 )52 5,7 )51 8 )51 0.5 )49
2,
1
1
)64 2 )63 )62
16
9
1 1
,
)48
3 4
1
1
1
4 , 6 )59 9 ,
)58 2 )57
13 )61
2
4
27
1
1
1
, 3 )65
)68 )67 0.2 )66
5 )69 1 ,
4
9
3
2,4 )61 2 ,
49 , 76 )71 5 ,  5 )71
3a  1
1 a
.‫ב‬
.‫) א‬74 a .‫ ב‬3a .‫) א‬73 2a .‫ ב‬a  1 .‫) א‬72
2
2
2a  b .‫ ב‬a  b .‫) א‬78 a  1  b .‫ ב‬a  2b .‫) א‬77 a  2b .‫ ג‬a  b .‫ ב‬a  b .‫) א‬76
2a  3b
a  3b
b  2a
2
ab
3 )82
.‫ ב‬2b  3a .‫) א‬81
.‫ב‬
.‫) א‬81 b  a .‫ב‬
.‫) א‬79
4
5
2
3
2
1
)92 243 )91 27 )91 8 )89 16 )88 64 )87 9 )86 2 )85 6 )84 12 )83
27
1
2 )97 4 )96 27 )95 4 )94 4 4 )93
)111 0.25 )111 2 )99 56 )98
81
2
216 )115 3 )114 1.5 )113 10 )112
.9
)116
25
1.5a .‫ ג‬0.5a .‫ ב‬2a .‫) א‬75
62
:‫מעבר מבסיס לבסיס ומשוואות לוגריתמיות‬
:‫חשב ללא מחשבון את ערכי הביטויים הבאים‬
. a, m  0  1 , b  0 , log a b 
log m b
:‫תזכורת‬
log m a
log 2 5  log 25 4 )2
log3 6  log6 3 )1
log0.1 5  log 25 100 )4
log 27 4  log 2 3 )3
log5 8  log7 25  log 2 49 )6
log 3 7  log
log81 49  log32 3  log7 2 )8
log 4 169  log9 64  log13 243 )7
343
9 )5
:‫הוכח את השוויוניים שלפניך‬
1
log 6  log 2 6  3 )11
8
log 7 25  log5 7  2 )9
log3 8  log5 3  log 2 5  3 )12
log 4 25  log5 4  2 )11
log16 3  log5 4  log3 25  1 )14
log3 5  log5 8  log3 2  log 2 5  log3 40 )13
log a b  logc a  logb a  logc b  log c ab )16
log 2 25  log5 9  log81 2  1 )15
:‫פתור את המשוואות הבאות‬
log81 x  log3 x  5 )18
log 2 x  log8 x  4 )17
log3 x  3log 27 x 2  3 )21
5log5 x  log 1 x  11 )19
log5 x  log125 x  3 )22
log 2 x  4log16 x  8 )21
 x 7
log3  81x   log 27    )24
9 3
log 2 8x   log16 x  7 )23
log x 2  log 2 x  2 )26
 4
log 2  32 x 2   log8  3   12 )25
x 
4  log x 5  3  2  log 25 x )28
log x 3  6log 27 x  1 )27
log6 16 x  3  log x 5 6  2 )31
log3  6  x   log x 3  2 )29
25
3
63
‫‪log5 x  4.5  log5 x 125 )31‬‬
‫‪log 2  4 x   log8 x 4  3.5 )32‬‬
‫‪log x 4  3log 4 x 16  4 )33‬‬
‫‪1 4‬‬
‫‪log x  27 x   log81x     0 )34‬‬
‫‪3 5‬‬
‫‪2log 4 x 8  log x 16 x   9 )35‬‬
‫‪ 6 x   log36 x  4 )36‬‬
‫‪2‬‬
‫‪5 )37‬‬
‫‪25 x‬‬
‫‪  2  log‬‬
‫‪2‬‬
‫‪log x 5  log5 x  5 x‬‬
‫תרגילי הבעה – נוסחת המעבר בין בסיסים‪:‬‬
‫‪ )38‬נתון‪ . log 2 5  a :‬הבע באמצעות ‪ a‬את ערכי הביטויים הבאים‪:‬‬
‫א‪.‬‬
‫‪log5 2‬‬
‫ב‪.‬‬
‫‪log 4 5‬‬
‫ג‪.‬‬
‫‪log16 5‬‬
‫‪ )39‬נתון‪ . log 4 6  a :‬הבע באמצעות ‪ a‬את ערכי הביטויים הבאים‪:‬‬
‫א‪.‬‬
‫‪log 2 3‬‬
‫ב‪.‬‬
‫‪log32 36‬‬
‫ג‪.‬‬
‫‪log 216 96‬‬
‫א‪.‬‬
‫‪log3 15‬‬
‫ב‪.‬‬
‫‪log15 3‬‬
‫ג‪.‬‬
‫‪log9 25‬‬
‫‪ )41‬נתון‪ . log 2  a :‬הבע באמצעות ‪ a‬את ערכי הביטויים הבאים‪:‬‬
‫א‪log80 .‬‬
‫ב‪.‬‬
‫‪log8 40‬‬
‫ג‪.‬‬
‫‪log80 2000‬‬
‫‪64‬‬
‫‪x‬‬
‫‪3  log‬‬
‫א‪.‬‬
‫‪log36 30‬‬
‫ב‪.‬‬
‫‪log 216 180‬‬
‫ג‪.‬‬
‫‪log 1 125‬‬
‫‪6‬‬
‫‪ )43‬נתון‪ . log 2  0.3 :‬חשב את ערכי הביטויים הבאים‪:‬‬
‫א‪log 2 100 .‬‬
‫ב‪.‬‬
‫‪log8 40‬‬
‫ג‪.‬‬
‫‪log 1 5‬‬
‫‪4‬‬
‫‪)44‬‬
‫‪1‬‬
‫א‪ .‬הוכח כי לכל ‪ a, b  0  1‬מתקיימת הטענה הבאה‪:‬‬
‫‪logb a‬‬
‫‪b‬‬
‫ב‪ .‬נתון‪ . log a 5  b :‬הוכח כי מתקיים‪:‬‬
‫‪logb 5‬‬
‫‪. log a b ‬‬
‫‪. log a b ‬‬
‫ג‪ .‬נתון‪. 2  log3 a  log(bc ) 3  1 :‬‬
‫הוכח כי לכל‪ a, b, c  0  1 :‬מתקיים‪. a2  b  c :‬‬
‫פתור את המשוואות הבאות (הוצאת לוג משני אגפים)‪:‬‬
‫‪xlog2 x  16 )45‬‬
‫‪xlog3 x  3 )46‬‬
‫‪x1log3 x  729 )47‬‬
‫‪x3log5 x2  5 )48‬‬
‫‪x2log3 x8  81x )49‬‬
‫‪x‬‬
‫‪)51‬‬
‫‪8‬‬
‫‪x93log2 x ‬‬
‫תשובות סופיות ‪:‬‬
‫‪2‬‬
‫‪2‬‬
‫‪)5 - 1 )4‬‬
‫‪)3 1 )2 1 )1‬‬
‫‪3‬‬
‫‪3‬‬
‫‪1‬‬
‫‪1‬‬
‫‪1‬‬
‫‪1‬‬
‫‪, 3 )27 2 )26 0.07 ,4 )25‬‬
‫‪, 27 )24‬‬
‫‪, 16 )23‬‬
‫‪, 125 )22 4 )21‬‬
‫‪3‬‬
‫‪243‬‬
‫‪128‬‬
‫‪125‬‬
‫‪1‬‬
‫‪1‬‬
‫‪1‬‬
‫‪, 5 )28‬‬
‫‪, 2 )32‬‬
‫‪, 55 )31 0.2 ,3 )31 2 )29‬‬
‫‪.3 )34 4 )33‬‬
‫‪625‬‬
‫‪4 2‬‬
‫‪5 5‬‬
‫‪3 )21 25 )19 81 )18 8 )17 0.1 )8 15 )7 12 )6 2‬‬
‫‪65‬‬
a2
a
a
1
.‫ ג‬0.8a .‫ ב‬2a  1 .‫) א‬39
.‫ ג‬.‫ ב‬.‫) א‬38
3a
4
2
a
1
1
1
, 66 )36
)
37
, 4 )35
3
3
36
25
128
1.5
2a  1
a 1
a3
2a  1
1

.‫ג‬
.‫ב‬
.‫) א‬42
.‫ג‬
.‫ ב‬3a  1 .‫) א‬41 a .‫ג‬
.‫ ב‬a  1 .‫) א‬41
a
3a
2a
3a
a 1
3a  1
1
1
1
1
1
7
1
3,
)49 3 5 , )48 9 ,
)47 3 , )46 0.25 ,4 )45 . 1 .‫ ג‬1 .‫ ב‬13 .‫) א‬43
81
5
27
3
3
6
9
1
. 8 , 3 )51
2
:‫שוויוניים לוגריתמיים‬-‫אי‬
log5  x  2   1 )2
:‫השוויוניים הבאים‬-‫פתור את אי‬
log 4  x  3  0 )1
log  x  4   log 10  2 x  )4
log 1  x 2  3  log 1  x  5 )6
3
3
log0.5  3  x   2 )3
log 2  x  2  log 2  2 x  3 )5
log 2  x 2  3x   2  0 )8
log 4
x3 1
 )11
x2 2
log 24 x  3log 4 x  2  0 )12
1 

log 1  x 2  x   1 )7
2 
2 
9

log 2  x 2    0 )9
16 

log 2
x 5
 1 )11
x2
1  x  2 )6 x  5 )5 2  x  5 )4 x  1 )3
2  x  7 )2 3  x  4 )1
5
3 3
5
1
1
  x   ,  x  )9 x  1 , x  4 )8   x  0 ,  x  1 )7
4
4 4
4
2
2
. 0  x  4 , x  16 )12 9  x  2 )11 2  x  7 )11
66
‫פרק ‪ – 4‬גאומטריה אוקלידית‪:‬‬
‫רקע‪ ,‬קווים וזוויות‪ ,‬משולשים‪:‬‬
‫שאלות‪:‬‬
‫‪ )1‬נתון‪, CAB  DAC :‬‬
‫‪O‬‬
‫‪O‬‬
‫‪. EAB  80 , FAD  60‬‬
‫חשב את הזויות הבאות‪:‬‬
‫‪FAE  2  EAD‬‬
‫‪. FAB , EAC , CAB‬‬
‫‪ )2‬חשב את סכום הזויות הבאות (נמק)‪:‬‬
‫‪. 2 4 6‬‬
‫‪ )3‬מצא את זוגות הישרים המקבילים‬
‫בשרטוט הבא (נמק)‪.‬‬
‫‪FAB  120 , EAC  50 , CAB  30 )1‬‬
‫‪. d c , a c , e f )3 180 )2‬‬
‫משולש כללי‪ ,‬משולש שווה שוקיים‪ ,‬משולש ישר זווית‪:‬‬
‫משפטים כלליים במשולשים‪:‬‬
‫‪ .1‬סכום הזוויות במשולש הוא ‪.180O‬‬
‫‪ .2‬סכום שתי צלעות במשולש גדול מהצלע השלישית‪.‬‬
‫‪ .3‬במשולש מול הזווית הגדולה נמצאת הצלע הגדולה ולהפך‪.‬‬
‫במשולש מול הזווית הקטנה נמצאת הצלע הקטנה ולהפך‪.‬‬
‫במשולש מול זוויות שוות נמצאות צלעות שוות ולהפך‪.‬‬
‫‪67‬‬
‫משפטים במשולש שווה שוקיים‪:‬‬
‫‪ .1‬במשולש שווה שוקיים זוויות הבסיס שוות זו לזו‪.‬‬
‫(משפט הפוך) משולש שבו שתי זוויות שוות הוא משולש שווה שוקיים‪.‬‬
‫‪ .2‬במשולש שווה שוקיים חוצה זווית הראש‪ ,‬הגובה לבסיס והתיכון לבסיס מתלכדים‪.‬‬
‫(משפט הפוך) משולש שבו חוצה זווית הוא גם גובה או חוצה זווית הוא גם‬
‫תיכון או גובה הוא גם תיכון הוא משולש שווה שוקיים‪.‬‬
‫משפטים במשולש שווה צלעות‪:‬‬
‫הגדרה‪ :‬משולש שבו כל הצלעות שוות הוא משולש שווה צלעות‪.‬‬
‫‪ .1‬במשולש שווה צלעות כל הזוויות שוות ‪. 60‬‬
‫‪( .2‬משפט הפוך) משולש שבו כל הזוויות שוות הוא משולש שווה צלעות‪.‬‬
‫‪A‬‬
‫‪ )4‬המשולש ‪ ABC‬שבציור הוא משולש שווה שוקיים )‪.(AB=AC‬‬
‫‪ AG‬חוצה את זווית ‪. A‬‬
‫‪ M‬היא נקודה כלשהי על ‪.AG‬‬
‫הוכח כי‪.BM = CM :‬‬
‫‪C‬‬
‫‪ )5‬המשולש ‪ ABC‬שבציור הוא משולש שווה שוקיים )‪.(AB=AC‬‬
‫ו‪ BP-‬חוצים את הזוויות ‪ A‬ו‪ ABC -‬בהתאמה‪.‬‬
‫הנקודה ‪ Q‬נמצאת על המשך ‪.AG‬‬
‫‪P‬‬
‫נתון‪.GM = GQ :‬‬
‫הוכח‪. B1  B3 :‬‬
‫‪C‬‬
‫‪M‬‬
‫‪G‬‬
‫‪A‬‬
‫‪M‬‬
‫‪1‬‬
‫‪2‬‬
‫‪G‬‬
‫‪Q‬‬
‫‪68‬‬
‫‪B‬‬
‫‪3‬‬
‫‪B‬‬
‫חפיפת משולשים‪:‬‬
‫הגדרה‪:‬‬
‫משולשים חופפים הם משולשים ששווים זה לזה בכל צלעותיהם ובכל זוויותיהם‬
‫בהתאמה‪.‬‬
‫‪D‬‬
‫‪ AB  DE , AC  DF , BC  EF‬‬
‫‪ABC  DEF  ‬‬
‫‪ A D, B E, C  F‬‬
‫‪A‬‬
‫‪F‬‬
‫‪E‬‬
‫‪C‬‬
‫‪B‬‬
‫משפטי החפיפה‪:‬‬
‫‪ .1‬משפט חפיפה צלע‪-‬זווית‪ -‬צלע (צ‪.‬ז‪.‬צ)‪ :‬אם בין שני משולשים שוות שתי צלעות‬
‫והזווית שביניהן בהתאמה אז המשולשים חופפים‪.‬‬
‫‪ .2‬משפט חפיפה זווית‪-‬צלע‪ -‬זווית (ז‪.‬צ‪.‬ז)‪ :‬אם בין שני משולשים שוות שתי זוויות‬
‫והצלע שביניהן בהתאמה אז המשולשים חופפים‪.‬‬
‫‪ .3‬משפט חפיפה צלע‪-‬צלע‪-‬צלע (צ ‪.‬צ‪.‬צ)‪ :‬אם בין שני משולשים שוות שלוש צלעות‬
‫בהתאמה אז המשולשים חופפים‪.‬‬
‫‪ .4‬משפט חפיפה צלע‪-‬צלע‪ -‬והזווית הגדולה (צ‪.‬צ‪.‬ז)‪ :‬אם בין שני משולשים שוות שתי‬
‫צלעות והזווית שמול הצלע הגדולה מביניהן בהתאמה אז המשולשים חופפים‪.‬‬
‫‪A‬‬
‫‪ )6‬בציור נתון‪. AC  EC , DC  BC :‬‬
‫הוכח‪:‬‬
‫א‪. CDE  CBA .‬‬
‫ב‪. ADE  ABE .‬‬
‫‪D‬‬
‫‪C‬‬
‫‪ )7‬בציור נתון‪. DBC  ACB , ABC  DCB :‬‬
‫הוכח‪. AB  DC :‬‬
‫‪E‬‬
‫‪B‬‬
‫‪A‬‬
‫‪D‬‬
‫‪E‬‬
‫‪C‬‬
‫‪B‬‬
‫‪A‬‬
‫‪ )8‬בציור נתון‪. AC  DE , AB  BE  AD :‬‬
‫הוכח‪ :‬הנקודה ‪ D‬היא אמצע הצלע ‪. BC‬‬
‫‪C‬‬
‫‪B‬‬
‫‪D‬‬
‫‪69‬‬
‫‪E‬‬
‫זווית חיצונית למשולש ומשולש ישר זווית‪:‬‬
‫זווית חיצונית למשולש‪:‬‬
‫זווית חיצונית למשולש היא זווית הכלואה בין צלע‬
‫במשולש להמשך צלע הסמוכה לה‪.‬‬
‫משפט‪ :‬זווית חיצונית למשולש שווה לסכום שתי הזוויות הפנימיות שאינן צמודות לה‪.‬‬
‫משפטים במשולש ישר זווית‪:‬‬
‫‪ .1‬סכום הזוויות החדות במשולש ישר זווית הוא ‪. 90‬‬
‫‪ .2‬במשולש שזוויותיו ‪ , 30 , 60 , 90‬הניצב שמול הזווית של ה‪ 30 -‬שווה למחצית היתר‪.‬‬
‫‪( .3‬משפט הפוך ל‪ ) 2-‬אם במשולש ישר זווית אחד הניצבים שווה למחצית היתר‪,‬‬
‫אז הזווית שמול ניצב זה היא בת ‪. 30‬‬
‫‪ .4‬במשולש ישר זווית התיכון ליתר שווה למחצית היתר‪.‬‬
‫‪( .5‬משפט הפוך ל‪ :) 4-‬אם במשולש תיכון שווה למחצית הצלע אותה הוא חוצה‪,‬‬
‫אז המשולש ישר זווית (כאשר הזווית ממנה יוצא התיכון היא הזווית הישרה)‪.‬‬
‫‪ .6‬משפט פיתגורס‪ :‬במשולש ישר זווית סכום ריבועי הניצבים שווה לריבוע היתר‪.‬‬
‫כלומר‪(2 :‬יתר) = ‪(2‬ניצב) ‪(2 +‬ניצב)‪.‬‬
‫‪( .7‬משפט הפוך למשפט פיתגורס) אם במשולש סכום ריבועי שתי צלעות שווה‬
‫לריבוע הצלע השלישית‪ ,‬אז המשולש ישר זווית‪.‬‬
‫‪ )9‬הוכח את המשפט‪" :‬זווית חיצונית למשולש שווה לסכום שתי הזוויות‬
‫הפנימיות שאינן צמודות לה"‪.‬‬
‫‪A‬‬
‫‪ )11‬המשולש ‪ ABC‬שבציור הוא משולש שווה צלעות‪.‬‬
‫נתון‪.AN = BM :‬‬
‫הוכח‪. NQC  60o :‬‬
‫‪N‬‬
‫‪Q‬‬
‫‪M‬‬
‫‪70‬‬
‫‪C‬‬
‫‪B‬‬
‫‪ )11‬המשולש ‪ ABC‬שבציור הוא משולש שווה שוקיים )‪.(AB = AC‬‬
‫נתון‪ 18 , ABD  30o , DAC  90o :‬ס"מ = ‪.BC‬‬
‫חשב את אורכו של הקטע ‪.BD‬‬
‫‪A‬‬
‫‪C‬‬
‫‪B‬‬
‫‪D‬‬
‫‪ )12‬המשולש ‪ ABC‬שבציור הוא משולש ישר זווית ( ‪.) ABC  90o‬‬
‫‪ BQ‬הוא הגובה ליתר ‪ AC‬ו‪ BP-‬הוא התיכון ליתר ‪.AC‬‬
‫‪B‬‬
‫נתון‪. BQ  12 BP :‬‬
‫חשב את גודלה של הזווית ‪. C‬‬
‫‪Q C‬‬
‫‪A‬‬
‫‪P‬‬
‫‪ )13‬המשולש ‪ BDC‬שבציור הוא משולש שווה שוקיים )‪.(BD=DC‬‬
‫‪B‬‬
‫‪ AC‬חוצה את הזווית ‪ . BAE‬נתון‪. DC AE :‬‬
‫חשב את גודלה של הזווית ‪. ACB‬‬
‫‪C‬‬
‫‪D‬‬
‫‪E‬‬
‫‪ AD )14‬הוא גובה במשולש ‪.ABC‬‬
‫נתון‪. BC  25cm , AC  20cm , AB  15cm :‬‬
‫‪A‬‬
‫‪A‬‬
‫א‪ .‬מצא את אורכו של ‪ AD‬ואת שטח המשולש ‪.ABC‬‬
‫ב‪ .‬האם המשולש ‪ ABC‬ישר זווית? נמק‪.‬‬
‫‪C‬‬
‫‪ )15‬המשולש ‪ ABC‬הוא שווה שוקיים ‪.  AB  AC ‬‬
‫על השוק ‪ AC‬ועל הבסיס ‪ BC‬בונים משולשים שווי‬
‫צלעות ‪ ACE‬ו‪.BCD-‬‬
‫מחברים את הנקודה ‪ D‬עם הקדקודים ‪ A‬ו‪.E-‬‬
‫א‪ .‬הוכח‪. ABD  ACD :‬‬
‫ב‪ .‬ידוע גם כי‪. DE BC :‬‬
‫הוכח‪. ADE  90 :‬‬
‫‪71‬‬
‫‪D‬‬
‫‪B‬‬
‫‪C  75 )12 BD  6cm )11‬‬
‫‪ACB  90 )13‬‬
‫‪ )14‬א‪ SABC  150cm , AD  12cm .‬ב‪ .‬כן‪.‬‬
‫‪2‬‬
‫קטעים מיוחדים במשולש‪:‬‬
‫קטע אמצעים במשולש‪:‬‬
‫הגדרה‪ :‬קטע המחבר אמצעי שתי צלעות במשולש נקרא קטע אמצעים במשולש‪.‬‬
‫‪ .1‬קטע אמצעים במשולש מקביל לצלע השלישית ושווה למחציתה‪.‬‬
‫‪( .2‬משפט הפוך ‪ :) 1‬קטע היוצא מאמצע צלע במשולש ומקביל לצלע השלישית‬
‫חוצה את הצלע השנייה (כלומר הוא קטע אמצעים במשולש)‪.‬‬
‫‪( .3‬משפט הפוך ‪ :) 2‬קטע המחבר שתי צלעות במשולש‪ ,‬מקביל לצלע השלישית‬
‫ושווה למחציתה הוא קטע אמצעים במשולש‪.‬‬
‫מפגש התיכונים במשולש‪:‬‬
‫‪ .1‬שלושת התיכונים במשולש נפגשים בנקודה אחת המחלקת כל תיכון‬
‫ביחס של ‪ 1:2‬כך שהחלק הקצר קרוב לצלע‪.‬‬
‫‪ .2‬אם נקודה מחלקת תיכון (אחד) במשולש ביחס של ‪ 1:2‬כך שהחלק הקצר קרוב‬
‫לצלע‪ ,‬נקודה זו היא מפגש התיכונים במשולש‪.‬‬
‫‪ .3‬נקודת מפגש התיכונים במשולש נקראת גם מרכז הכובד של המשולש‪.‬‬
‫‪A‬‬
‫‪ )16‬הקטע ‪ MN‬הוא קטע אמצעים במשולש ‪. ABC‬‬
‫‪ AQ‬הוא גובה לצלע ‪.BC‬‬
‫הוכח‪. N1  N2 :‬‬
‫‪ AF )17‬הוא גובה לצלע ‪ BC‬ו‪ CG -‬הוא תיכון לצלע‬
‫במשולש ‪ . ABC‬הקטע ‪ GH‬מאונך לצלע ‪. BC‬‬
‫א‪ .‬הוכח‪. BH  HF :‬‬
‫ב‪ .‬נתון בנוסף כי הגובה ‪ AF‬חוצה את‬
‫התיכון ‪ GC‬ושגודלו של ‪ AF‬הוא ‪ 12‬ס"מ‪.‬‬
‫‪P‬‬
‫‪1 N‬‬
‫‪2 3‬‬
‫‪C‬‬
‫‪M‬‬
‫‪B‬‬
‫‪Q‬‬
‫‪A‬‬
‫‪AB‬‬
‫‪G‬‬
‫‪E‬‬
‫‪C‬‬
‫‪B‬‬
‫‪H‬‬
‫‪F‬‬
‫‪A‬‬
‫חשב את אורך הקטע ‪. EF‬‬
‫‪ )18‬המשולש ‪ ABC‬שבציור הוא מש"ש ( ‪) AB  AC‬‬
‫שבו ‪ AH‬הוא הגובה לבסיס ‪ ,CD .BC‬התיכון‬
‫‪72‬‬
‫‪Q‬‬
‫‪D‬‬
‫‪M‬‬
‫‪C‬‬
‫‪H‬‬
‫‪B‬‬
‫לשוק ‪ ,AB‬יוצר זווית של ‪ 30o‬עם הבסיס ‪.BC‬‬
‫נתון‪ . DQ BC , BC  12 3 cm :‬חשב את אורך הקטע ‪.MQ‬‬
‫‪ )16‬ב‪EF  3cm .‬‬
‫‪. MQ  3cm )17‬‬
‫מרובעים‪:‬‬
‫הגדרה‪ :‬מרובע הוא מצולע בעל ‪ 4‬צלעות‪.‬‬
‫משפט‪ :‬סכום הזוויות במרובע הוא ‪. 360o‬‬
‫מקבילית‪:‬‬
‫הגדרה‪ :‬מקבילית היא מרובע שבו שני זוגות של צלעות נגדיות מקבילות‪.‬‬
‫תכונות המקבילית‪:‬‬
‫‪ .1‬במקבילית כל שתי צלעות נגדיות שוות זו לזו‪.‬‬
‫‪A‬‬
‫‪B‬‬
‫‪ .2‬במקבילית כל שתי זוויות נגדיות שוות‪.‬‬
‫‪ .3‬במקבילית סכום כל שתי זוויות סמוכות הוא ‪.180‬‬
‫‪D‬‬
‫‪C‬‬
‫‪ .4‬במקבילית האלכסונים חוצים זה את זה‪.‬‬
‫‪ .5‬היקף מקבילית ‪ ‬סכום הצלעות‪ ,‬שטח מקבילית ‪ ‬צלע ‪ ‬גובה לצלע‪.‬‬
‫כדי להוכיח כי מרובע הוא מקבילית נשתמש באחת הדרכים הבאות‪:‬‬
‫‪ .1‬מרובע שבו כל זוג צלעות נגדיות מקבילות הוא מקבילית‪.‬‬
‫‪ .2‬מרובע שבו כל זוג צלעות נגדיות שוות הוא מקבילית‪.‬‬
‫‪ .3‬מרובע שבו זוג צלעות שוות ומקבילות הוא מקבילית‪.‬‬
‫‪ .4‬מרובע שבו כל זוג זוויות נגדיות שוות הוא מקבילית‪.‬‬
‫‪ .5‬מרובע שאלכסוניו חוצים זה את זה הוא מקבילית‪.‬‬
‫מלבן‪:‬‬
‫הגדרה‪ :‬מלבן הוא מרובע שכל זוויותיו ישרות‪.‬‬
‫‪B‬‬
‫(מסקנה‪ :‬מלבן הוא סוג של מקבילית)‪.‬‬
‫‪A‬‬
‫‪73‬‬
‫‪C‬‬
‫‪D‬‬
‫תכונות המלבן (בנוסף לתכונות המקבילית)‪:‬‬
‫‪ .1‬ארבע זוויות המלבן שוות והן זוויות ישרות‪.‬‬
‫‪ .2‬האלכסונים במלבן שווים זה לזה‬
‫‪ .3‬היקף מלבן ‪ ‬סכום הצלעות‪ ,‬שטח מלבן ‪ ‬צלע ‪ ‬גובה לצלע‪.‬‬
‫כדי להוכיח כי מרובע הוא מלבן נשתמש באחת הדרכים הבאות‪:‬‬
‫‪ .1‬מרובע שבו שלוש זוויות ישרות הוא מלבן‪.‬‬
‫‪ .2‬מקבילית שבה זווית ישרה היא מלבן‪.‬‬
‫‪ .3‬מקבילית שבה האלכסונים שווים היא מלבן‪.‬‬
‫מעוין‪:‬‬
‫‪A‬‬
‫הגדרה‪ :‬מעוין הוא מרובע שכל צלעותיו שוות‪.‬‬
‫(מסקנה‪ :‬מעוין הוא סוג של מקבילית)‪.‬‬
‫תכונות המעוין (בנוסף לתכונות המקבילית)‪:‬‬
‫‪A‬‬
‫‪B‬‬
‫‪B‬‬
‫‪C‬‬
‫‪D‬‬
‫‪D‬‬
‫‪ .1‬במעוין כל הצלעות שוות‪.‬‬
‫‪C‬‬
‫‪ .2‬במעוין האלכסונים מאונכים זה לזה‪.‬‬
‫‪ .3‬במעוין האלכסונים הם חוצי זוויות‪.‬‬
‫‪ .4‬היקף מעוין ‪ ‬צלע ‪ ,4 ‬שטח מעוין ‪ ‬צלע ‪ ‬גובה לצלע ‪(/2 ‬אלכסון ‪ ‬אלכסון)‪.‬‬
‫כדי להוכיח כי מרובע הוא מעוין נשתמש באחת הדרכים הבאות‪:‬‬
‫‪ .1‬מרובע שבו כל הצלעות שוות הוא מעוין‪.‬‬
‫‪ .2‬מקבילית שבה שתי צלעות סמוכות שוות היא מעוין‪.‬‬
‫‪ .3‬מקבילית שבה האלכסונים מאונכים זה לזה היא מעוין‪.‬‬
‫‪ .4‬מקבילית שבה אלכסון חוצה זווית היא מעוין (מספיק אחד)‪.‬‬
‫‪B‬‬
‫‪A‬‬
‫ריבוע‪:‬‬
‫הגדרה‪ :‬ריבוע הוא מרובע שכל צלעותיו שוות וכל זוויותיו שוות‪.‬‬
‫(מסקנה‪ :‬ריבוע הוא סוג של מקבילית‪ ,‬סוג של מלבן וסוג של מעוין)‪.‬‬
‫‪C‬‬
‫‪74‬‬
‫‪D‬‬
‫מכאן‪ ,‬שבנוסף לתכונות שבהגדרת הריבוע מתקיים כי אלכסוני הריבוע‬
‫חוצים זה את זה‪ ,‬שווים זה לזה‪ ,‬מאונכים זה לזה וחוצים את זוויות הריבוע‪.‬‬
‫היקף ריבוע ‪ ‬צלע ‪ ,4 ‬שטח ריבוע ‪(2 ‬צלע) ‪(2/2 ‬אלכסון)‬
‫כדי להוכיח כי מרובע הוא ריבוע נשתמש באחת הדרכים הבאות‪:‬‬
‫‪ .1‬מלבן שבו האלכסונים מאונכים הוא ריבוע‪.‬‬
‫‪ .2‬מלבן שבו אלכסון חוצה זווית הוא ריבוע‪.‬‬
‫‪ .3‬מלבן שבו שתי צלעות סמוכות שוות הוא ריבוע‪.‬‬
‫‪ .4‬מעוין שבו האלכסונים שווים הוא ריבוע‪.‬‬
‫‪ .5‬מעוין שבו זווית ישרה הוא ריבוע‪.‬‬
‫טרפז‪:‬‬
‫הגדרה ‪ :‬טרפז הוא מרובע שבו זוג אחד בלבד של צלעות נגדיות מקבילות‪.‬‬
‫היקף טרפז ‪ ‬סכום הצלעות‪ ,‬שטח טרפז ‪(/2 ‬גובה ‪ ‬סכום הבסיסים)‪.‬‬
‫טרפז כללי‪:‬‬
‫טרפז ישר זווית‪:‬‬
‫טרפז שווה שוקיים‪:‬‬
‫משפטים הנוגעים לטרפז שווה שוקיים‪:‬‬
‫‪ .1‬בטרפז שווה שוקיים הזוויות שליד אותו בסיס שוות זו לזו‪.‬‬
‫‪( .2‬משפט הפוך) טרפז שבו הזוויות שליד אותו בסיס שוות זו לזו הוא טרפז שווה שוקיים‪.‬‬
‫‪ .3‬בטרפז שווה שוקיים האלכסונים שווים זה לזה‪.‬‬
‫‪( .4‬משפט הפוך) טרפז שבו האלכסונים שווים זה לזה הוא טרפז שווה שוקיים‪.‬‬
‫‪75‬‬
‫קטע אמצעים בטרפז‪:‬‬
‫הגדרה‪ :‬קטע אמצעים בטרפז הוא קטע המחבר את אמצעי השוקיים בטרפז‪.‬‬
‫‪ .1‬קטע אמצעים בטרפז מקביל לבסיסים ושווה למחצית סכומם‪.‬‬
‫‪( .2‬משפט הפוך) קטע היוצא מאמצע שוק אחת בטרפז‬
‫ומקביל לבסיסים‪ ,‬חוצה את השוק השנייה‬
‫(כלומר הוא קטע אמצעים בטרפז)‪.‬‬
‫‪A‬‬
‫דלתון‪:‬‬
‫הגדרה ‪ :‬דלתון הוא מרובע שבו שני זוגות של צלעות סמוכות שוות‪.‬‬
‫(מסקנה‪ :‬דלתון הוא מרובע שניתן לפרק לשני משולשים‬
‫שווי שוקיים בעלי בסיס משותף)‪.‬‬
‫‪B‬‬
‫‪D‬‬
‫‪C‬‬
‫תכונות האלכסונים בדלתון‪:‬‬
‫‪ .1‬האלכסון הראשי בדלתון חוצה את זוויות הראש‪ ,‬חוצה את האלכסון המשני‬
‫ומאונך לו‪.‬‬
‫‪ .2‬האלכסון הראשי אינו בהכרח גדול מהאלכסון המשני‪.‬‬
‫‪ .3‬היקף דלתון ‪ ‬סכום הצלעות‪ ,‬שטח דלתון ‪(/2 ‬אלכסון ‪ ‬אלכסון)‪.‬‬
‫משפחת המרובעים‪:‬‬
‫‪76‬‬
77
‫‪A‬‬
‫‪ )1‬המשולשים ‪ ABC‬ו‪ ACD -‬שבציור הם‬
‫משולשים שווי שוקיים ( ‪.) AB  AC  AD‬‬
‫נתון‪. BAD  80o :‬‬
‫חשב את גודלה של הזווית ‪. BCD‬‬
‫‪B‬‬
‫‪D‬‬
‫‪C‬‬
‫‪ )2‬נתונה מקבילית ‪ ABCD‬שאלכסוניה נפגשים בנקודה ‪. M‬‬
‫נתון‪. AC  20cm , BC  12 DB , DQ  AC :‬‬
‫חשב את אורך הקטע ‪. AQ‬‬
‫‪B‬‬
‫‪A‬‬
‫‪Q‬‬
‫‪M‬‬
‫‪C‬‬
‫‪D‬‬
‫‪ )3‬את הצלע ‪ AB‬במקבילית ‪ ABCD‬האריכו כאורכה עד לנקודה ‪. T‬‬
‫הוכח‪ BTCD :‬מקבילית‪.‬‬
‫‪A‬‬
‫‪B‬‬
‫‪M‬‬
‫‪ )4‬נתון מלבן ‪ ABCD‬שבו ‪. DM  MC‬‬
‫הוכח‪. MAB  MBA :‬‬
‫‪D‬‬
‫‪C‬‬
‫‪ )5‬נתונה מקבילית ‪ ABCD‬ובה ‪ CM , BQ , AP‬ו‪ DN -‬הם‬
‫חוצי הזוויות ‪ C , B , A‬ו ‪ D -‬בהתאמה‪.‬‬
‫הוכח‪ TRLS :‬מלבן‪.‬‬
‫‪ )6‬נתון מעוין ‪ ABCD‬שאלכסוניו נפגשים בנקודה ‪. M‬‬
‫האריכו את הצלע ‪ AB‬עד לנקודה ‪ E‬כך‬
‫‪B‬‬
‫שמתקיים‪. ED  DB :‬‬
‫הוכח‪. AD  AE :‬‬
‫‪A‬‬
‫‪M‬‬
‫‪C‬‬
‫‪D‬‬
‫‪ )7‬נתון מלבן ‪ ABCD‬שאלכסוניו נפגשים בנקודה ‪. M‬‬
‫האריכו את הצלע ‪ AB‬כאורכה עד לנקודה ‪ F‬ואת‬
‫‪E‬‬
‫הצלע ‪ AD‬כאורכה עד לנקודה ‪ E‬כמתואר בשרטוט‪.‬‬
‫הוכח‪ :‬המרובע ‪ EBDF‬הוא מעוין‪.‬‬
‫‪A‬‬
‫‪B‬‬
‫‪78‬‬
‫‪M‬‬
‫‪C‬‬
‫‪E‬‬
‫‪D‬‬
‫‪F‬‬
‫‪ )8‬המרובע ‪ ABCD‬הוא מקבילית שבה אורך הצלע ‪AB‬‬
‫גדולה פי ‪ 2‬מהצלע ‪ .AD‬ממשיכים את הצלע ‪ AD‬עד‬
‫לנקודה ‪ K‬ומחברים אותה לקודקוד ‪.B‬‬
‫מעבירים את הקטע ‪ FE‬כך ש ‪ F-‬היא אמצע הקטע ‪.BK‬‬
‫‪ EF‬חותך את הצלע ‪ AB‬בנקודה ‪ G‬ומקביל לצלע ‪.AD‬‬
‫א‪ .‬הוכח כי המרובע ‪ AGED‬הוא מעוין‪.‬‬
‫ב‪ .‬שטח המעוין ‪ AGED‬הוא ‪ 20‬סמ"ר‪.‬‬
‫חשב את שטח המרובע ‪DCBK‬‬
‫אם ידוע כי ‪ A‬היא אמצע הקטע ‪.DK‬‬
‫‪E‬‬
‫‪B‬‬
‫‪ )9‬בריבוע ‪ ABCD‬נתון כי ‪. AE  BF‬‬
‫הוכח‪. DE  AF :‬‬
‫‪A‬‬
‫‪M‬‬
‫‪F‬‬
‫‪D‬‬
‫‪C‬‬
‫‪A‬‬
‫‪ )11‬נתון מעוין ‪ ABCD‬שאלכסוניו נפגשים בנקודה ‪. M‬‬
‫‪E‬‬
‫‪1‬‬
‫נתון‪. EBA  15o , MB  AB , AE  FC :‬‬
‫‪2‬‬
‫הוכח‪ :‬המרובע‬
‫‪EBFD‬‬
‫‪B‬‬
‫הוא ריבוע‪.‬‬
‫‪M‬‬
‫‪D‬‬
‫‪F‬‬
‫‪C‬‬
‫‪ )11‬נתון טרפז ‪ ABCD‬שאורכי צלעותיו נתונים בשרטוט‪.‬‬
‫חשב את שטח הטרפז (פתור כתרגיל חישוב)‪.‬‬
‫‪B‬‬
‫‪5cm‬‬
‫‪A‬‬
‫‪13cm‬‬
‫‪20cm‬‬
‫‪D‬‬
‫‪C‬‬
‫‪26cm‬‬
‫‪A‬‬
‫‪B‬‬
‫‪ )12‬נתון מלבן ‪ ABCD‬שאלכסוניו נפגשים בנקודה ‪. O‬‬
‫נתון‪. MN DC :‬‬
‫הוכח‪ DMNC :‬טרפז שווה שוקיים‪.‬‬
‫‪N‬‬
‫‪O‬‬
‫‪C‬‬
‫‪79‬‬
‫‪M‬‬
‫‪D‬‬
‫‪ )13‬המרובע ‪ ABCD‬הוא טרפז ישר זווית ‪ .  A  90‬הנקודה ‪ M‬נמצאת על אמצע‬
‫האלכסון ‪ BD‬של הטרפז וממנה מעבירים את‬
‫הקטעים ‪ ME‬ו‪ MF-‬השווים זה לזה ומחברים‬
‫אותה עם הקודקוד ‪.A‬‬
‫נתון כי‪ ME  MF :‬וכי‪. DFM  90 :‬‬
‫א‪ .‬הוכח‪. AFM  MBE :‬‬
‫ב‪ .‬נתון כי‪. AE  FD  1 , BC  32 :‬‬
‫כמו כן‪. AM BC :‬‬
‫‪ .1‬מצא את אורך הקטע ‪.BE‬‬
‫‪ .2‬חשב את שטח הטרפז ‪.ABCD‬‬
‫‪ KN )14‬הוא קטע אמצעים בטרפז ישר זווית‬
‫( ‪ ) AD  AB , AB DC‬שאלכסוניו נפגשים בנקודה ‪. O‬‬
‫‪ABCD‬‬
‫‪A‬‬
‫‪B‬‬
‫‪O‬‬
‫נתון‪. AD  12cm , DC  2 AB , ADB  45O :‬‬
‫חשב את אורך הקטע ‪. LM‬‬
‫‪N‬‬
‫‪M‬‬
‫‪K‬‬
‫‪L‬‬
‫‪D‬‬
‫‪C‬‬
‫‪A‬‬
‫‪ )15‬בדלתון ‪ ABCD‬האריכו את האלכסון המשני‬
‫משני צדיו כמתואר בשרטוט כך שמתקיים‪:‬‬
‫‪. KD  BL‬‬
‫הוכח‪ :‬המרובע ‪ ALCK‬הוא דלתון‪.‬‬
‫‪L‬‬
‫‪B‬‬
‫‪M‬‬
‫‪C‬‬
‫‪BCD  140 )1‬‬
‫‪ 186 )11‬סמ"ר = ‪S‬‬
‫‪ )8 AQ  5cm )2‬ב‪ 60 .‬סמ"ר‪.‬‬
‫‪ )13‬ב‪ 3 .1 .‬ס"מ‪ 24 .2 .‬סמ"ר‪. LM  6cm )14 .‬‬
‫‪80‬‬
‫‪D‬‬
‫‪K‬‬
‫המעגל‪:‬‬
‫הגדרות‪:‬‬
‫‪ ‬מעגל – המקום הגאומטרי של כל הנקודות שמרחקן מנקודה קבועה קבוע‪.‬‬
‫הנקודה הקבועה נקראת מרכז המעגל‪.‬‬
‫‪ ‬רדיוס – קטע המחבר את מרכז המעגל עם נקודה על המעגל‪.‬‬
‫‪ ‬מיתר – קטע המחבר שתי נקודות שעל המעגל‪.‬‬
‫‪ ‬קוטר – מיתר העובר במרכז המעגל‪.‬‬
‫מרכז‬
‫המעגל‬
‫‪ ‬היקף מעגל = ‪. 2 R‬‬
‫מיתר‬
‫‪ ‬שטח מעגל = ‪.  R 2‬‬
‫‪ ‬קשת – חלק מהיקף המעגל‪.‬‬
‫‪ ‬גזרה – חלק משטח המעגל‪.‬‬
‫‪ ‬זווית מרכזית – זווית שקדקודה במרכז המעגל ושוקיה רדיוסים‪.‬‬
‫‪ ‬זווית היקפית – זווית שקדקודה על היקף המעגל ושוקיה מיתרים‪.‬‬
‫משפטים במעגל‪:‬‬
‫משפטים העוסקים במיתרים במעגל‪:‬‬
‫‪ .1‬מיתרים שווים נשענים על קשתות שוות ולהפך‪.‬‬
‫‪ .2‬על מיתרים שווים נשענות זוויות מרכזיות שוות ולהפך‪.‬‬
‫‪ .3‬מיתרים שווים נמצאים במרחקים שווים ממרכז המעגל‪.‬‬
‫‪( .4‬משפט הפוך ל‪ ) 3-‬מיתרים הנמצאים במרחק שווה ממרכז המעגל שווים‪.‬‬
‫‪ .5‬אנך למיתר ממרכז המעגל חוצה את המיתר‪.‬‬
‫‪( .6‬משפט הפוך ל‪ ))1( 5-‬רדיוס החוצה מיתר מאונך לו‪.‬‬
‫‪( .7‬משפט הפוך ל‪ )) 2( 5-‬קטע היוצא מאמצע מיתר ומאונך לו‪ ,‬עובר במרכז המעגל‪.‬‬
‫‪81‬‬
‫משפטים העוסקים בזוויות במעגל‪:‬‬
‫‪ .8‬שתי זוויות היקפיות הנשענות על אותה קשת‪/‬קשתות שוות‪ ,‬שוות ביניהן‪.‬‬
‫‪( .9‬משפט הפוך ל‪ ) 8-‬זוויות היקפיות שוות נשענות על קשתות שוות‪.‬‬
‫‪ .10‬זווית היקפית שווה למחצית הזווית המרכזית הנשענת על אותה קשת‪.‬‬
‫‪ .11‬זווית היקפית הנשענת על קוטר היא זווית ישרה‪.‬‬
‫‪( .12‬משפט הפוך ל‪ ) 11-‬מיתר עליו נשענת זווית היקפית ישרה הוא קוטר‪.‬‬
‫משפטים העוסקים במשיק למעגל ושני משיקים למעגל‪:‬‬
‫‪ .13‬משיק מאונך לרדיוס בנקודת ההשקה‪.‬‬
‫‪( .14‬משפט הפוך ל‪ )13-‬קטע המאונך לרדיוס בקצהו משיק למעגל‪.‬‬
‫‪ .15‬שני משיקים למעגל היוצאים מאותה נקודה שווים זה לזה‪.‬‬
‫‪ .16‬קטע המחבר את מרכז המעגל עם נקודה שממנה יוצאים שני משיקים חוצה את‬
‫הזווית בין המשיקים‪.‬‬
‫‪ .17‬הזווית הכלואה בין משיק למיתר שווה לזווית ההיקפית הנשענת על המיתר מצדו השני‪.‬‬
‫משפטים העוסקים בשני מעגלים‪:‬‬
‫‪ .18‬קטע המרכזים של שני מעגלים נחתכים חוצה את המיתר המשותף ומאונך לו‪.‬‬
‫‪ .19‬קטע המרכזים (או המשכו) של שני מעגלים משיקים עובר בנקודת ההשקה‪.‬‬
‫משפטים העוסקים במעגל חוסם ומעגל חסום‪:‬‬
‫‪ .20‬מרכז מעגל החוסם משולש הוא מפגש האנכים האמצעיים במשולש‪.‬‬
‫‪ .21‬מרכז מ עגל החסום במשולש הוא מפגש חוצי הזווית במשולש‪.‬‬
‫‪ .22‬במרובע החסום במעגל‪ ,‬סכום כל שתי זוויות נגדיות הוא ‪.180o‬‬
‫‪( .23‬משפט הפוך ל‪ )22-‬אם במרובע סכום זוג זוויות נגדיות הוא ‪ ,180o‬המרובע‬
‫בר חסימה במעגל‪.‬‬
‫‪ .24‬במרובע החוסם מעגל סכום זוג צלעות נגדיות שווה לסכום הזוג השני‪.‬‬
‫‪( .25‬משפט הפוך ל‪ ) 24-‬אם במרובע סכום זוג צלעות נגדיות שווה לסכום הזוג השני‬
‫אז ניתן לחסום בתוכו מעגל‪.‬‬
‫‪ .26‬כל מצולע משוכלל ניתן לחסום במעגל וניתן לחסום בתוכו מעגל‪.‬‬
‫‪82‬‬
83
‫‪ AB ,CD )1‬ו ‪ KL-‬הם מיתרים במעגל שמרכזו ‪ , O‬והם חותכים‬
‫את הקטע ‪ ,MG‬העובר במרכז המעגל‪ ,‬בנקודות ‪E ,F‬‬
‫ו‪ M-‬בהתאמה‪ .‬נתון‪. KL CD , CF  FD :‬‬
‫א‪ .‬הוכח‪. KM  ML :‬‬
‫ב‪ .‬נתון בנוסף כי ‪, AB  MG‬‬
‫הוכח‪. MO  OE :‬‬
‫‪G‬‬
‫‪A‬‬
‫‪K‬‬
‫‪C‬‬
‫‪O‬‬
‫‪E F‬‬
‫‪. ML  EB‬‬
‫‪M‬‬
‫‪D‬‬
‫‪L‬‬
‫‪B‬‬
‫‪550‬‬
‫‪ )2‬חשב את גודל הזוויות ‪ ‬ו‪  -‬במעגל הנתון‪.‬‬
‫‪β‬‬
‫‪500‬‬
‫‪400‬‬
‫‪ AB )3‬ו‪ BC-‬הם מיתרים במעגל שמרכזו ‪. O‬‬
‫נתון‪. BA OC , AGC  60o :‬‬
‫חשב את גודלה של הזווית ‪. AOC‬‬
‫‪ BC ,AD ,AC ,AB )4‬ו‪ CD-‬הם מיתרים במעגל‬
‫שמרכזו ‪( O‬המיתר ‪ AD‬עובר ב‪.)O-‬‬
‫הקטע ‪ BE‬חותך את המיתר ‪ AC‬בנקודה ‪.G‬‬
‫נתון‪. BE CD , BG  GE :‬‬
‫הוכח‪. BC  CD :‬‬
‫‪ )5‬המרובע ‪ ABCD‬הוא מלבן החסום במעגל‪.‬‬
‫מהקדקוד ‪ D‬מעבירים את המיתר ‪ DF‬החותך‬
‫את הצלע ‪ AB‬בנקודה ‪ .E‬ידוע כי‪. AF  CF :‬‬
‫הצלע ‪ AD‬של המלבן תסומן ב‪. a -‬‬
‫א‪ .‬הוכח כי המשולש ‪ DAE‬הוא שווה שוקיים‪.‬‬
‫ב‪ .‬נתון גם כי‪. BC  BF :‬‬
‫‪ .1‬הבע באמצעות ‪ a‬את רדיוס המעגל‪.‬‬
‫‪ .2‬חשב את הזוויות המרכזיות של‬
‫הקשתות‪( AB ; BC :‬אין צורך לסרטט אותן)‪.‬‬
‫‪84‬‬
‫‪α‬‬
‫‪A‬‬
‫‪G‬‬
‫‪C‬‬
‫‪B‬‬
‫‪O‬‬
‫‪A‬‬
‫‪B‬‬
‫‪G‬‬
‫‪C‬‬
‫‪O‬‬
‫‪E‬‬
‫‪D‬‬
‫‪ )6‬מהנקודה ‪ A‬שעל היקף המעגל מעבירים את‬
‫המיתרים ‪ AC , AB‬ו ‪ .AD-‬הקטע ‪ BE‬חותך‬
‫את המיתר ‪ AD‬בנקודה ‪ E‬כך‬
‫שהקטעים ‪ DE‬ו‪ BC-‬שווים‪.‬‬
‫המיתרים ‪ AC‬ו‪ BD-‬שווים זה לזה‪.‬‬
‫א‪ .‬הוכח‪. ABC  BED :‬‬
‫ב‪ .1 .‬הוכח כי המשולש ‪ ABE‬הוא שווה שוקיים‪.‬‬
‫‪ .2‬הוכח כי‪. BAE  CBA  180 :‬‬
‫‪B‬‬
‫‪ )7‬הצלעות ‪ AD ,AB‬ו‪ DC-‬של המקבילית ‪ ABCD‬משיקות‬
‫למעגל בנקודות ‪ L , B‬ו‪ K-‬בהתאמה (ראה שרטוט)‪.‬‬
‫נתון‪. KC  6cm , BC  14cm :‬‬
‫חשב את היקף המקבילית‪.‬‬
‫‪A‬‬
‫‪L‬‬
‫‪C‬‬
‫‪K‬‬
‫‪D‬‬
‫‪A‬‬
‫‪ )8‬הצלעות ‪ AC‬ו‪ BC-‬של המשולש ‪ ABC‬משיקות‬
‫למעגל שמרכזו ‪ , O‬בנקודות ‪ K‬ו ‪ B-‬בהתאמה‪.‬‬
‫הצלע ‪ AB‬עוברת בנקודה ‪.O‬‬
‫נתון‪. AB  15cm , AK  KC :‬‬
‫א‪ .‬חשב את גודלה של זווית ‪. A‬‬
‫ב‪ .‬חשב את אורכו של רדיוס המעגל‪.‬‬
‫‪K‬‬
‫‪O‬‬
‫‪C‬‬
‫‪B‬‬
‫‪H‬‬
‫‪B‬‬
‫‪ )9‬הקדקודים ‪ B‬ו‪ C-‬של המלבן ‪ ABCD‬מונחים על מעגל‪.‬‬
‫הצלע ‪ AD‬משיקה למעגל בנקודה ‪G‬והצלע ‪AB‬‬
‫חותכת את המעגל בנקודה ‪ .H‬הוכח‪. C2  C3 :‬‬
‫(הדרכה‪ :‬סמן ‪.) AGH  ‬‬
‫‪G‬‬
‫‪2 1‬‬
‫‪3‬‬
‫‪C‬‬
‫‪ AB )11‬הוא קוטר במעגל שמרכזו ‪.O‬‬
‫מהנקודה ‪ A‬מעבירים את המיתרים ‪ AC‬ו ‪ AG-‬ואת‬
‫המשיק ‪ AD‬כך שהמשולש‪ ACD‬שווה שוקיים‪.‬‬
‫הישר ‪ CD‬חותך את היקף המעגל בנקודה ‪ ,E‬את‬
‫המיתר ‪ AG‬בנקודה ‪ F‬ועובר דרך מרכז המעגל ‪.O‬‬
‫המיתר ‪ BG‬מקביל לישר החותך ‪.CD‬‬
‫‪85‬‬
‫‪A‬‬
‫‪D‬‬
‫א‪.‬‬
‫ב‪.‬‬
‫ג‪.‬‬
‫חשב את זוויות המשולש ‪.ACD‬‬
‫הוכח כי‪. AF  FG :‬‬
‫רדיוס המעגל יסומן ב‪ . R -‬הוכח כי‪. DC  3R :‬‬
‫‪ )11‬המעגלים שמרכזיהם ‪ M‬ו‪ G-‬משיקים מבחוץ זה לזה‬
‫ומשיקים מבפנים למעגל שמרכזו ‪.O‬‬
‫נתון כי רדיוס המעגל שמרכזו ‪ O‬הוא ‪. 8cm‬‬
‫חשב את היקף המשולש ‪. OMG‬‬
‫‪O‬‬
‫‪M‬‬
‫‪G‬‬
‫‪ AD )12‬הוא התיכון לצלע ‪ BC‬במשולש ‪.ABC‬‬
‫א‪ .‬הוכח‪ :‬אם מרכז המעגל החסום במשולש ‪ABC‬‬
‫נמצא על ‪ AD‬אז המשולש ‪ ABC‬הוא שווה שוקיים‪.‬‬
‫ב‪ .‬בהמשך לסעיף א'‪ ,‬האם מרכז המעגל החוסם את משולש ‪ ABC‬נמצא על ‪?AD‬‬
‫‪ )13‬חשב את גודלה של הזווית ‪ ‬בשרטוט הבא‪:‬‬
‫‪350‬‬
‫‪550‬‬
‫‪500‬‬
‫‪α‬‬
‫‪300‬‬
‫‪ )14‬בטרפז ישר זווית ‪ ABCD‬שבו השוק ‪ AD‬מאונכת‬
‫לבסיסים ‪ AB‬ו‪ DC-‬הנקודות ‪ K‬ו ‪ L-‬נמצאות על‬
‫הצלעות ‪ DC‬ו ‪ AD-‬בהתאמה‪ ,‬כך שהקטעים ‪ BK‬ו‪ CL-‬הם חוצי הזוויות‬
‫ו‪ C -‬בהתאמה‪ .‬חוצי הזוויות נפגשים בנקודה ‪.M‬‬
‫הוכח‪ :‬את המרובע ‪ DKML‬ניתן לחסום במעגל‪.‬‬
‫‪ )15‬המרובע ‪ ABCD‬חסום במעגל‪.‬‬
‫המשכי המיתרים ‪ AB‬ו‪ ED-‬נפגשים בנקודה ‪.F‬‬
‫הקטע ‪ FD‬חותך את היקף המעגל בנקודה ‪ E‬כך‬
‫שמתקיים‪. AB  AE :‬‬
‫נתון כי הזווית ‪ BCD‬היא ישרה‪.‬‬
‫א‪ .‬הוכח כי הקטע ‪ DF‬שווה לקוטר המעגל‪.‬‬
‫נתון כי‪ DF  BF :‬וכי רדיוס המעגל הוא ‪ 12‬ס"מ‪.‬‬
‫ב‪ .‬הוכח כי המרובע ‪ AEDB‬הוא טרפז‪.‬‬
‫ג‪ .‬חשב את היקף הטרפז ‪.AEDB‬‬
‫‪ )16‬חשב את גודלו של ‪ x‬בשרטוט הבא‪:‬‬
‫‪86‬‬
‫‪B‬‬
87
‫‪. AOC  40 )3   35 ,   95 )2‬‬
‫‪2‬‬
‫‪ )5‬ב‪ 1.3a .1 .‬‬
‫‪2‬‬
‫‪ )8‬א‪A  30 .‬‬
‫‪  70 )13‬‬
‫‪AB  135 .2 R  a 1 ‬‬
‫; ‪BC  45‬‬
‫ב‪ 5 .‬ס"מ‪ )11 .‬א‪30 , 30 , 120  .‬‬
‫‪ 48 )7‬ס"מ = ‪. P‬‬
‫‪ 16 )11‬ס"מ = ‪. P‬‬
‫‪ )15‬ג‪ 60 .‬ס"מ‪. x  2 )16 .‬‬
‫פרופורציה דמיון‪:‬‬
‫פרופורציה‪:‬‬
‫משפט תאלס‪:‬‬
‫‪ .1‬שני ישרים מקבילים החותכים שוקי זווית מקצים עליהן קטעים‬
‫פרופורציוניים‪.‬‬
‫‪ .2‬משפט הפוך‪ :‬אם שני ישרים החותכים שוקי זווית מקצים עליהן קטעים‬
‫פרופורציוניים הישרים מקבילים‪.‬‬
‫‪AD AE‬‬
‫‪‬‬
‫‪ .3‬משפט תאלס ‪ +‬ההפוך‪:‬‬
‫‪DB EC‬‬
‫‪E‬‬
‫‪. DE BC ‬‬
‫‪AD AE DE‬‬
‫‪‬‬
‫‪‬‬
‫‪ .4‬משפט תאלס המורחב ‪ +‬ההפוך‪:‬‬
‫‪AB AC BC‬‬
‫‪A‬‬
‫‪D‬‬
‫‪C‬‬
‫‪. DE BC ‬‬
‫‪BE AE AB‬‬
‫‪‬‬
‫‪‬‬
‫‪ .5‬משפט תאלס "שעון חול" ‪ +‬ההפוך‪:‬‬
‫‪ED EC DC‬‬
‫‪B‬‬
‫‪A‬‬
‫‪B‬‬
‫‪. AB DC ‬‬
‫‪E‬‬
‫‪D‬‬
‫‪C‬‬
‫משפט חוצה הזווית‪:‬‬
‫‪ .6‬חוצה זווית במשולש מחלק את הצלע שמול הזווית ביחס‬
‫הזהה ליחס בין הצלעות שביניהן הוא כלוא ולהפך‪.‬‬
‫אם‪A1  A2 :‬‬
‫‪AB AC‬‬
‫‪‬‬
‫אז‪:‬‬
‫‪BD DC‬‬
‫ולהיפך‪.‬‬
‫‪88‬‬
‫‪A‬‬
‫‪2 1‬‬
‫‪C‬‬
‫‪D‬‬
‫‪B‬‬
89
‫דמיון משולשים‪:‬‬
‫משולשים דומים הם משולשים ששווים זה לזה בכל זוויותיהם ושצלעותיהם‬
‫שומרות בהתאמה על אותו יחס‪.‬‬
‫‪DEF‬‬
‫‪F‬‬
‫‪E, C‬‬
‫‪A‬‬
‫‪ABC‬‬
‫‪D, B‬‬
‫‪AB AC BC‬‬
‫‪‬‬
‫‪‬‬
‫‪DE DF EF‬‬
‫‪D‬‬
‫‪A‬‬
‫‪F‬‬
‫‪E‬‬
‫‪C‬‬
‫‪B‬‬
‫משפטי הדמיון‪:‬‬
‫‪ .1‬משפט דמיון זווית‪ -‬זווית (ז‪.‬ז)‪ :‬אם בין שני משולשים שוות שתי זוויות אז‬
‫המשולשים דומים‪.‬‬
‫‪ .2‬משפט דמיון צלע ‪-‬זווית‪ -‬צלע (צ‪.‬ז‪.‬צ)‪ :‬אם בין שני משולשים שתי צלעות שומרות‬
‫על אותו יחס והזוויות שבניהן שווה אז המשולשים דומים‪.‬‬
‫‪ .3‬משפט דמיון צלע ‪-‬צלע ‪-‬צלע (צ‪.‬צ‪.‬צ)‪ :‬אם בין שני משולשים שלוש הצלעות‬
‫שומרות על אותו יחס אז המשולשים דומים‪.‬‬
‫‪ .4‬משפט דמיון צלע ‪-‬צלע ‪-‬והזווית הגד ולה (צ‪.‬צ‪.‬ז)‪ :‬אם בין שני משולשים שתי‬
‫לצעות שומרות על אותו יחס והזווית שמול הצלע הגדולה מביניהם שווה אז‬
‫המשולשים דומים‪.‬‬
‫יחס בין גדלים במשולשים דומים‪:‬‬
‫‪ .1‬בין שני משולשים דומים היחס בין הגבהים‪ ,‬התיכונים‪ ,‬חוצי הזווית‪ ,‬ההיקפים‪,‬‬
‫רדיוס המעגל החוסם ורדיוס המעגל החסום הוא כיחס הדמיון‪.‬‬
‫‪ .2‬היחס בין שטחי משולשים דומים הוא ריבוע יחס הדמיון‪.‬‬
‫‪90‬‬
‫פרופורציות במשולש ישר זווית‪:‬‬
‫‪ .1‬במשולש ישר זווית‪ ,‬הגובה ליתר בריבוע שווה למכפלת היטלי הניצבים על היתר‪.‬‬
‫‪ .2‬במשולש ישר זווית‪ ,‬ניצב בריבוע שווה למכפלת היתר והיטל הניצב על היתר‪.‬‬
‫‪( .3‬משפט הפוך ל‪ ) 1-‬אם במשולש גובה לצלע אחת בריבוע שווה למכפלת היטלי‬
‫הצלעות האחרות על צלע זאת‪ ,‬המשולש ישר זווית‪.‬‬
‫פרופורציות במעגל‪:‬‬
‫‪ .1‬אם שני מיתרים מחתכים במעגל‪ ,‬אז מכפלת קטעי המיתר האחד שווה‬
‫למכפלת קטעי המיתר השני‪.‬‬
‫‪ .2‬אם מנקודה שמחוץ למעגל יוצאים שני חותכים למעגל‪ ,‬אז מכפלת חותך אחד‬
‫בחלקו החיצוני שווה למכפלת החותך השני בחלקו החיצוני‪.‬‬
‫‪ .3‬אם מנקודה שמחוץ למעגל יוצאים חותך ומשיק למעגל‪ ,‬אז מכפלת החותך‬
‫בחלקו החיצוני שווה לריבוע המשיק‪.‬‬
‫‪ )1‬מצא את ערכו של ‪ x‬בשרטוטים הבאים‪:‬‬
‫‪ )2‬בטרפז ‪ ABCD‬האלכסונים נפגשים בנקודה ‪.Q‬‬
‫בנקודה ‪ Q‬העבירו קטע המקביל לבסיסי הטרפז וחותך‬
‫את שוקי הטרפז בנקודות ‪ M‬ו‪ N-‬כמתואר בשרטוט‪.‬‬
‫נתון‪. QB  3cm , DQ  9cm , DC  18cm :‬‬
‫‪C‬‬
‫חשב את גודל הקטע ‪. MQ‬‬
‫‪91‬‬
‫‪A‬‬
‫‪B‬‬
‫‪N‬‬
‫‪Q‬‬
‫‪M‬‬
‫‪D‬‬
92
‫‪AK MC AL‬‬
‫‪‬‬
‫‪‬‬
‫‪ )3‬בשרטוט נתון‪:‬‬
‫‪KC BM LB‬‬
‫‪A‬‬
‫‪.‬‬
‫א‪ .‬הוכח‪ :‬המרובע ‪ KLMC‬הוא מקבילית‪.‬‬
‫ב‪ .‬נתון‪. BC  10cm , AL  1.5BL :‬‬
‫‪K‬‬
‫‪L‬‬
‫חשב את אורך הקטע ‪.LK‬‬
‫‪C‬‬
‫‪B‬‬
‫‪M‬‬
‫‪H‬‬
‫‪ )4‬הטרפז ‪ ABCD‬הוא שווה שוקיים‪.‬‬
‫חוסמים מעגל בתוך הטרפז אשר משיק לו‬
‫בנקודות ‪ F ,E‬ו‪ G-‬כמתואר באיור‪.‬‬
‫הקטעים ‪ DF‬ו‪ CE-‬חוצים את זוויות הטרפז‬
‫ונחתכים בנקודה ‪.M‬‬
‫א‪ .‬הוכח כי הנקודה ‪ M‬היא מרכז‬
‫המעגל החסום‪.‬‬
‫ב‪ .‬חשב את זוויות הטרפז‪.‬‬
‫ג‪ .‬ממשיכים את ‪ GF‬ואת ‪ AD‬כך‬
‫שהם נפגשים בנקודה ‪.H‬‬
‫‪EM‬‬
‫חשב את היחס‬
‫‪FH‬‬
‫‪G‬‬
‫‪B‬‬
‫‪A‬‬
‫‪E‬‬
‫‪F‬‬
‫‪M‬‬
‫‪C‬‬
‫‪D‬‬
‫‪.‬‬
‫‪ )5‬במשולש ‪ ABC‬מעבירים את התיכונים ‪ BD‬ו‪CE-‬‬
‫אשר נפגשים בנקודה ‪ .M‬במשולש ‪ BDC‬מעבירים את‬
‫התיכונים ‪ CL‬ו‪ BK-‬הנפגשים בנקודה ‪.O‬‬
‫א‪ .‬הוכח כי‪. 3LM  BL :‬‬
‫ב‪ .‬הוכח כי‪. AC MO :‬‬
‫ג‪ .‬נתון‪ . SBLC  27 :‬חשב את שטח המשולש ‪.MOL‬‬
‫‪A‬‬
‫‪ )6‬הנקודות ‪ C ,B ,A‬ו‪ D-‬מונחות על היקפו של מעגל שמרכזו ‪.O‬‬
‫הרדיוס ‪ DO‬חוצה את הזווית ‪. BOC‬‬
‫נתון‪. BC  10cm , AC  12cm , AB  8cm :‬‬
‫חשב את אורכו של הקטע ‪.MN‬‬
‫‪O‬‬
‫‪C‬‬
‫‪M‬‬
‫‪D‬‬
‫‪93‬‬
‫‪N‬‬
‫‪B‬‬
‫‪ )7‬במעגל שרדיוסו הוא ‪ 10‬ס"מ המיתרים ‪ AB‬ו‪ BC-‬מאונכים זה לזה‪.‬‬
‫הנקודה ‪ D‬היא אמצע הקשת ‪. BC‬‬
‫הקטע ‪ AD‬חותך את המיתר ‪ BC‬בנקודה ‪.E‬‬
‫אורך המיתר ‪ AB‬הוא ‪ 12‬ס"מ‪.‬‬
‫א‪ .‬חשב את אורך הקטע ‪.BE‬‬
‫מהנקודה ‪ D‬מעבירים מיתר החותך את המיתר ‪BC‬‬
‫בנקודה ‪ F‬ומקביל למיתר ‪.AB‬‬
‫ב‪ .‬הוכח כי מיתר זה עובר דרך מרכז המעגל‪.‬‬
‫ג‪ .‬חשב את אורך הקטע ‪.FE‬‬
‫‪ )8‬נתון משולש ‪ .ABC‬הקטע ‪ AE‬חוצה את זווית ‪ A‬של המשולש‪.‬‬
‫ממשיכים את ‪ AE‬עד לנקודה ‪ D‬כך שנוצר המשולש ‪.BDC‬‬
‫‪ F‬היא נקודה על הצלע ‪ BC‬המקיימת‪. DF  FE  DC :‬‬
‫הצלע ‪ AB‬מקבילה לצלע ‪.DC‬‬
‫א‪ .‬הוכח כי‪. AC  EF :‬‬
‫ב‪.‬‬
‫‪AB FE‬‬
‫‪‬‬
‫‪BE CE‬‬
‫ג‪.‬‬
‫הָ ְמשך את הקטע ‪ DF‬עד לנקודה ‪ H‬שעל הצלע ‪.AB‬‬
‫ידוע כי המרובע ‪ ACDH‬הוא בר חסימה‪.‬‬
‫חשב את זוויות המשולש ‪.DEF‬‬
‫‪.‬‬
‫‪ )9‬במשולש ‪ ABC‬העבירו את הקטע‬
‫הוכח‪. AKB ABC :‬‬
‫‪BK‬‬
‫כך ש‪. AKB  ABC -‬‬
‫‪A‬‬
‫‪K‬‬
‫‪B‬‬
‫‪C‬‬
‫‪A‬‬
‫‪ . BKMC‬המשיכו את הצלע ‪BK‬‬
‫‪ )11‬נתונה מקבילית‬
‫הקטע ‪ AC‬חותך את הצלע‬
‫הוכח‪. LC  BC  LM  AC :‬‬
‫‪KM‬‬
‫עד לנקודה ‪. A‬‬
‫בנקודה ‪. L‬‬
‫‪L‬‬
‫‪M‬‬
‫‪C‬‬
‫‪94‬‬
‫‪K‬‬
‫‪B‬‬
‫‪ )11‬מעבירים משיק ‪ AE‬למעגל הנתון באיור‪.‬‬
‫מנקודת ההשקה מעבירים את המיתרים ‪ AB‬ו‪AC-‬‬
‫כך שנוצר המשולש ‪ .ABC‬ידוע כי‪. AC  BC :‬‬
‫המשך המיתר ‪ BC‬נפגש עם המשיק בנקודה ‪.E‬‬
‫המיתר ‪ AB‬חוצה את זווית ‪. CBD‬‬
‫א‪ .‬הוכח כי הקטע ‪ BD‬מקביל למיתר ‪.AC‬‬
‫ב‪ .‬הוכח‪ ABD CBA :‬וכתוב את יחס הדמיון‪.‬‬
‫ג‪.‬‬
‫‪DE BD‬‬
‫‪‬‬
‫‪BE AB‬‬
‫‪.‬‬
‫‪ )12‬נתון משולש ‪ .ABC‬על הצלע ‪ AB‬של המשולש ‪ ABC‬בונים משולש שווה צלעות ‪.ABD‬‬
‫הצלע ‪ AC‬חותכת את הצלע ‪ BD‬בנקודה ‪ E‬אשר ממנה מעבירים ישר ‪ EF‬המקביל‬
‫לצלע ‪ .BC‬נתון כי‪. DCB  40 , DBC  80 :‬‬
‫א‪ .‬הוכח כי המשולשים ‪ ABE‬ו‪ CDE-‬דומים‪.‬‬
‫ב‪ .‬הוכח‪. FC  CE  AE  DF :‬‬
‫ג‪ .‬נתון כי‪. BC  1.5  EF :‬‬
‫‪AE 1‬‬
‫‪ .1‬הוכח‪ :‬‬
‫‪CE 2‬‬
‫‪.‬‬
‫‪S ABE‬‬
‫‪ .2‬חשב את יחס השטחים‪:‬‬
‫‪SCDE‬‬
‫‪.‬‬
‫‪ )13‬מהקדקוד ‪ C‬של המשולש ‪ BCD‬מעבירים את הקטע ‪AC‬‬
‫כך שהמשולש ‪ ACD‬הוא שווה שוקיים ‪.  AC  AD ‬‬
‫הנקודה ‪ F‬נמצאת על הצלע ‪ CD‬כך שמתקיים‪:‬‬
‫‪. D  CBF , 3  ACD  BEC‬‬
‫א‪ .‬הוכח כי הקטע ‪ BF‬חוצה את זווית ‪. B‬‬
‫ב‪ .‬הוכח כי‪.AEB FEC :‬‬
‫‪BE AE‬‬
‫‪‬‬
‫ג‪ .‬הוכח כי‪:‬‬
‫‪BC FC‬‬
‫‪.‬‬
‫‪ )14‬המעגלים שמרכזם בנקודות ‪ M‬ו‪ N-‬משיקים זה‬
‫לזה מבפנים בנקודה ‪ A‬כך שהיקף‬
‫המעגל הפנימי עובר בנקודה ‪.M‬‬
‫דרך הנקודה ‪ A‬מעבירים משיק‪.‬‬
‫‪ AB‬הוא קוטר במעגלים ו‪ C-‬היא נקודה‬
‫הנמצאת על היקף המעגל הפנימי כך‬
‫שהמיתר ‪ BD‬משיק למעגל הפנימי בנקודה זו‪.‬‬
‫‪95‬‬
‫א‪ .‬הוכח‪ ABD CBN :‬וחשב את יחס הדמיון‪.‬‬
‫ב‪ .‬נתון כי‪ . AD  8 :‬חשב את רדיוס המעגל הגדול‪.‬‬
‫ג‪ .‬הוכח‪. 2CD  BC :‬‬
‫‪ )15‬נתונים שני מעגלים בעלי רדיוס זהה ‪ M‬ו‪.N-‬‬
‫מעבירים שני משיקים למעגלים ‪ AB‬ו‪ CD-‬הנחתכים בנקודה ‪.K‬‬
‫מעבירים את הרדיוסים ‪ AN‬ו‪ DN-‬במעגל השמאלי ו‪ BM-‬ו‪ CM-‬במעגל הימני‪.‬‬
‫א‪ .‬הוכח‪. KN  KM :‬‬
‫ב‪ .‬הוכח כי המרובע ‪ ACMN‬הוא‬
‫טרפז שווה שוקיים‪.‬‬
‫ג‪ .‬רדיוס המעגלים הוא ‪ R‬וידוע כי‬
‫המשולש ‪ BKC‬הוא שווה צלעות‪.‬‬
‫הבע באמצעות ‪ R‬את היקף הטרפז ‪.ACMN‬‬
‫‪ )16‬על הצלעות של המשולש ‪ ABC‬הקצו את הנקודות ‪ D‬ו‪ E-‬כך שהמרובע ‪AEDB‬‬
‫הוא בר חסימה‪ .‬הנקודה ‪ D‬מחלקת את הצלע ‪ BC‬כך‬
‫שהקטע ‪ BD‬גדול פי ‪ 3‬מהקטע ‪.DC‬‬
‫א‪ .‬הוכח‪. ABC DEC :‬‬
‫ב‪ .‬נתון גם כי‪. AC  CE  36 :‬‬
‫חשב את אורך הקטע ‪.DC‬‬
‫ג‪ .‬מעבירים מהקודקוד ‪ A‬את הקטע ‪ AF‬המקביל‬
‫לקטע ‪ .DE‬נתון כי‪. AC  9 :‬‬
‫‪DF‬‬
‫חשב את היחס‪:‬‬
‫‪BC‬‬
‫‪.‬‬
‫‪ )17‬הישרים ‪ AB‬ו‪ AC-‬חותכים את המעגל בנקודות ‪ D‬ו‪ E-‬בהתאמה כך שהמיתרים‬
‫‪ BD‬ו‪ BC-‬מאונכים זה לזה‪ .‬הקטע ‪ CG‬חוצה את הקשת הקטנה ‪ BGD‬וחותך‬
‫את המיתר ‪ BD‬בנקודה ‪.F‬‬
‫‪AC 13‬‬
‫נתון‪:‬‬
‫‪‬‬
‫‪AB 12‬‬
‫‪ .‬נסמן‪. AB  t :‬‬
‫א‪ .‬הבע באמצעות ‪ t‬את אורך המיתר ‪.BC‬‬
‫‪BF 3‬‬
‫‪‬‬
‫ב‪ .‬נתון כי רדיוס המעגל הוא ‪ 5‬ס"מ וכי‪:‬‬
‫‪DF 5‬‬
‫חשב את אורך הקטע ‪.AB‬‬
‫ג‪ .‬חשב את‪. A :‬‬
‫‪ )18‬המשולש ‪ ABC‬חסום במעגל‪.‬‬
‫‪ A‬גובה לצלע ‪ BC‬ו‪ AE-‬קוטר במעגל‪.‬‬
‫א‪ .‬הוכח‪. BAD  EAC :‬‬
‫‪96‬‬
‫‪.‬‬
‫נתון גם כי‪. CE  21 , AD  6 , CD  8 :‬‬
‫ב‪ .‬חשב את רדיוס המעגל‪.‬‬
‫‪ )19‬הקטע ‪ AB‬משיק למעגל בנקודה ‪ .A‬מהנקודה ‪ B‬מעבירים ישר חותך למעגל‬
‫החותך אותו בנקודות ‪ C‬ו‪.D-‬‬
‫‪ E‬היא נקודה על המעגל כך ש ‪. AEC  90 -‬‬
‫נתון כי המיתר ‪ AC‬חוצה את זווית ‪.BCE‬‬
‫א‪ .‬הוכח‪. ABC EAC :‬‬
‫ב‪.‬‬
‫ג‪.‬‬
‫‪BC  CE‬‬
‫נסמן ב‪ R -‬את רדיוס המעגל‪ .‬הוכח‪:‬‬
‫‪2‬‬
‫‪.R‬‬
‫איזה מרובע יהיה המרובע ‪ADCE‬‬
‫אם יתקיים‪ . 2CE  BC :‬נמק‪.‬‬
‫‪ )21‬במשולש ‪ ABC‬הנקודות ‪ D‬ו‪ E-‬נמצאות על הצלעות ‪ BC‬ו‪ AB-‬בהתאמה‪.‬‬
‫נתון כי‪. ADC  BED , DE AC :‬‬
‫א‪ .‬הוכח כי המשולשים ‪ ADC‬ו ‪ BED-‬דומים‪.‬‬
‫ב‪ .‬הוכח‪. AD  BD  AB  DE :‬‬
‫ג‪ .‬ידוע כי הנקודה ‪ D‬מחלקת את‬
‫‪BD 4‬‬
‫הצלע ‪ BC‬באופן הבא‪ :‬‬
‫‪DC 5‬‬
‫וכי‪. AD  BD  16 :‬‬
‫חשב את המכפלה‪. AB  AC :‬‬
‫‪.‬‬
‫‪A‬‬
‫‪ )21‬המשולש ‪ ABC‬חסום במעגל שמרכזו ‪ . O‬הצלע ‪BC‬‬
‫היא קוטר המעגל‪ .‬הקטע ‪ BM‬מאונך לרדיוס ‪. OD‬‬
‫נתון‪. AC  2OM :‬‬
‫‪C‬‬
‫‪O‬‬
‫א‪ .‬הוכח‪. AB  2BD :‬‬
‫ב‪.‬‬
‫‪S BOM‬‬
‫‪S BAC‬‬
‫‪M‬‬
‫‪B‬‬
‫‪.‬‬
‫‪D‬‬
‫‪ ABC )22‬הוא משולש שווה שוקיים ( ‪ ) AB  AC‬שבו השוק גדולה‬
‫פי ‪ 2‬מהבסיס‪ .‬המשיכו את הבסיס משני צדדיו עד לנקודות ‪D‬‬
‫ו‪ E-‬כך שמתקיים ‪ BC  CE‬ו‪. D  CAE -‬‬
‫נתון‪. SABC  m :‬‬
‫בטא באמצעות ‪ m‬את שטח המשולש ‪.ADE‬‬
‫‪97‬‬
‫‪E‬‬
‫‪C‬‬
‫‪A‬‬
‫‪B‬‬
‫‪D‬‬
‫‪ )23‬המרובע ‪ ABCD‬הוא טרפז‪.  AB CD  ,‬‬
‫מעבירים את קטע האמצעים ‪ EF‬החותך את אלכסון‬
‫הטרפז ‪ BD‬בנקודה ‪.K‬‬
‫ידוע כי הקטע ‪ AK‬מקביל לשוק ‪ BC‬של הטרפז‪.‬‬
‫‪98‬‬
‫א‪ .‬הוכח כי המרובע ‪ ABFK‬הוא מקבילית‪.‬‬
‫ב‪ .‬נסמן‪ . SBKF  S :‬הבע באמצעות ‪ S‬את שטח הטרפז ‪.ABCD‬‬
‫‪ )24‬בין המשיקים המקבילים ‪ m‬ו‪ n -‬מעבירים‬
‫מעגל כך ש ‪ AB-‬הוא הקוטר היוצא משתי נקודות‬
‫ההשקה שלהם‪ .‬הנקודות ‪ D‬ו‪ C-‬נמצאות על‬
‫המשכי המשיקים כך שהמרובע ‪ ABCD‬הוא טרפז‪.‬‬
‫אלכסוני הטרפז נפגשים בנקודה ‪ E‬שנמצאת‬
‫על היקף המעגל‪ .‬ידוע כי‪. SABC  3  SDAB :‬‬
‫שטח המשולש ‪ ADE‬יסומן ב ‪. S -‬‬
‫בטא באמצעות ‪ S‬את שטח הטרפז ‪.ABCD‬‬
‫‪ )25‬נתון משולש ‪ .ABC‬על הצלע ‪ BC‬של המשולש ‪ABC‬‬
‫בונים משולש נוסף ‪ .BDC‬הצלעות ‪ DC‬ו‪ AB-‬נחתכות‬
‫בנקודה ‪ .M‬הצלע ‪ AB‬חוצה את זווית ‪B‬‬
‫וידוע כי‪. 2 ACD  B :‬‬
‫א‪ .‬הוכח‪. ACM DBM :‬‬
‫‪AC AM‬‬
‫ב‪ .‬הוכח‪:‬‬
‫‪‬‬
‫‪BC CM‬‬
‫‪AM 8‬‬
‫וכי אורך הצלע ‪ BD‬הוא ‪ 6‬ס"מ‪.‬‬
‫ג‪ .‬נתון כי‪ :‬‬
‫‪CM 5‬‬
‫‪.‬‬
‫‪S BDM‬‬
‫סכום הצלעות ‪ AC‬ו‪ BC-‬הוא ‪ 19.5‬ס"מ‪ .‬חשב את היחס‪:‬‬
‫‪S BMC‬‬
‫‪.‬‬
‫‪ AB )26‬הוא קוטר במעגל שמרכזו ‪ .O‬מהנקודה ‪ C‬שעל היקף המעגל מעבירים את‬
‫הרדיוס ‪ CO‬ואת המיתר ‪ CD‬החותך את הקוטר בנקודה ‪. E‬‬
‫מהנקודה ‪ D‬מעבירים את המיתרים ‪ BD‬ו ‪.AD-‬‬
‫‪AD AE‬‬
‫‪‬‬
‫ידוע כי המיתר ‪ CD‬מקיים‪:‬‬
‫‪BD BE‬‬
‫א‪.‬‬
‫ב‪.‬‬
‫ג‪.‬‬
‫‪ .‬נתון‪. AD  DE :‬‬
‫הוכח כי הרדיוס ‪ CO‬מאונך לקוטר ‪.AB‬‬
‫הוכח‪. COE BDA :‬‬
‫נתון כי אורך המיתר ‪ BD‬הוא ‪ 16.2‬ס"מ‬
‫ואורך הקטע ‪ CE‬הוא ‪ 10‬ס"מ‪.‬‬
‫‪ .1‬חשב את רדיוס המעגל‪.‬‬
‫‪SCOE‬‬
‫‪ .2‬חשב את היחס‪:‬‬
‫‪S BDA‬‬
‫‪.‬‬
‫‪99‬‬
100
‫‪ AB )27‬הוא קוטר במעגל‪ .‬מהנקודה ‪ A‬מעבירים מיתר ‪.AC‬‬
‫הנקודה ‪ D‬נמצאת מחוץ למעגל וממנה מעבירים‬
‫משיק ‪ CD‬וישר חותך ‪ .DE‬ידוע כי הישר ‪ DE‬חותך את‬
‫הקוטר ‪ AB‬בנקודה ‪ G‬ומאונך למיתר ‪ AC‬בנקודה ‪.H‬‬
‫א‪ .‬הוכח‪. ACD  BGE :‬‬
‫ב‪.‬‬
‫‪S‬‬
‫‪AH‬‬
‫‪4‬‬
‫נתון כי‪ AHG  :‬חשב את היחס‪:‬‬
‫‪AC‬‬
‫‪SGHCB 5‬‬
‫‪.‬‬
‫‪ AB )28‬ו‪ CD-‬הם קטרים במעגל שמרכזו ‪.O‬‬
‫מעבירים מיתר החותך את ‪ AB‬בנקודה ‪ M‬כך שמתקיים‪2AM  BM :‬‬
‫ואת ‪ CD‬בנקודה ‪ F‬כך שמתקיים‪ . FM  CD :‬ידוע כי זווית ‪ BMF‬היא ‪. 30‬‬
‫מעבירים את המיתרים ‪ AC‬ו ‪ AD-‬כך שנוצר המשולש ‪.ACD‬‬
‫א‪ .‬הוכח‪. CAB  BMF :‬‬
‫ב‪ .1 .‬הוכח כי המשולשים ‪ ADC‬ו‪ FOM-‬דומים‪.‬‬
‫‪ .2‬פי כמה קטן הקטע ‪ FO‬מרדיוס המעגל?‬
‫ג‪ .‬מעבירים מהקדקוד ‪ D‬של המשולש ‪ ACD‬קטע‬
‫העובר דרך הנקודה ‪ M‬וחותך את המיתר ‪AC‬‬
‫בנקודה ‪ .G‬חשב פי כמה גדול שטח‬
‫המשולש ‪ DGC‬משטח המשולש ‪.MOF‬‬
‫‪ )29‬מצא את ערכם של ‪ x‬ו ‪ y -‬בשרטוט הבא‪:‬‬
‫‪ )31‬במשולש ישר זווית שאורכי ניצביו ‪ m‬ו‪ n -‬נתון כי אורך הגובה ליתר הוא ‪. h‬‬
‫‪1‬‬
‫‪1‬‬
‫‪1‬‬
‫הראה שמתקיים‪ 2  2 :‬‬
‫‪2‬‬
‫‪h‬‬
‫‪m n‬‬
‫(אין צורך ברישום מסודר של הוכחה)‪.‬‬
‫‪ )31‬הוכח את המשפט‪ :‬אם במשולש גובה לצלע אחת בריבוע שווה למכפלת היטלי‬
‫הצלעות האחרות על צלע זאת‪ ,‬המשולש ישר זווית‪.‬‬
‫‪101‬‬
102
‫‪ )32‬חשב את גודלם של ‪ x‬ו ‪ y -‬בשרטוטים הבאים‪:‬‬
‫ב‪.‬‬
‫א‪.‬‬
‫‪2‬‬
‫‪4‬‬
‫‪2‬‬
‫‪3‬‬
‫‪4‬‬
‫‪8‬‬
‫‪5‬‬
‫‪ )33‬הוכח את המשפט‪ :‬אם מנקודה שמחוץ למעגל יוצאים חותך ומשיק למעגל‪,‬‬
‫מכפלת החותך בחלקו החיצוני שווה לריבוע המשיק‪.‬‬
‫‪ )34‬הוכח את המשפט‪ :‬אם מנקודה שמחוץ למעגל יוצאים שני חותכים למעגל‪,‬‬
‫מכפלת חותך אחד בחלקו החיצוני שווה למכפלת החותך השני בחלקו החיצוני‪.‬‬
‫‪2‬‬
‫‪3‬‬
‫‪ )1‬א‪ x  1 .‬ב‪ )3 MQ  4.5cm )2 x  2 .‬ב‪ )4 LK  6cm .‬ב‪ 60 ,120 .‬ג‪. .‬‬
‫‪ )5‬ג‪ )7 MN  1cm )6 3 .‬א‪ BE  6 .‬ג‪ )8 EF  2 .‬ג‪72 , 72 , 36 .‬‬
‫‪SABE 1‬‬
‫‪ )12‬ג‪ .2 .‬‬
‫‪SCDE 4‬‬
‫‪5‬‬
‫‪ )17‬א‪ BC  t .‬ב‪ AB  14.4 .‬ג‪ )18 A  22.61 .‬ב‪ 5.5 .‬ס"מ ‪ )19‬ג‪ .‬ריבוע‪.‬‬
‫‪12‬‬
‫‪SBOM 1‬‬
‫‪ )23 SADE  6m )22‬ב‪. 16S )24 6S .‬‬
‫‪ )21‬ג‪ )21 AB  AC  36 .‬‬
‫‪SBAC 4‬‬
‫‪SCOE 25‬‬
‫‪AH 2‬‬
‫‪S‬‬
‫‪ )27‬ב‪ .‬‬
‫‪.‬‬
‫‪ )25‬ג‪ )26 BDM  0.8 .‬ג‪.2 R  9 .1 .‬‬
‫‪‬‬
‫‪SBDA 81‬‬
‫‪AC 3‬‬
‫‪SBMC‬‬
‫‪BF 7‬‬
‫‪ )14‬ב‪ 4 .‬ס"מ‪ )15 .‬ג‪ )16 9R .‬ב‪ 3 .‬ס"מ ג‪.‬‬
‫‪‬‬
‫‪BC 16‬‬
‫‪ )28‬ב‪ .2 .‬קטן פי ‪ 6‬ג‪ .‬שטח המשולש ‪ DGC‬גדול פי ‪ 18‬משטח המשולש ‪.MOF‬‬
‫‪ )32 y  6 , x  52 )29‬א‪ y  2 , x  3 .‬ב‪. x  5 , y  3 .‬‬
‫‪103‬‬
‫שאלות שונות‪:‬‬
‫שאלות ללא פרופורציה‪:‬‬
‫‪ )1‬במשולש ‪ ABC‬מעבירים את שלושת הגבהים‪. AD , BE , CF :‬‬
‫הגבהים נפגשים בנקודה ‪. Q‬‬
‫א‪ .‬הוכח‪. ACF  ABE :‬‬
‫ב‪ .‬הוכח כי מרובע ‪ QDCE‬הוא‬
‫מרובע בר‪-‬חסימה‪.‬‬
‫ג‪.‬‬
‫הוכח‪. ADF  ADE :‬‬
‫‪ )2‬במשולש ‪ E , ABC‬אמצע ‪ F , AB‬על ‪ BC‬ו ‪ EF‬מקביל ל‪. AC -‬‬
‫‪ G‬על ‪ AC‬ו‪ EG -‬מקביל ל‪. BC -‬‬
‫בלי להשתמש במשפטים על קו אמצעים במשולש הוכח‪:‬‬
‫א‪ .‬המשולש ‪ AEG‬והמשולש ‪ EBF‬חופפים‪.‬‬
‫ב‪ .‬על פי הסעיף הקודם‪ ,‬הוכח כי קטע במשולש החוצה צלע של המשולש‬
‫ומקביל לצלע השלישית במשולש הוא קטע אמצעים‪.‬‬
‫‪ )3‬במשולש שווה שוקיים ‪, ( AB  AC ) ABC‬‬
‫‪ BD‬הוא תיכון לשוק ‪. CBD  30 , AC‬‬
‫א‪ .‬הוכח כי משולש ‪ ABC‬הוא משולש שווה צלעות‪.‬‬
‫(הדרכה‪ :‬הורד אנכים ‪ AF‬ו ‪ DE -‬לבסיס ‪BC‬‬
‫‪1‬‬
‫‪1‬‬
‫‪2‬‬
‫‪2‬‬
‫‪A‬‬
‫‪D‬‬
‫והוכח כי‪) DE   AF   BD :‬‬
‫ב‪ .‬אם נתון כי אורך התיכון ‪ BD‬הוא ‪ a‬ס"מ‪,‬‬
‫חשב אם אורך צלע המשולש ואת שטחו‪.‬‬
‫‪B‬‬
‫‪C‬‬
‫‪A‬‬
‫‪ )4‬במשולש ‪ ) C  90 ( ABC‬הנקודה ‪ E‬מונחת‬
‫על היתר ‪ . AB‬מהנקודה ‪ E‬מעבירים אנך ליתר‪,‬‬
‫החותך את המשך הניצב ‪ BC‬בנקודה ‪ F‬ואת הניצב ‪AC‬‬
‫בנקודה ‪. D‬‬
‫‪E‬‬
‫‪D‬‬
‫נתון כי‪ 10 :‬ס"מ ‪ 12 , AD ‬ס"מ ‪ 8 , EB ‬ס"מ ‪. AE ‬‬
‫הוכח כי‪. ADE  DFC :‬‬
‫‪B‬‬
‫‪104‬‬
‫‪C‬‬
‫‪DF‬‬
‫‪ )5‬מנקודה ‪ M‬הנמצאת מחוץ למעגל מעבירים חותך ‪MPQ‬‬
‫‪M‬‬
‫ומשיק ‪ . MN‬מנקודה ‪ K‬הנמצאת בהמשך ‪ MPQ‬מעבירים‬
‫ישר מקביל למיתר ‪, QN‬החותך את המשך המשיק ‪MN‬‬
‫בנקודה ‪. L‬‬
‫א‪ .‬הוכח כי‪. QNL  NPQ :‬‬
‫ב‪ .‬הוכח כי המרובע ‪ KPNL‬הוא בר‪-‬חסימה‪.‬‬
‫‪P‬‬
‫‪Q‬‬
‫‪N‬‬
‫‪K‬‬
‫‪L‬‬
‫‪ )6‬נתונה מקבילית ‪. ABCD‬‬
‫על הצלע ‪ AB‬בונים ריבוע ‪ ABEF‬ועל‬
‫‪F‬‬
‫‪E‬‬
‫הצלע ‪ AD‬ריבוע ‪ . ADKM‬הוכח כי‬
‫‪M‬‬
‫המשולש ‪ KCE‬הוא משולש שווה‬
‫‪A‬‬
‫‪B‬‬
‫שוקיים וישר ‪-‬זווית‪.‬‬
‫‪)7‬‬
‫א‪.‬‬
‫‪K‬‬
‫‪D‬‬
‫‪C‬‬
‫הוכח‪ :‬אם במשולש התיכון לצלע שווה‬
‫למחצית הצלע אותה הוא חוצה‪,‬‬
‫‪M‬‬
‫אזי המשולש הוא משולש ישר זווית‪.‬‬
‫ב‪.‬‬
‫בציור הנתון‪ RS :‬הוא קטע אמצעים‬
‫‪R‬‬
‫‪S‬‬
‫‪O‬‬
‫במשולש ‪ NO . MNP‬הוא חוצה זווית ‪. MNP‬‬
‫הוכח כי‪. MON  90 :‬‬
‫‪P‬‬
‫‪N‬‬
‫‪ )8‬הוכח כי‪ :‬במשולש ישר זווית‪ ,‬התיכון ליתר שווה למחצית היתר‪.‬‬
‫נסח והוכח את המשפט ההפוך למשפט שבסעיף א‪.‬‬
‫‪ )9‬בטרפז ‪. ( BC AD) ABCD‬‬
‫נתון כי‪ :‬נקודה ‪ E‬נמצאת באמצע אלכסון ‪AC‬‬
‫ונקודה ‪ F‬נמצאת באמצע אלכסון ‪. BD‬‬
‫א‪ .‬הסבר מדוע קטע האמצעים של הטרפז ‪ABCD‬‬
‫עובר דרך הנקודות ‪ E‬ו‪. F -‬‬
‫ב‪ .‬נתון כי‪ . AD  4  EF :‬הוכח כי‪. AD  2  BC :‬‬
‫‪ )11‬נתון מלבן ‪ MNPQ‬שבו ‪. QN  2  NP‬‬
‫אלכסוני המלבן נפגשים בנקודה ‪. O‬‬
‫האריכו את הקטע ‪ MQ‬כאורכו ) ‪. (MQ  QT‬‬
‫א‪ .‬הוכח כי‪. MO  OT :‬‬
‫‪105‬‬
‫‪C‬‬
‫‪B‬‬
‫‪F‬‬
‫‪E‬‬
‫‪D‬‬
‫‪A‬‬
‫‪N‬‬
‫‪M‬‬
‫‪O‬‬
‫‪P‬‬
‫‪Q‬‬
‫‪T‬‬
‫ב‪ .‬הוכח כי‪. OT  PQ :‬‬
‫‪ )11‬במעגל שבציור נתון כי המיתר ‪ AC‬מאונך למיתר ‪. BD‬‬
‫שני המיתרים נחתכים בנקודה ‪. F‬‬
‫דרך הנקודה ‪ F‬מורידים אנך למיתר ‪. AB‬‬
‫המשכו של האנך חותך את המיתר ‪ DC‬בנקודה ‪. E‬‬
‫‪D‬‬
‫‪E‬‬
‫‪A‬‬
‫‪C‬‬
‫‪F‬‬
‫הוכח כי‪. DE  EC :‬‬
‫‪B‬‬
‫‪ )12‬הוכח את המשפט‪ :‬שני משיקים למעגל היוצאים מנקודה אחת‬
‫חיצונית‪ ,‬שווים באורכם‪ AB .‬ו ‪ AC -‬הם שני משיקים למעגל‪.‬‬
‫‪ . AC  a‬נקודה ‪ M‬נמצאת על הקשת ‪. CB‬‬
‫‪ QP‬משיק למעגל בנקודה ‪. M‬‬
‫‪A‬‬
‫הוכח כי‪ :‬היקף המשולש ‪ APQ‬לא תלוי המקומה של‬
‫‪B‬‬
‫‪P‬‬
‫‪M‬‬
‫‪Q‬‬
‫‪C‬‬
‫הנקודה ‪ M‬על הקשת ‪ CB‬והוא גודל קבוע השווה ל‪. 2a -‬‬
‫‪ )13‬טרפז ‪ ( AB DC) ABCD‬חסום במעגל כך שמרכז המעגל ‪ O‬נמצא מחוץ‬
‫לטרפז‪.‬‬
‫נתון כי‪ 9 :‬ס"מ ‪ 21 AB ‬ס"מ ‪ , CD ‬גובה הטרפז הוא ‪ 8‬ס"מ‪B .‬‬
‫רדיוס המעגל הוא ‪. R‬‬
‫‪C‬‬
‫א‪ .‬הבע באמצעות ‪ R‬את המרחק ממרכז המעגל ‪: O‬‬
‫‪ .1‬לבסיס הקטן של הטרפז ‪. AB‬‬
‫‪ .2‬לבסיס הגדול של הטרפז ‪. CD‬‬
‫ב‪ .‬חשב את גודלו של רדיוס המעגל ‪. R‬‬
‫‪A‬‬
‫‪D‬‬
‫‪C‬‬
‫‪ )14‬במשולש ישר זווית ‪ , ( ABC  90 ) ABC‬חוסמים מעגל כך שנקודות‬
‫ההשקה הן‪ P , M :‬ו‪. Q -‬‬
‫‪M‬‬
‫כמו כן‪ ,‬נתון כי‪ AQ  2a :‬ו‪. QC  a -‬‬
‫הבע את היקף המשולש ‪ ABC‬באמצעות ‪. a‬‬
‫‪A‬‬
‫‪106‬‬
‫‪B‬‬
‫‪P‬‬
‫‪Q‬‬
‫‪C‬‬
‫שאלות הכוללות פרופורציה ודמיון‪:‬‬
‫‪ )15‬שני מעגלים משיקים זה לזה בנקודה ‪. M‬‬
‫רדיוס המעגל הגדול הוא ‪ R‬ורדיוס המעגל הקטן הוא ‪. r‬‬
‫מעבירים משיק משותף לשני המעגלים‪.‬‬
‫‪ MN‬הוא המרחק שבין נקודת ההשקה של שני‬
‫המעגלים לבין המשיק המשותף שלהם‪.‬‬
‫‪2R  r‬‬
‫הוכח כי‪:‬‬
‫‪Rr‬‬
‫‪M‬‬
‫‪R‬‬
‫‪r‬‬
‫‪N‬‬
‫‪MN ‬‬
‫‪ )16‬א‪ .‬הוכח כי‪ :‬במשולש ישר זווית בעל זווית חדה בת ‪ , 30‬הניצב שמול‬
‫הזווית שווה למחצית היתר‪.‬‬
‫ב‪ .‬בטרפז שווה שוקיים ‪ ABCD‬האלכסונים ניצבים לשוקיים‪.‬‬
‫הוכח כי‪ :‬אם הזווית החדה בטרפז שווה ל‪ , 60 -‬אזי נקודת מפגש‬
‫האלכסונים מחלקת כל אלכסון ביחס ‪.1: 2‬‬
‫‪ KMN )17‬הוא משולש שווה שוקיים ) ‪ . ( KM  KN‬מנקודה‬
‫כלשהי ‪ P‬הנמצאת על הבסיס ‪ MN‬מורידים אנך לשוק ‪KM‬‬
‫‪K‬‬
‫ואנך לשוק ‪ KN‬החותכים אותן בנקודות ‪ A‬ו‪ B -‬בהתאמה‪.‬‬
‫א‪ .‬הוכח כי ‪ KAPB‬הוא מרובע בר חסימה‪.‬‬
‫ב‪ .‬הסבר מדוע הנקודה ‪ E‬הנמצאת באמצע הבסיס ‪, MN‬‬
‫נמצאת על היקף המעגל החוסם את המרובע ‪. KAPB‬‬
‫‪ )18‬נסח והוכח את משפט קטע אמצעים בטרפז‪.‬‬
‫‪ MN‬הוא קטע אמצעים בטרפז ‪. ( AB CD) ABCD‬‬
‫‪A‬‬
‫‪B‬‬
‫‪N‬‬
‫‪E P‬‬
‫‪C‬‬
‫‪D‬‬
‫‪M‬‬
‫‪N‬‬
‫נסמן‪. CD  b , AB  a :‬‬
‫‪M‬‬
‫‪F‬‬
‫‪E‬‬
‫‪B‬‬
‫‪1‬‬
‫‪2‬‬
‫הוכח כי‪. EF   (a  b) :‬‬
‫‪A‬‬
‫‪ )19‬שני מעגלים שווים‪ O1 ,‬ו ‪ , O2 -‬שמחוגיהם שווים ל ‪ 10 -‬ס"מ‪,‬‬
‫נחתכים בנקודות ‪ A‬ו‪ . B -‬מהנקודה ‪ C‬שעל המשך המיתר‬
‫המשותף ‪ AB‬של שני המעגלים יוצא המשיק ‪ CD‬לאחד‬
‫מהמעגלים‪ .‬נתון כי‪ 9  5 :‬ס"מ ‪ CD ‬ו ‪16 -‬ס"מ ‪. O1O2 ‬‬
‫חשב את אורך הקטע ‪. CB‬‬
‫‪C‬‬
‫‪B‬‬
‫‪D‬‬
‫‪O2‬‬
‫‪O1‬‬
‫‪A‬‬
‫‪107‬‬
‫(היעזר בעובדה ש ‪ AB -‬חוצה את הקטע ‪ O1O2‬ומאונך לו‪).‬‬
‫‪B‬‬
‫‪ C , B , A )21‬ו ‪ D -‬הן נקודות על המעגל‪ K .‬היא נקודה‬
‫על ‪ BC‬כך ש‪ . BK  CD -‬נתון‪. AB  AD :‬‬
‫א‪ .‬הוכח‪. BAK  DAC :‬‬
‫ב‪ .‬המשך הקטע ‪ AK‬חותך את המעגל בנקודה ‪. N‬‬
‫הוכח‪. BN  CD :‬‬
‫‪K‬‬
‫‪A‬‬
‫‪C‬‬
‫‪D‬‬
‫‪M‬‬
‫‪ )21‬במשולש ‪ MNP‬הגבהים ‪ NQ‬ו‪ PR -‬נפגשים בנקודה ‪. O‬‬
‫נתון כי‪. OR  OQ :‬‬
‫א‪ .‬הוכח כי ‪. NO  OP‬‬
‫ב‪ .‬הוכח כי‪ :‬משולש ‪ MNP‬שווה שוקיים‪.‬‬
‫ג‪ .‬הוכח כי‪. MQ  MR :‬‬
‫‪Q‬‬
‫‪R‬‬
‫‪N‬‬
‫‪P‬‬
‫‪ )22‬א‪ .‬הוכח את המשפט‪ :‬שני מיתרים הנחתכים בתוך מעגל מחלקים זה את זה‪,‬‬
‫כך שמכפלת קטעי האחד שווה למכפלת קטעי האחר‪.‬‬
‫ב‪ .‬במעגל שרדיוסו ‪ , R‬הקוטר ‪ AB‬מאונך למיתר ‪. CD‬‬
‫הקוטר והמיתר נחתכים בנקודה ‪ . E‬נתון כי ‪. AE : EB  1: 4‬‬
‫הבע את שטח המשולש ‪ ADC‬באמצעות ‪. R‬‬
‫‪ )23‬א‪ .‬הוכח כי‪ :‬במרובע חסום במעגל‪ ,‬סכום הזוויות הנגדיות שווה ל‪.180 -‬‬
‫ב‪ .‬מרובע ‪ ABCD‬חסום במעגל‪ AC .‬חוצה את הזווית ‪. DAB‬‬
‫בנקודה ‪ C‬מעבירים משיק למעגל‪ .‬המשכי הצלעות ‪ AB‬ו‪AD -‬‬
‫‪A‬‬
‫חותכים את המשיק בנקודות ‪ E‬ו‪ F -‬בהתאמה‪.‬‬
‫‪ .1‬הוכח כי‪. CDF  ABC :‬‬
‫‪ .2‬הוכח כי‪. ABC CDF :‬‬
‫ג‪ .‬נתון ‪ 9‬ס"מ ‪ 4 , AB ‬ס"מ ‪. DF ‬‬
‫חשב את אורך הקטע ‪. BC‬‬
‫‪B‬‬
‫‪E‬‬
‫‪D‬‬
‫‪C‬‬
‫‪F‬‬
‫‪ )24‬מעגל ‪ O‬משיק לישר ‪ l‬בנקודה ‪ CD . E‬הוא קוטר במעגל‪.‬‬
‫בנקודה ‪ C‬מעבירים משיק למעגל החותך את הישר ‪ l‬בנקודה ‪. B‬‬
‫בנקודה ‪ D‬מעבירים משיר למעגל החותך את הישר ‪ l‬בנקודה ‪. A‬‬
‫א‪ .‬הוכח כי‪AOB  90 :‬‬
‫‪108‬‬
‫‪O‬‬
‫‪D‬‬
‫‪C‬‬
‫‪B‬‬
‫‪E‬‬
‫‪A‬‬
‫‪l‬‬
‫ב‪ .‬הוכח כי‪. AOE OBE :‬‬
‫ג‪ .‬נתון כי‪ 6 :‬ס"מ ‪13 , R ‬ס"מ ‪. EB  AE , AB ‬‬
‫חשב את אורכי הקטעים ‪ EB‬ו‪. AE -‬‬
‫‪ )25‬במשולש ‪ ABC‬נתון כי‪ AD :‬הוא התיכון לצלע ‪. BC‬‬
‫‪ DE‬הוא חוצה הזווית ‪ DF , ADB‬הוא חוצה הזווית ‪ADC‬‬
‫‪A‬‬
‫‪F‬‬
‫‪E‬‬
‫(ראה ציור)‪ .‬הוכח כי‪. EF BC :‬‬
‫‪C‬‬
‫‪ )26‬בריבוע ‪ ABCD‬נתון כי‪ :‬אלכסוניו נפגשים בנקודה ‪. M‬‬
‫‪ BE‬חוצה את הזווית ‪ DBA‬וחותך את‬
‫האלכסון ‪ AC‬בנקודה ‪( N‬ראה ציור)‪.‬‬
‫‪DE‬‬
‫‪MN‬‬
‫ואת היחס‬
‫א‪ .‬מצא את היחס‬
‫‪EA‬‬
‫‪NA‬‬
‫‪B‬‬
‫‪D‬‬
‫‪D‬‬
‫‪C‬‬
‫‪M‬‬
‫‪E‬‬
‫‪.‬‬
‫‪N‬‬
‫‪B‬‬
‫ב‪ .‬הוכח כי המשולש‪ ENA :‬הוא משולש שווה שוקיים‪.‬‬
‫ג‪ .‬הוכח כי‪. DE  2  MN :‬‬
‫‪ )27‬במשולש שווה שוקיים ‪ ABC‬נתון כי‪:‬‬
‫‪ 20‬ס"מ ‪ 24 , AC  BC ‬ס"מ ‪. AB ‬‬
‫במשולש זה חסום מעגל‪ ,‬המשיק לשתי השוקיים‬
‫‪A‬‬
‫‪C‬‬
‫‪E‬‬
‫‪F‬‬
‫בנקודות ‪ E‬ו ‪. F -‬‬
‫א‪ .‬הוכח כי‪ EF :‬מקביל לבסיס‪.‬‬
‫ב‪ .‬חשב את אורך הקטע ‪. EF‬‬
‫‪B‬‬
‫‪ )28‬במשולש ישר זווית ‪ ( PST  90) PST‬חסום חצי מעגל‬
‫שמרכזו ‪ O‬נמצא על יתר ‪. PT‬‬
‫א‪ .‬הוכח כי ‪ OS‬חוצה את הזווית ‪. PST‬‬
‫ב‪ .‬נתון כי‪ 18 :‬ס"מ ‪ PS ‬ו‪ 24 -‬ס"מ ‪. TS ‬‬
‫חשב את אורכי הקטעים ‪ OP‬ו‪. OT -‬‬
‫‪A‬‬
‫‪P‬‬
‫‪O‬‬
‫‪N‬‬
‫‪S‬‬
‫‪ )29‬במשולש ‪ , ABC‬בו ‪, B  90‬‬
‫נתון כי‪ 6 :‬ס"מ ‪12 , FC ‬ס"מ ‪16 , BC ‬ס"מ ‪AB ‬‬
‫הקטע ‪ FM‬מאונך ליתר ‪ , AC‬והקטע ‪ MN‬מקביל ליתר ‪. AC‬‬
‫חשב את אורך הקטע ‪. MN‬‬
‫‪T‬‬
‫‪M‬‬
‫‪B‬‬
‫‪M‬‬
‫‪N‬‬
‫‪F‬‬
‫‪A‬‬
‫‪ )31‬משולש ‪ MPN‬חסום במעגל‪ .‬ישר ‪ NQ‬משיק למעגל זה בנקודה ‪. N‬‬
‫נתון כי‪( NP RQ :‬ראה ציור)‪.‬‬
‫‪M‬‬
‫‪109‬‬
‫‪P‬‬
‫‪N‬‬
‫‪R‬‬
‫‪Q‬‬
‫‪C‬‬
‫א‪ .‬הוכח כי‪. QRN MRQ :‬‬
‫ב‪ .‬נתון כי‪ 5 :‬ס"מ ‪ MN ‬ו‪ 4 -‬ס"מ ‪. RN ‬‬
‫חשב את ‪. RQ‬‬
‫‪ )31‬בטרפז ‪. ( AB DC) ABCD‬‬
‫נתון כי‪ 9 :‬ס"מ ‪18 , DC ‬ס"מ ‪. AB ‬‬
‫דרך נקודת מפגש האלכסונים ‪ , E‬מעבירים ישר ‪MN‬‬
‫המקביל לבסיסי הטרפז‪.‬‬
‫מצא את אורכו של ‪. MN‬‬
‫‪D‬‬
‫‪C‬‬
‫‪M‬‬
‫‪N‬‬
‫‪E‬‬
‫‪A‬‬
‫‪B‬‬
‫‪ )32‬א‪ .‬הוכח‪ :‬חוצה זווית במשולש מחלק את הצלע שמול הזווית חלוקה פנימית‬
‫לפי היחס של שתי הצלעות הכולאות את הזווית‪.‬‬
‫ב‪ .‬המעגל החסום במשולש ‪ ABC‬משיק בנקודה ‪ F‬לצלע ‪. CB‬‬
‫‪A‬‬
‫נתון כי‪ 4 :‬ס"מ ‪ 7 BF ‬ס"מ ‪, AD .CF ‬‬
‫חוצה הזווית ‪ A‬מחלק את הקטע ‪ CB‬לשני קטעים‬
‫המתייחסים זה לזה כמו ‪. 3 : 2‬‬
‫חשב את אורכי הצלעות ‪ AC‬ו‪. AB -‬‬
‫‪B‬‬
‫‪D F‬‬
‫‪ )33‬משולש שווה שוקיים ‪ ( AB  AC) ABC‬חסום במעגל‪.‬‬
‫דרך קדקוד ‪ B‬עובר משיק למעגל‪ .‬דרך קדקוד ‪ C‬עובר ישר‬
‫המקביל ל‪ , AB -‬וחותך את משיק בנקודה ‪( E‬ראה ציור)‪.‬‬
‫‪CBE‬‬
‫‪A‬‬
‫‪BAC‬‬
‫א‪ .‬הוכח‪:‬‬
‫ב‪ .‬נתון כי‪ 27 :‬ס"מ ‪ AC ‬ו‪12 -‬ס"מ ‪. CE ‬‬
‫‪ )34‬בטרפז ‪ ( AB CD) ABCD‬נתון כי‪. AB  3  CD :‬‬
‫אלכסוני הטרפז נפגשים בנקודה ‪. O‬‬
‫דרך הנקודה ‪ A‬מעבירים מקביל ל ‪ , BD -‬החותך‬
‫את המשך הצלע ‪ CD‬בנקודה ‪( E‬ראה ציור)‪.‬‬
‫נסמן את שטח המשולש ‪ DOC‬באמצעות ‪. S‬‬
‫הבע את שטח הטרפז ‪ ABCE‬באמצעות ‪. S‬‬
‫‪110‬‬
‫‪C‬‬
‫‪C‬‬
‫‪B‬‬
‫‪E‬‬
‫‪A‬‬
‫‪B‬‬
‫‪O‬‬
‫‪C‬‬
‫‪D‬‬
‫‪E‬‬
‫‪ ABCD )35‬הוא טרפז שווה שוקיים )‪. ( AD  BC , AB CD‬‬
‫‪ O‬הוא מרכז המעגל החסום בטרפז ו ‪ E -‬היא נקודת ההשקה של‬
‫השוק ‪ BC‬עם המעגל ‪( O‬ראה ציור)‪.‬‬
‫א‪ .‬הוכח כי‪. OE 2  BE  EC :‬‬
‫ב‪ .‬הוכח כי‪ :‬הגובה בטרפז שווה שוקיים החוסם מעגל הוא‬
‫הממוצע ההנדסי של שני הבסיסים של הטרפז‪.‬‬
‫‪ )36‬במשולש ישר ‪-‬זווית ‪ ( PQR  90) PQR‬נתון‪:‬‬
‫‪ h‬הוא הגובה ליתר‪ x ,‬ו‪ y -‬הם הניצבים‪,‬‬
‫‪ a‬ו‪ b -‬הם היטלי הניצבים ‪ x‬ו‪ y -‬בהתאמה (ראה ציור)‪.‬‬
‫‪y‬‬
‫א‪ .‬הוכח כי הגובה ליתר הוא ממוצע גאומטרי של‬
‫היטלי הניצבים על היתר‪. h  a  b :‬‬
‫‪R‬‬
‫‪b‬‬
‫‪A‬‬
‫‪B‬‬
‫‪E‬‬
‫‪O‬‬
‫‪D‬‬
‫‪C‬‬
‫‪Q‬‬
‫‪x‬‬
‫‪h‬‬
‫‪N‬‬
‫‪P‬‬
‫‪M‬‬
‫ב‪ .‬הוכח כי כל ניצב הוא ממוצע גאומטרי של היתר‬
‫והיטל הניצב על היתר‪. y  b  (a  b) , x  a  (a  b) :‬‬
‫ג‪.‬‬
‫מקדקוד ‪ Q‬מעבירים חוצה זווית החותך את היתר ‪ PR‬בנקודה ‪. M‬‬
‫הוכח כי‪. PM : MR  a : b :‬‬
‫‪ )37‬במשולש ‪ ABC‬התיכון ‪ BE‬והקטע ‪ AL‬נחתכים בנקודה ‪. K‬‬
‫הקטע ‪ EF‬מקביל ל ‪( AL -‬ראה ציור)‪ .‬נתון כי‪. LC  5  BL :‬‬
‫א‪ .‬הוכח כי‪. LF  2.5  BL :‬‬
‫ב‪.‬‬
‫‪BK 2‬‬
‫הוכח כי‪ :‬‬
‫‪BE 7‬‬
‫‪A‬‬
‫‪E‬‬
‫‪K‬‬
‫‪.‬‬
‫‪C‬‬
‫‪F‬‬
‫‪L‬‬
‫‪ )38‬א‪ .‬הוכח את המשפט‪ :‬היחס בין השטחים של שני משולשים דומים שווה‬
‫לריבוע יחס הדימיון‪.‬‬
‫‪G‬‬
‫ב‪ .‬במקבילית ‪ ABCD‬נקודה ‪ E‬נמצאת על‬
‫הצלע ‪ , BC‬כך ש‪. BE : CE  2 : 3 -‬‬
‫המשך הקטע ‪ AE‬חותך את המשך הצלע ‪DC‬‬
‫‪E‬‬
‫בנקודה ‪ . G‬נתון ‪18‬סמ"ר ‪. SCEG ‬‬
‫‪C‬‬
‫‪ .1‬חשב את שטח המשולש ‪. ABE‬‬
‫‪ .2‬חשב את שטח המשולש ‪. ABC‬‬
‫‪B‬‬
‫‪B‬‬
‫‪A‬‬
‫‪D‬‬
‫‪ )39‬א‪ .‬הוכח כי‪ :‬במשולשים דומים היחס בין הגבהים המתאימים‬
‫שווה ליחס הדמיון של המשולשים‪.‬‬
‫‪C‬‬
‫‪111‬‬
‫‪Q‬‬
‫‪B‬‬
‫‪E‬‬
‫‪P‬‬
‫‪D‬‬
‫‪A‬‬
‫ב‪ .‬במשולש ‪ ABC‬חסום חצי מעגל שרדיוסו ‪ 6‬ס"מ‪.‬‬
‫קוטר המעגל ‪ PQ‬מקביל לצלע ‪ CD . AB‬הוא גובה במשולש‬
‫‪ ABC‬וחותך את הקוטר ‪ PQ‬בנקודה ‪( E‬ראה ציור)‪.‬‬
‫נתון כי‪ 20 :‬ס"מ ‪. AB ‬‬
‫חשב את אורך הקטע ‪. CE‬‬
‫‪112‬‬
‫‪ ABCD )41‬הוא טרפז )‪ . ( BC AD‬הצלעות ‪ BC‬ו ‪ CD -‬הן מיתרים במעגל‪.‬‬
‫הצלע ‪ AB‬משיקה למעגל בנקודה ‪( B‬ראה ציור)‪.‬‬
‫‪C‬‬
‫א‪ .‬הוכח כי‪. ABD DCB :‬‬
‫ב‪ .‬נתון כי‪ 5 :‬ס"מ ‪12.8 , BC ‬ס"מ ‪. AD ‬‬
‫חשב את אורך האלכסון ‪. BD‬‬
‫‪D‬‬
‫‪ )41‬מנקודה ‪ A‬הנמצאת מחוץ למעגל שרדיוסו ‪ , R‬מעבירים חותך‬
‫וחותך ‪ , AOD‬שעובר דרך מרכז המעגל ‪, O‬‬
‫כך ש ‪. CDB  BDA  BAD   -‬‬
‫נתון גם‪. BC  n , AB  m :‬‬
‫‪A‬‬
‫‪B‬‬
‫‪A‬‬
‫‪ABC‬‬
‫‪C‬‬
‫‪B‬‬
‫‪O‬‬
‫הוכח כי‪. DC 2  n2  m  n :‬‬
‫‪ )42‬א‪ .‬הוכח כי‪ :‬חותכים למעגל היוצאים מנקודה אחת מחוץ למעגל‬
‫יוצרים קטעים פרופורציוניים כך שמכפלת כל החותך בחלקו‬
‫מחוץ למעגל היא גודל קבוע‪.‬‬
‫‪A‬‬
‫ב‪ .‬נתון משולש ‪ . ABC‬מעגל העובר דרך הקדקודים ‪ A‬ו‪, B -‬‬
‫חותך הצלעות ‪ AC‬ו ‪ BC -‬בנקודות ‪ F‬ו‪ M -‬בהתאמה‪.‬‬
‫‪F‬‬
‫‪ .1‬הוכח כי‪. ACM BCF :‬‬
‫‪ .2‬נתון כי‪ 48 :‬ס"מ ‪ 40 , BC ‬ס"מ ‪, AC ‬‬
‫‪C‬‬
‫‪16‬ס"מ ‪ . AF ‬מצא את אורך המיתר ‪. BM‬‬
‫‪ )43‬בטרפז ‪ ABCD‬אורך הבסיס ‪ AB‬הוא ‪ a‬ואורך הבסיס ‪ CD‬הוא ‪.b‬‬
‫אלכסוני הטרפז נפגשים בנקודה ‪. O‬‬
‫דרך הנקודה ‪ O‬מעבירים מקביל לבסיסים החותך‬
‫את ‪ AD‬בנקודה ‪ E‬ואת ‪ BC‬בנקודה ‪. F‬‬
‫‪a b‬‬
‫הוכח כי מתקיים‪:‬‬
‫‪ab‬‬
‫‪. EO  OF ‬‬
‫‪B‬‬
‫‪M‬‬
‫‪B‬‬
‫‪F‬‬
‫‪C‬‬
‫‪113‬‬
‫‪A‬‬
‫‪a‬‬
‫‪A‬‬
‫‪E‬‬
‫‪O‬‬
‫‪b‬‬
‫‪ )44‬מנקודה ‪ A‬מעבירים שני חותכים למעגל‪ ,‬חותך ‪ ABC‬וחותך ‪, ADE‬‬
‫כך שהנקודה ‪ B‬נמצאת באמצע הקשת ‪ , CD‬ו ‪CED  2 CAD -‬‬
‫(ראה ציור)‪.‬‬
‫‪B‬‬
‫א‪ .‬הוכח‪. ECB ACE :‬‬
‫ב‪ .‬נתון כי‪ 4 :‬ס"מ ‪ 9 ,CB ‬ס"מ ‪. AC ‬‬
‫חשב את אורך הקטע ‪. CE‬‬
‫‪D‬‬
‫‪D‬‬
‫‪D‬‬
‫‪C‬‬
‫‪E‬‬
‫‪ MN )45‬הוא קטע במעגל שמרכזו ב‪. O -‬‬
‫‪ PK‬משיק למעגל בנקודה ‪ P‬ומאונך ל‪. NQ -‬‬
‫‪Q‬‬
‫‪P‬‬
‫הנקודה ‪ Q‬נמצאת על המשך המיתר ‪( MP‬ראה ציור)‪.‬‬
‫‪K‬‬
‫‪N‬‬
‫א‪ .‬הוכח כי‪. MP  KN  PK  PN :‬‬
‫ב‪ .‬הוכח כי‪. MP  PQ :‬‬
‫‪O‬‬
‫‪C‬‬
‫‪A‬‬
‫‪ )46‬בציור נתון כי‪. AB EF CD :‬‬
‫‪1‬‬
‫‪1‬‬
‫‪1‬‬
‫‪‬‬
‫‪‬‬
‫הוכח כי‪:‬‬
‫‪EF AB CD‬‬
‫‪M‬‬
‫‪E‬‬
‫‪.‬‬
‫‪D‬‬
‫‪F‬‬
‫‪A‬‬
‫‪ )47‬א‪ .‬הוכח כי‪ :‬הגובה ליתר במשולש ישר‪-‬זווית מחלק את המשולש‬
‫לשני משולשים‪ ,‬שכל אחד מהם דומה למשלוש כולו‪.‬‬
‫‪T‬‬
‫ב‪ .‬מעויין ‪ ABCD‬חוסם מעגל שמרכזו ב ‪. O -‬‬
‫נתון כי‪ :‬אורך הרדיוס המעגל ‪ OT‬הוא ‪ 24‬ס"מ‬
‫‪B‬‬
‫‪D‬‬
‫‪B‬‬
‫‪O‬‬
‫ואורך צלע המעויין הוא ‪ 50‬ס"מ‪.‬‬
‫מצא את אורך האלכסון ‪. ( BD  AC ) BD‬‬
‫‪C‬‬
‫‪ )48‬משולש ‪ ABC‬חסום במעגל‪ .‬חוצה זווית ‪ BAC‬חותך‬
‫את המעגל בנקודה ‪ D‬ואת הצלע ‪ BC‬בנקודה ‪( F‬ראה ציור)‪.‬‬
‫מנקודה ‪ D‬הורד אנך על הצלע ‪ CB‬החותך אותה‬
‫בנקודה ‪ . E‬נתון כי‪. AB : AC  5 : 3 :‬‬
‫הוכח כי‪. BC  8  EF :‬‬
‫‪C‬‬
‫‪A‬‬
‫‪E‬‬
‫‪B‬‬
‫‪F‬‬
‫‪D‬‬
‫‪ )49‬נקודה ‪ D‬היא אמצע היתר ‪ AC‬המשולש ישר זווית ‪. ( B  90) ABC‬‬
‫בנקודה ‪ D‬מעלים אנך לצלע ‪ AC‬החותך את הניצב ‪ AB‬בנקודה ‪E‬‬
‫(ראה ציור)‪.‬‬
‫נתון כי‪ 8 :‬ס"מ ‪. AB  m , AC ‬‬
‫‪D‬‬
‫הבע את ‪ CE‬ו‪ BE -‬באמצעות ‪. m‬‬
‫‪A‬‬
‫‪E‬‬
‫‪C‬‬
‫‪114‬‬
‫‪B‬‬
‫‪ )51‬במשולש ‪ ABC‬נתון כי‪15 :‬ס"מ ‪, AB  AC ‬‬
‫‪18‬ס"מ ‪ . CB ‬דרך מרכז המעגל ‪ O‬החסום במשולש‬
‫עובר הקטע ‪ EF‬המקביל לבסיס ‪ FN . BC‬ו‪EM -‬‬
‫‪A‬‬
‫‪O‬‬
‫‪F‬‬
‫‪E‬‬
‫הם אנכים לבסיס ‪. BC‬‬
‫חשב את שטח המלבן ‪. EFNM‬‬
‫‪B‬‬
‫‪N‬‬
‫‪C‬‬
‫‪M‬‬
‫‪ )51‬א‪ .‬הוכח כי‪ :‬הזווית הכלואה בין משיק ומיתר בעלי נקודה משותפת‪,‬‬
‫שווה לזווית ההיקפית הנשענת על מיתר זה‪.‬‬
‫‪E‬‬
‫ב‪ .‬שני מעגלים משיקים מבחוץ בנקודה ‪. A‬‬
‫‪F‬‬
‫דרך נקודה זו עוברים שני ישרים‪ ,‬החותכים‬
‫‪A‬‬
‫‪M‬‬
‫את המעגלים בנקודות ‪ M , E , F‬ו ‪. N -‬‬
‫הוכח כי‪. AMN AFE :‬‬
‫‪N‬‬
‫‪E‬‬
‫‪ )52‬במשולש ישר ‪-‬זווית ‪, ( GEF  90) EFG‬‬
‫‪ EP‬הוא הגובה ליתר ‪. GF‬‬
‫נתון כי‪ 24 :‬ס"מ ‪ 32 , EF ‬ס"מ ‪. GE ‬‬
‫‪F‬‬
‫חשב את אורכי הקטעים‪ GP , PF , GF :‬ו‪. EP -‬‬
‫‪P‬‬
‫‪G‬‬
‫‪ MQ )53‬הוא התיכון לבסיס במשולש שווה שוקיים ‪. (MN  MP) MNP‬‬
‫‪ S‬היא נקודה על המשך הצלע ‪. MN‬‬
‫‪M‬‬
‫המשך התיכון ‪ MQ‬חותך את הקטע ‪ PS‬בנקודה ‪. E‬‬
‫הקטע ‪ EF‬מקביל ל ‪( NP -‬ראה ציור)‪.‬‬
‫א‪ .‬הוכח כי‪. MP : MS  NF : FS :‬‬
‫ב‪ .‬נתון כי‪ 20 :‬ס"מ ‪ 4 , MP ‬ס"מ ‪. NF ‬‬
‫חשב את אורך הקטע ‪. FS‬‬
‫‪P‬‬
‫‪M‬‬
‫‪Q‬‬
‫‪E‬‬
‫‪N‬‬
‫‪F‬‬
‫‪S‬‬
‫‪115‬‬
‫‪N‬‬
‫‪M‬‬
‫‪ NP )54‬הוא קוטר במעגל ‪ , MT , MN . O‬ו‪ SP -‬הם‬
‫משיקים למעגל ‪ O‬בנקודות ‪ T , N‬ו‪ P -‬בהתאמה‪.‬‬
‫א‪ .‬הוכח כי‪. MOS  90 :‬‬
‫ב‪ .‬הוכח כי רדיוס המעגל שווה ל‪. MN  SP -‬‬
‫‪T‬‬
‫‪O‬‬
‫‪S‬‬
‫‪P‬‬
‫‪ DE )55‬הוא קוטר במעגל‪ .‬בנקודה ‪ D‬מעבירים משיק למעגל‪.‬‬
‫מנקודה ‪ , A‬שעל המעגל‪ ,‬מעבירים ישר המקביל לקוטר ‪. DE‬‬
‫הישר חותך את המשיק למעגל בנקודה ‪( F‬ראה ציור)‪.‬‬
‫א‪ .‬הוכח כי‪. AD2  AF  DE :‬‬
‫‪E‬‬
‫ב‪ .‬נתון ‪ 4‬ס"מ ‪ 9 , AF ‬ס"מ ‪. DE ‬‬
‫חשב את שטח הטרפז ‪. AFDE‬‬
‫‪A‬‬
‫‪D‬‬
‫‪N‬‬
‫‪ )56‬א‪ .‬הוכח כי המחוג המאונך למיתר המעגל חוצה אותו‪.‬‬
‫ב‪ .‬בציור שלפניך המיתרים ‪ EF‬ו‪ MN -‬מאונכים זה לזה‪.‬‬
‫‪O‬‬
‫נתון כי‪ 3 :‬ס"מ ‪8 , EB ‬ס"מ ‪ 4 , BF ‬ס"מ ‪. MB ‬‬
‫‪ .1‬חשב את אורך הקטע ‪. NB‬‬
‫‪ .2‬מצא את המרחק המיתר ‪ EF‬ממרכז המעגל ‪. O‬‬
‫‪F‬‬
‫‪F‬‬
‫‪A‬‬
‫‪B‬‬
‫‪E‬‬
‫‪M‬‬
‫‪C‬‬
‫‪ )57‬מעגל שמרכזו בנקודה ‪ O‬חסום במשולש ישר‪-‬זווית )‪. ( C  90‬‬
‫‪E‬‬
‫נתון כי‪ 30 :‬ס"מ ‪18 , AB ‬ס"מ ‪. AC ‬‬
‫‪D‬‬
‫חשב את אורך הקטע ‪. ED‬‬
‫‪O‬‬
‫‪A‬‬
‫‪B‬‬
‫‪ )58‬במשולש ‪ PS MPQ‬חוצה את הזווית ‪. ST MP , MPQ‬‬
‫נתון כי‪ 27 :‬ס"מ ‪ 45 , MP ‬ס"מ ‪. QP ‬‬
‫חשב את אורך הקטע ‪. TP‬‬
‫‪M‬‬
‫‪S‬‬
‫‪P‬‬
‫‪T‬‬
‫‪Q‬‬
‫‪116‬‬
1
3
.  3  a 2 :‫ שטח המשולש‬,
. a  (3  17) )14 . R  ‫ ס"מ‬10.625 .‫ב‬
. BC  ‫ ס"מ‬6 .‫) ג‬23
2
 3  a :‫ אורך צלע המשולש‬.‫) ב‬3
3
R 2  10.52 .2
. SACD 
8
25
R 2  4.52 .1 .‫) א‬13
R 2 .‫) ב‬22 . CB  ‫ ס"מ‬15 )19
MN
2
DE

,
 2 .‫) א‬26 . AE  ‫ ס"מ‬9 , EB  ‫ ס"מ‬4 .‫) ג‬24
NA
2
EA
OT 
‫ס"מ‬
120
90
, OP  ‫ס"מ‬
.‫) ב‬28 . EF  ‫ ס"מ‬9.6 .‫) ב‬27
7
7
. MN  ‫ ס"מ‬12 )31
1
. RQ  ‫ ס"מ‬6 .‫) ב‬31 . MN  ‫ ס"מ‬3 )29
3
. AC  ‫ ס"מ‬9 , AB  ‫ ס"מ‬6 .‫) ב‬32
. S ABCE  28  S )34 . BC  ‫ ס"מ‬18 .‫) ב‬33
.CE  ‫ ס"מ‬9 .‫) ב‬39 . SABC  ‫ סמ"ר‬20 .2 SABE  ‫ סמ"ר‬8 .1 .‫) ב‬38
. CE  ‫ ס"מ‬6 .‫) ב‬44 . BM  ‫ ס"מ‬28 .‫) ב‬42
. BD  ‫ ס"מ‬8 .‫) ב‬41
m2  32
32
, CE 
)49
m
m
. BD  ‫ ס"מ‬60 .‫) ב‬47
. BE 
. SEFNM  ‫ סמ"ר‬50.625 )51
. EP  ‫ ס"מ‬19.2 , GP  ‫ ס"מ‬25.6 , PF  ‫ ס"מ‬14.4 , GF  ‫ ס"מ‬40 )52
. S AFDE  ‫ סמ"ר‬29.07 .‫) ב‬55 . FS  ‫ ס"מ‬6 .‫) ב‬53
.TP = ‫ ס"מ‬16.875 )58 .DE = ‫ ס"מ‬3 )57 .‫ ס"מ‬1 .2
117
NB  ‫ ס"מ‬6 .1 .‫) ב‬56
‫פרק ‪ – 5‬טריגונומטריה במישור‪:‬‬
‫משולש ישר זווית‪:‬‬
‫הגדרות הפונקציות הטריגונומטריות‪:‬‬
‫הניצב שמול הזווית‬
‫היתר‬
‫הניצב שליד הזווית‬
‫היתר‬
‫הניצב שמול הזווית‬
‫הניצב שליד הזווית‬
‫משפט פיתגורס‪. a2  b2  c2 :‬‬
‫‪ )1‬מצא את ערכו של ‪  / x‬במשולשים ישרי הזווית הבאים‪:‬‬
‫‪750‬‬
‫‪400‬‬
‫‪700‬‬
‫‪A‬‬
‫‪ )2‬המשולש ‪ ABC‬שבציור הוא משולש ישר זווית ( ‪.) B  90o‬‬
‫‪ AD‬הוא התיכון לניצב ‪. BC‬‬
‫נתון‪. AB  6cm , C  28o :‬‬
‫מצא‪. AD  ? , BAD  ? :‬‬
‫‪C‬‬
‫‪ BD‬הוא התיכון ליתר ו‪ AE -‬הוא חוצה הזווית ‪. A‬‬
‫נתון‪. BC  8cm , BD  5.6cm :‬‬
‫מצא‪. BE  ? , BAE  ? :‬‬
‫‪118‬‬
‫‪C‬‬
‫‪B‬‬
‫‪D‬‬
‫‪A‬‬
‫‪D‬‬
‫‪E‬‬
‫‪B‬‬
‫‪ )4‬מצא את זויותיו של מעויין שאורכי אלכסוניו ‪ 24‬ס"מ ו ‪ 18-‬ס"מ‪.‬‬
‫‪D‬‬
‫‪A‬‬
‫‪ )5‬המשולש ‪ ABC‬חסום במעגל כך שהצלע ‪ AC‬היא קוטר המעגל‪.‬‬
‫המשיק למעגל בנקודה ‪ A‬והמשך הצלע ‪ CB‬נפגשים בנקודה ‪. D‬‬
‫נתון‪. DAB  32o , BD  4cm :‬‬
‫מצא את אורכו של רדיוס המעגל‪.‬‬
‫‪B‬‬
‫‪C‬‬
‫‪ )6‬במשולש שווה שוקיים שבו השוק ארוכה ב‪ 4 -‬ס"מ מהבסיס נתון כי זווית הראש‬
‫היא ‪ . 34.92o‬מצא את שטח המשולש‪.‬‬
‫‪A‬‬
‫נתון‪. AB  a , A   :‬‬
‫הבע באמצעות ‪ ‬ו‪ a -‬את היקף המשולש‪.‬‬
‫‪C‬‬
‫‪B‬‬
‫‪A‬‬
‫‪ AD‬הוא התיכון לניצב ‪. BC‬‬
‫נתון‪. AB  b , C   :‬‬
‫הבע באמצעות ‪ ‬ו‪ b -‬את אורכי הקטעים ‪ BD‬ו ‪. AD -‬‬
‫‪C‬‬
‫‪B‬‬
‫‪D‬‬
‫‪ )9‬במשולש ישר זווית אחת הזוויות החדות היא ‪ ‬ואורך חוצה זווית זו הוא ‪. k‬‬
‫הבע באמצעות ‪ ‬ו‪ k -‬את שטח המשולש ואת אורך היתר‪.‬‬
‫‪ )11‬טרפז ‪ ABCD‬הוא טרפז ישר זווית ( ‪.) B  C  90o‬‬
‫הנקודה ‪ G‬נמצאת על השוק ‪ BC‬כך ש‪. AG  DG -‬‬
‫נתון‪. BAG   , AG  DG  m :‬‬
‫הבע באמצעות ‪ ‬ו‪ m -‬את שטח הטרפז‪.‬‬
‫‪ )11‬המשולש ‪ ABC‬הוא ישר זווית ‪.  A  90‬‬
‫הקטעים ‪ AD‬ו‪ AE-‬הם בהתאמה גובה ליתר וחוצה זווית‪.‬‬
‫מסמנים‪. DAE   , DE  k :‬‬
‫א‪ .‬הבע באמצעות ‪ k‬ו‪  -‬את שטח המשולש ‪.ABC‬‬
‫ב‪ .‬חשב את שטח המשולש ‪ABC‬‬
‫אם ידוע כי‪   30 :‬ו ‪. k  2 -‬‬
‫‪119‬‬
‫‪B‬‬
‫‪A‬‬
‫‪G‬‬
‫‪C‬‬
‫‪D‬‬
120
‫‪ )12‬במלבן ‪ ABCD‬מסמנים את הנקודות ‪ E‬ו ‪ F-‬הנמצאות‬
‫על הצלעות ‪ AB‬ו‪ BC-‬בהתאמה כך ש‪E-‬‬
‫מקיימת‪ 3AE  BE :‬ו ‪ F-‬היא אמצע הצלע ‪.BC‬‬
‫אורך הצלע ‪ AD‬שווה לאורך הקטע ‪.BE‬‬
‫מעבירים את הקטעים ‪ DF , EF‬ו‪ DE-‬כך‬
‫שנוצר במשולש ‪.DEF‬‬
‫א‪ .‬סמן ב‪ t -‬את אורך הקטע ‪ AE‬והבע באמצעות ‪t‬‬
‫את אורכי צלעות המשולש ‪.DEF‬‬
‫ב‪ .‬חשב את זוויות המשולש ‪.EDF‬‬
‫‪ )13‬משולש שווה שוקיים שאורך שוקו ‪ k‬וזווית הבסיס שלו היא ‪ ‬חוסם מעגל‪.‬‬
‫הבע באמצעות ‪ ‬ו‪ k -‬את רדיוס המעגל‪.‬‬
‫‪ )14‬בטרפז ישר זווית חסום מעגל‪ .‬אורך השוק הארוכה בטרפז היא ‪ b‬והזווית שהיא‬
‫יוצרת עם הבסיס הגדול היא ‪ .‬הבע באמצעות ‪ ‬ו‪ b -‬את אורכו של הבסיס‬
‫הגדול בטרפז ואת שטחו‪.‬‬
‫* הערה‪ :‬השאלות הבאות משלבות ידע בגיאומטריה ובטריגונומטריה יחד‪:‬‬
‫‪ )15‬דרך הקדקודים ‪ C , A‬ו‪ D-‬של המקבילית ‪ABCD‬‬
‫מעבירים מעגל‪ .‬היקף המעגל חוצה את הצלע ‪AB‬‬
‫בנקודה ‪ .(AE=BE) E‬נתון כי ‪ DC‬הוא קוטר במעגל‬
‫וכי המיתר ‪ DE‬חוצה את זווית ‪.D‬‬
‫א‪ .‬הוכח כי המיתר ‪ CE‬חוצה את זוויות ‪.C‬‬
‫ב‪ .‬רדיוס המעגל יסומן ב‪. R -‬הבע באמצעות ‪ R‬את היקף המקבילית‪.‬‬
‫ג‪ .‬מצא את רדיוס המעגל אם ידוע כי שטח המקבילית הוא ‪ 16 3‬סמ"ר‪.‬‬
‫‪ )16‬מהנקודה ‪ A‬שמחוץ למעגל מעבירים משיק ‪ AB‬וישר חותך ‪.ACD‬‬
‫מעבירים את המיתרים השווים ‪ BC‬ו ‪ .BE-‬כמוכן מעבירים‬
‫את המיתר ‪ .DE‬אורך המיתר ‪ CE‬שונה מאורך המשיק ‪.AB‬‬
‫א‪ .‬הוכח כי המרובע ‪ ABEC‬הוא טרפז‪.‬‬
‫ב‪ .‬הוכח כי‪. 2  BEC  EDC :‬‬
‫ג‪ .‬איזה מרובע יהיה המרובע ‪BEDC‬‬
‫אם יתקיים‪? EDC  90 :‬‬
‫ד‪ .‬נתונים‪ 6 , A  40 :‬ס"מ = ‪ 9 ,AC‬ס"מ = ‪ 8 , AB‬ס"מ = ‪.CE‬‬
‫‪121‬‬
.ABEC ‫חשב את שטח המרובע‬
.  29.745 .‫ ה‬  40.005 .‫ ד‬x  3.931cm .‫ ג‬x  8.114cm .‫ ב‬x  15.665cm .‫) א‬1
. BE  3.294cm , BAE  22.792 )3 AD  8.236cm , BAD  43.24 )2
. S  28.618cm )6 R  6.04cm )5 73.74, 73.74, 106.26, 106.26 )4
2
. AD  b2 
b2
4 tan 2 
b
2 tan 
, BD 

)8 P  a 1  tan  


1 
 )7
cos  

tan 
2
)9
cos 
2
2
m sin   m cos  

k2
.‫ סמ"ר‬24 .‫ ב‬S 
.‫) א‬11
)11
2
cos 2 tan 2 
. 81.86 , 51 , 47.14 .‫ ב‬DE  t 10 , EF  t 11.25 , DF  t 18.25 .‫) א‬12
1
b sin 
1
1

, S  b2 sin  1  sin   )14 R  k cos  tan )13
b sin   2

2
2
2
tan
2
.‫ סמ"ר‬34.43 .‫ ד‬.‫ ריבוע‬.‫) ג‬16 .‫ ס"מ‬4 .‫ ג‬6R .‫) ב‬15
. AC 
k cos
2
,S 
k 2 cos 2
:‫זהויות טריגונומטריות‬
:‫זהויות של סכום והפרש זוויות‬
:‫זהויות היסוד‬
:‫זהויות של זווית כפולה‬
:‫המעגל הטריגונומטרי‬
‫המעגל הטריגונומטרי הוא מעגל היחידה‬
.)1 ‫(מעגל קנוני שרדיוסו‬
122
:‫טבלת ערכי הפונקציות הטריגונומטריות לזוויות המיוחדות‬

0
sin 
cos 

0  


1  

45
60
0

2 
30
1 
1
 

2  2 
2
2
3
2
4

2 
3
2
2
2
1
2

1
 

 2 
90

1  


0  

tan 
0
3
3
1
3

cot 

3
1
3
3
0
4

2 
0

2 
: 90 ‫ערכים עבור זוויות בכפולות של‬
sin 0o  0
cos 0o  1
tan 0o  0
sin 90o  1
cos 90o  0
tan 90o  
sin180o  0
cos180o  1
tan180o  0
sin 270o  1
cos 270o  0
tan 270o  
:‫הזהויות של המעגל הטריגונומטרי‬
tan 180o      tan 
cos 180o      cos 
sin 180o     sin 
tan 180o     tan 
cos 180o      cos 
sin 180o      sin 
tan      tan 
cos     cos 
sin      sin 
123
:‫שאלות‬
:‫) הוכח את הזהויות הבאות‬1
sin 
 tan 
sin  90     cos3 
3
o
tan 2   sin 2   tan 2  sin 2 
cos3   cos  sin 2   cos 
.‫ב‬
sin 2 
sin 2 

2
1  cos  1  cos 
.‫ד‬
. tan   tan  
sin    
cos  cos 
.‫א‬
.‫ג‬
:‫) הוכח את הזהות הבאה‬2
:‫) הוכח את הזהויות הבאות‬3
4sin  cos  cos 2  sin 4
 sin 3  cos3 
 sin   cos  
.‫ב‬
2
 1  sin 2
.‫א‬
 1  sin 6
.‫ד‬
cos4   sin 4   cos 2
.‫ג‬
cos  sin 

 2cot 2
sin  cos 
.‫ו‬
cos 2  2sin 2  cos 2 1
 cot 2
sin 4
2
.‫ה‬
2
:‫) ענה בלי להשתמש במחשבון‬4
cos  45o  
tan 225o 
sin150o 
sin 510o 
cos930o 
sin 315o 
cos120o 
cos 210o 
tan120o 
tan  225o  
.
tan  30o  
sin 180o     sin  90o   
cos  2 

sin 330o 
1
:‫) הוכח את הזהות הבאה‬5
cos   sin 
124
‫משוואות טריגונומטריות‪:‬‬
‫תזכורת – פתרון כללי של משוואה טריגונומטרית‪:‬‬
‫פתרון כללי של המשוואה‪ sin x  sin  :‬הוא מהצורה‪. x1    2 k , x2      2 k :‬‬
‫פתרון כללי של המשוואה‪ cos x  cos :‬הוא מהצורה‪. x1,2    2 k :‬‬
‫פתרון כללי של המשוואה‪ tan x  tan  :‬הוא מהצורה‪. x     k :‬‬
‫‪ )1‬פתור את המשוואות הבאות בתחום המצוין לידן‪:‬‬
‫‪1‬‬
‫א‪.‬‬
‫‪2‬‬
‫ג‪.‬‬
‫‪3‬‬
‫‪2‬‬
‫‪1‬‬
‫ה‪.‬‬
‫‪2‬‬
‫ז‪.‬‬
‫‪0  x  2 : sin x ‬‬
‫‪0  x  2 : sin x  ‬‬
‫‪0  x  2 : cos x ‬‬
‫‪1‬‬
‫‪3‬‬
‫‪0  x  2 : tan x ‬‬
‫‪2‬‬
‫ב‪.‬‬
‫‪2‬‬
‫‪1‬‬
‫ד‪.‬‬
‫‪2‬‬
‫ו‪.‬‬
‫‪0  x  2 : sin x ‬‬
‫‪0  x  2 : sin x  ‬‬
‫‪3‬‬
‫‪2‬‬
‫‪0  x  2 : cos x  ‬‬
‫ח‪0  x  2 : tan x  1 .‬‬
‫ט‪0  x  2 : sin x  0.7 .‬‬
‫י‪0  x  2 : cosx  0.6 .‬‬
‫יא‪0  x  2 : tan x  5 .‬‬
‫יב‪0  x  2 : sin x  1.85 .‬‬
‫‪ )2‬פתור את המשוואות הבאות בתחום המצוין לידן‪:‬‬
‫א‪0  x   : 2sin 3x  1 .‬‬
‫ב‪0  x   : 2cos 2 x   3 .‬‬
‫ג‪0  x  0.25 : tan5x  1 .‬‬
‫ד‪0  x   : 3sin 2 x  2 .‬‬
‫ה‪0  x   : 3cos3x  1 .‬‬
‫ו‪0  x  0.5 : 2 tan 4 x  1 .‬‬
‫‪125‬‬
:‫) פתור את המשוואות הבאות בתחום המצוין לידן‬3
0  x  2 : sin x  1 .‫ב‬
0  x  2 : sin x  0 .‫א‬
0  x  2 : cos x  0 .‫ד‬
0  x  2 : sin x  1 .‫ג‬
0  x  2 : cos x  1 .‫ו‬
0  x  2 : cos x  1 .‫ה‬
0  x  2 : tan x  1 .‫ח‬
0  x  2 : tan x  0 .‫ז‬
:)‫) פתור את המשוואות הבאות בתחום המצוין לידן (זווית מורכבת‬4
2
 5

0  x   : cos 
 3x  
.‫ב‬
 12
 2

3

0  x  2 : sin  2 x    
.‫א‬
6
2



0  x   : sin 2 x  sin  x   .‫ד‬
6

 5

0  x   : tan 
 x   1.3 .‫ג‬
 18

0 x
 2

0  x  2 : sin x  sin 
 x  .‫ה‬
 3




: tan2 x  tan   x  .‫ו‬
2
3


: sin x  sin 3x .‫ח‬
4

0  x  2 : cos x  cos    x  .‫ז‬
 18

0  x   : tan x  tan 3x .‫י‬
0  x  2 : cosx  cos3x .‫ט‬
0 x
2
:)‫) פתור את המשוואות הבאות בתחום המצוין לידן (טכניקה אלגברית‬5
0  x   : sin 2 x 
1
.‫ב‬
4
0  x   : cos 2 x 
3
.‫א‬
4
0  x   : sin x cos3x  0 .‫ד‬
0  x  0.5 : tan 2 2 x  3 .‫ג‬
0  x   : 2cos2 x  3 cos x  0 .‫ו‬
0  x   : sin 2 x  2sin 2 2 x  0 .‫ה‬
0  x  2 : 3sin 2 x  sin x  2 .‫ח‬
0  x  2 : 2sin 2 x  sin x  1  0 .‫ז‬
0  x  2 : cos2 x  2cos x  3
.‫י‬
0  x  2 : 6sin 2 x  sin x  1  0 .‫ט‬
0  x   : tan 2 x  4 tan x 1 .‫יב‬
0  x  2 : tan 2 x  3tan x  4  0 .‫יא‬
126
:)‫) פתור את המשוואות הבאות בתחום המצוין לידן (שימוש בזהויות יסוד‬6
0  x  2 : 2cos2 x  3sin x .‫ב‬
2
0  x  2 : cos x  sin 2 x .‫א‬
3
0  x  2 : cos2 x  sin 2 x  sin x .‫ד‬
0  x  2 : sin 2 x  cos x 
1
4
.‫ג‬
.‫ו‬
0  x   : sin 2 x  2cos2 x  1.5 .‫ה‬
0  x  2 : sin x  tan x  0 .‫ח‬
0  x  2 : tan x  2sin x .‫ז‬
0  x   : 2sin 2 x  3cos 2 x 
3
4


0  x   : sin  2 x    cos x
3

.‫י‬


0  x  2 : sin x  cos  x   .‫ט‬
4

0  x   : cos x  sin  0.9  3x  .‫יב‬
0 : 2 : cos  x-0.3   sin  0.4 -x  .‫יא‬
: cos x -‫) פתור את המשוואות הבאות ע"י חלוקה ב‬7
0  x  2 : sin x   cos x .‫ב‬
0  x  2 : sin x  cos x .‫א‬
0  x  2 : 3sin x  cos x .‫ד‬
0  x  2 : sin x  2cos x .‫ג‬
.‫ו‬
0  x  2 : 4sin x  7cos x .‫ה‬
0  x   : 3sin 2 x  cos2 x .‫ח‬
0  x   : sin 2 x  8cos2 x .‫ז‬
0  x  2 : 2sin x  5cos x
:)‫) פתור את המשוואות הבאות בתחום המצוין לידן (שימוש בזהויות ממעגל היחידה‬8
0  x   : cos 2x   cos3x .‫ב‬
0  x   : sin x   sin 3x .‫א‬


0  x   : sin  x     cos x
6



0  x   : sin  2 x    cos   x  .‫ד‬
4

0  x  2 : sin   x   cos  0.3  2 x  .‫ו‬
.‫ג‬
0  x   : sin 3x   cos   x  .‫ה‬
:)‫) פתור את המשוואות הבאות בתחום המצוין לידן (שימוש בזהויות של זווית כפולה‬9
2 sin x  sin 2 x  0 .‫ב‬
0  x  2 : sin x  sin 2x  0 .‫א‬
0  x   : 2cos 2x  sin 4 x  0 .‫ד‬
0  x  2 : 4cos x  sin 2 x .‫ג‬
0  x  2 :
0  x   : cos 2 x  2sin x
.‫ו‬
0  x  2 : 3cos x  cos 2 x  0 .‫ה‬
0  x  2 : 2sin 2 x  cos 2 x  2 .‫ח‬
0  x  2 : sin x  cos 2x  1 .‫ז‬
0  x   : 4cos 2 x  6sin x  5
.‫י‬
  x  2 : cos 2 x  4sin 2 x-sin x .‫ט‬
127
0  x  2 : cos 4 x  1  3sin 2 x .‫יא‬
0  x   : cos 4 x  sin 2 x  1 .‫יב‬
11
5 4
 3
 5
 .‫ ד‬x   ,  .‫ ג‬x  ,  .‫ ב‬x  ,  .‫) א‬1
3
6
3 3
4 4
6 6
3
 7
5
. x  0.7 .‫ י‬x  0.753 ,0.246 .‫ ט‬x 
.‫ ח‬x  ,  .‫ ז‬x    .‫ו‬
4
6 6
6
.‫ אין פתרון‬.‫ יב‬x  1.437 ,0.437 .‫יא‬
.x  

7
6
.‫ ה‬x   ,
5
23
 5 13
 ,  .‫ ב‬x  ,  ,  .‫) א‬2
12 36
18 18 18
. x  0.036 ,0.28 .‫ ו‬x  0.13 ,0.53 .‫ ה‬x  0.11 ,0.38 .‫ד‬
. x  0.15 ,0.25 .‫ ג‬x 
x   .‫ ו‬x  0, 2 .‫ ה‬x 
 5
.x  ,
6 18
,
 3
3

,  .‫ ד‬x   .‫ ג‬x 
.‫ ב‬x  0,  , 2 .‫) א‬3
2 2
2
2
 5
. x  ,  .‫ ח‬x  0,  , 2 .‫ז‬
4 4
17
 2 13 8
7
3
 .‫ ד‬x  0.0135 .‫ ג‬x  ,  ,  ,  .‫ ב‬x   ,  .‫) א‬4
18
18 9 18 9
12 4

 10
 4
 4
. x  0, .‫ ח‬x  ,  .‫ ז‬x  ,  .‫ ו‬x  ,  .‫ה‬
4
9 9
9 9
3 3
. x  0,0.5 ,  .‫ י‬x  0,0.5 ,  ,1.5 , 2 .‫ט‬
5

2
 

 5
 , , 0.05 .‫ ה‬x  0,  ,  .‫ ד‬x  , .‫ ג‬x  .‫ ב‬x  ,  .‫) א‬5
12 12
3
6 3
6
6 6
7 11 
5 
. x  0.5 ,1.23 ,1.76 .‫ ח‬x   ,  , .‫ ז‬x   , .‫ו‬
6
6
2
6 2
3 7
 5
. x  0.08 ,0.416 .‫ יב‬x   ,  .‫ יא‬x  2 ,0 .‫ י‬x  ,  ,1.1 ,1.89 .‫ט‬
4 4
6 6
.x 
x
 3
 5 3
 5
 5
 5
,  .‫ ה‬x  ,  ,  .‫ ד‬x  ,  .‫ ג‬x  ,  .‫ ב‬x  ,  .‫) א‬6
4 4
6 6 2
3 3
6 6
3 3
 9
5 
 2
. x  ,  .‫ ט‬x  0,  , 2 .‫ ח‬x   , , 0,  , 2 .‫ ז‬x  ,  .‫ו‬
8 8
3 3
3 3
5
5 17
. x  0.1 ,0.2 .‫ יב‬x  1.1 ,0.1 .‫ יא‬x   ,  ,  .‫י‬
18 6 18
128
3 7
 5
x  0.1 ,1.1 .‫ ד‬x  0.35 ,1.35 .‫ ג‬x   ,  .‫ ב‬x  ,  .‫) א‬7
4 4
4 4
x
 5
,  .‫ ח‬x  0.608 ,0.39 .‫ ז‬x  1.62 ,0.62 .‫ ו‬x  0.33 ,1.33 .‫ה‬
6 6
.x 
x
 3
,
4 4
5
2
 2

3
 .‫ ד‬x   .‫ ג‬x  ,  ,  .‫ ב‬x  0,, ,  ,  , 2 .‫) א‬8
12
3
5 5
2
2
4 14 8 9
5  
. x   ,  ,  ,  .‫ ו‬x   , , .‫ה‬
15 15 5 5
8 8 4
 3
3
4
5
4
5
3

.‫ ד‬x  ,  .‫ ג‬x   ,  , 0,  , 2 .‫ ב‬x   , , 0,  , 2 .‫) א‬9
2 2
3
 5
x  ,  , 0,  , 2 .‫ ז‬x  0.12 ,0.88 .‫ ו‬x  0.59 ,1.41 .‫ה‬
6 6
 5
 2 4 5
x  ,  , 0.08 , 0.91 .‫ י‬x  1.89 ,1.1 .‫ ט‬x  ,  ,  ,  .‫ח‬
6 6
3 3 3 3
 5 13 17
. x  0,0.38 ,0.615 ,  .‫ יב‬x  ,  ,  ,  .‫יא‬
12 12 12 12
129
‫טריגונומטריה במישור‪:‬‬
‫משפט הסינוסים‪:‬‬
‫במשולש‪ ,‬צלע חלקי סינוס הזווית שמולה הוא גודל קבוע‬
‫והוא שווה לפעמיים רדיוס המעגל החוסם‪.‬‬
‫‪a‬‬
‫‪b‬‬
‫‪c‬‬
‫‪‬‬
‫‪‬‬
‫בצורה מתמטית‪ 2 R :‬‬
‫‪sin  sin  sin ‬‬
‫‪.‬‬
‫משפט הקוסינוסים‪:‬‬
‫‪c2  a 2  b2  2ab cos ‬‬
‫או‬
‫‪a 2  b2  c 2‬‬
‫‪2ab‬‬
‫‪. cos  ‬‬
‫מתי נשתמש בכל משפט‪:‬‬
‫‪ ‬נשתמש במשפט הסינוסים כאשר‪:‬‬
‫א‪ .‬נתונות שתי זוויות וצלע‪.‬‬
‫ב‪ .‬נתונות שתי צלעות והזווית מול אחת מהן‪.‬‬
‫ג‪ .‬נתון רדיוס המעגל החוסם וצלע‪/‬זווית נוספת‪.‬‬
‫‪ ‬נשתמש במשפט הקוסינוסים כאשר‪:‬‬
‫א‪ .‬נתונות שתי צלעות והזווית ביניהן‪.‬‬
‫ב‪ .‬נתונות שלוש צלעות‪.‬‬
‫‪ ‬כאשר ישנם יותר נתונים מאשר בסעיפים שלהלן ייתכן שנוכל להשתמש בשני‬
‫המשפטים‪ .‬בבחירת המשפט שבו נשתמש כדאי לזכור שבמשפט הסינוסים‬
‫ייתכנושתי תשובות לזווית‪ ,‬גם אם בפועל רק אחת נכונה‪ ,‬ובמשפט הקוסינוסים‬
‫תתקבל בוודאות הזווית הנכונה‪.‬‬
‫שטחים של משולשים ומרובעים‪:‬‬
‫‪a  h ab sin  a sin  sin ‬‬
‫‪‬‬
‫‪‬‬
‫שטח משולש ניתן לחישוב ע"י‪:‬‬
‫‪2‬‬
‫‪2‬‬
‫‪2sin ‬‬
‫‪k k sin ‬‬
‫‪.S  1 2‬‬
‫שטח מרובע ניתן לחישוב ע"י אלכסוניו‪:‬‬
‫‪2‬‬
‫‪2‬‬
‫‪130‬‬
‫‪. S ‬‬
131
‫‪ )1‬מצא את ערכו של ‪  / x / y‬במשולשים הבאים‬
‫(‪ R‬הוא רדיוס המעגל החוסם‪ ,‬נתוני הצלעות בס"מ)‪:‬‬
‫ב‪.‬‬
‫א‪.‬‬
‫‪1150‬‬
‫‪420‬‬
‫‪560‬‬
‫ד‪.‬‬
‫ג‪.‬‬
‫‪220‬‬
‫ה‪.‬‬
‫‪600‬‬
‫‪ )2‬מצא את ערכו של ‪  / x‬במשולשים הבאים‪:‬‬
‫א‪.‬‬
‫ד‪.‬‬
‫ג‪.‬‬
‫ב‪.‬‬
‫‪530‬‬
‫‪ )3‬נתון משולש שווה שוקיים ‪ ) AB  AC ( ABC‬שאורך השוק שלו הוא ס"מ וגודלה‬
‫של זווית הבסיס בו הוא ‪ CD . 70o‬הוא חוצה זווית הבסיס ‪. C‬‬
‫מצא את אורכו של הקטע ‪. AD‬‬
‫‪132‬‬
133
‫‪ )4‬אלכסוני המלבן ‪ ABCD‬נפגשים בנקודה ‪. M‬‬
‫הנקודה ‪ G‬נמצאת על המשך הצלע ‪. AD‬‬
‫נתון‪. DG  1.2cm , AB  4cm , AD  3cm :‬‬
‫מצא את גודלו של הקטע ‪. GM‬‬
‫‪ )5‬מרובע שאורכי אלכסוניו ‪ 8‬ס"מ ו‪ 11-‬ס"מ חסום במעגל שאורך רדיוסו הוא ‪ 6‬ס"מ‪.‬‬
‫חשב את זוויות המרובע‪.‬‬
‫‪A‬‬
‫‪ )6‬הצלע ‪ AB‬במשולש ‪ ABC‬היא מיתר במעגל שמרכזו ‪. O‬‬
‫הצלע ‪ AC‬עוברת במרכז המעגל כמתואר בשרטוט‪.‬‬
‫נתון‪. BAC  38o , OC  3cm , BC  9cm :‬‬
‫מצא את אורכם של רדיוס המעגל ושל הצלע ‪. AB‬‬
‫‪O‬‬
‫‪B‬‬
‫‪C‬‬
‫‪ )7‬אחד האלכסונים במקבילית יוצר זווית של ‪ 30o‬עם צלע אחת של המקבילית‬
‫וזווית של ‪ 61.05‬עם הצלע הסמוכה לה‪ .‬אחת מצלעות המקבילית גדולה ב‪3-‬‬
‫ס"מ מהצלע הסמוכה לה‪ .‬חשב את היקף המקבילית‪.‬‬
‫‪ )8‬המשולש ‪ ABD‬חסום במעגל שרדיוסו ‪ . R‬המשך‬
‫הצלע ‪ AD‬והמשיק למעגל בנקודה ‪ B‬נפגשים בנקודה ‪.C‬‬
‫נתון‪. ADB   , C   :‬‬
‫הבע באמצעות ‪  , R‬ו ‪  -‬את אורך הקטע ‪. BC‬‬
‫‪D‬‬
‫‪C‬‬
‫‪B‬‬
‫‪ BE )9‬ו‪ CF-‬הם תיכונים במשולש ‪ ABC‬הנפגשים בנקודה ‪.M‬‬
‫מהנקודה ‪ F‬מעבירים קטע ‪ GD‬כך שמתקיים‪ AC  DC :‬ו‪. GD BE -‬‬
‫א‪.‬‬
‫‪AG 3‬‬
‫הוכח‪ :‬‬
‫‪BD 4‬‬
‫‪.‬‬
‫ב‪ .‬נתון כי‪ 4 :‬ס"מ ‪ . ME ‬חשב את אורך הקטע ‪.DG‬‬
‫ג‪ .‬נתון כי‪. ACD  48.189 :‬‬
‫הוכח כי המשולש ‪ DGC‬הוא שווה שוקיים‪.‬‬
‫‪ )11‬נתון משולש ‪ .ABC‬הקודקודים ‪ B‬ו‪ C-‬של המשולש ‪ ABC‬נמצאים‬
‫על מעגל שמרכזו ‪ .O‬מרכז המעגל ‪ O‬מונח על הצלע ‪.AC‬‬
‫אורך הצלע ‪ AB‬הוא ‪ 12‬ס"מ ואורך הקטע ‪ AO‬הוא ‪ 4.5‬ס"מ‪.‬‬
‫זווית ‪ BAC‬היא ‪. 60‬‬
‫א‪ .‬חשב את רדיוס המעגל‪.‬‬
‫ב‪ .‬מעבירים את הקוטר ‪ BD‬ואת הקטע ‪ AD‬כך‬
‫שנוצר המשולש ‪ .ADB‬חשב את זווית ‪.ADB‬‬
‫‪134‬‬
‫‪A‬‬
‫‪ )11‬המשולש ‪ ABC‬הוא שווה שוקיים ‪  AB  AC ‬החסום במעגל‬
‫שרדיוסו ‪ . R‬הנקודה ‪ E‬היא אמצע הבסיס ‪ BC‬והנקודה ‪D‬‬
‫היא אמצע הקשת ‪. AB‬‬
‫ידוע כי זווית הבסיס של המשולש היא ‪. 80‬‬
‫א‪ .‬הבע באמצעות ‪ R‬את הקטעים ‪ CD‬ו‪.DE-‬‬
‫ב‪ r .‬הוא רדיוס המעגל החוסם את המשולש ‪.CED‬‬
‫הבע באמצעות ‪ R‬את ‪. r‬‬
‫‪ AC ,AB )12‬ו ‪ AD-‬הם מיתרים במעגל המקיימים‪. BC  BD :‬‬
‫מהנקודה ‪ E‬שעל המעגל מעבירים את המיתרים ‪ AE‬ו ‪.BE-‬‬
‫המיתרים ‪ BE‬ו‪ AD-‬נחתכים בנקודה ‪.F‬‬
‫נתון כי‪. AC  AF  EF :‬‬
‫א‪ .‬הוכח‪. ABF  ABC :‬‬
‫ב‪ .‬נתון גם‪. 3  CAB  DAE :‬‬
‫הוכח כי המשולש ‪ AFE‬הוא שווה צלעות‪.‬‬
‫‪ )13‬המרובע ‪ ABCD‬הוא טרפז שווה שוקיים ‪.  AB CD , AD  BC‬‬
‫מידות הטרפז הן‪ 12 :‬ס"מ ‪ 8 , CD ‬ס"מ ‪ 6 , BC ‬ס"מ ‪. AB ‬‬
‫א‪ .‬מצא את זווית ‪( C‬עגל למספר שלם)‪.‬‬
‫ב‪ .‬מצא את אורך אלכסון הטרפז‪.‬‬
‫ג‪ .‬חשב את רדיוס המעגל החוסם את הטרפז‪.‬‬
‫‪ )14‬המרובע ‪ ABCD‬הוא טרפז ישר זווית ‪.  AB CD , B  90‬‬
‫מסמנים את הבסיס‪ AB  t :‬וידוע כי‪. AD  3t , DC  1.6t :‬‬
‫היקף הטרפז הוא‪ 40 :‬ס"מ‪.‬‬
‫א‪ .‬הבע באמצעות ‪ t‬את אורך האלכסון ‪.AC‬‬
‫ב‪ .‬ידוע גם כי‪. D  60 :‬‬
‫‪ .1‬חשב את אורך הקטע ‪.AC‬‬
‫‪ .2‬חשב את שטח הטרפז‪.‬‬
‫‪135‬‬
‫‪ )15‬המשולש ‪ ABC‬הוא שווה שוקיים ‪  AB  AC ‬בעל זווית ראש ‪ 36‬החסום‬
‫במעגל שקוטרו ‪ 16‬ס"מ‪ .‬מעבירים תיכון לשוק ‪.BD‬‬
‫א‪ .‬מצא את אורך הבסיס ‪ BC‬במשולש‪.‬‬
‫ב‪ .‬חשב את אורך התיכון ‪.BD‬‬
‫ג‪ .‬מסמנים‪:‬‬
‫‪ - r1‬רדיוס המעגל החוסם את המשולש ‪.ABD‬‬
‫‪ - r2‬רדיוס המעגל החוסם את המשולש ‪.BCD‬‬
‫‪r1‬‬
‫הוכח את היחס הבא‪ 2cos 36 :‬‬
‫‪r2‬‬
‫‪.‬‬
‫‪ )16‬המרובע ‪ ABCD‬הוא טרפז ‪.  AB CD ‬‬
‫מעבירים את האלכסון ‪ BD‬המקיים‪. BCD  ADB :‬‬
‫נתון כי‪ 20 :‬ס"מ ‪ 10 , CD ‬ס"מ ‪ 5 , AD ‬ס"מ ‪. AB ‬‬
‫כמו כן ידוע כי השוק ‪ BC‬גדולה פי ‪ 2‬מהאלכסון ‪.BD‬‬
‫א‪ .‬הראה כי השוק ‪ BC‬שווה לבסיס ‪.CD‬‬
‫ב‪ .‬חשב את זווית ‪.C‬‬
‫ג‪ .‬ממשיכים את שוקי הטרפז ‪ AD‬ו ‪ BC-‬עד לנקודה ‪ E‬שמחוץ לטרפז‪.‬‬
‫חשב את רדיוס המעגל החוסם את המשולש ‪.CDE‬‬
‫‪ )17‬באיור שלפניך נתון המרובע ‪ .ABCD‬ידוע כי‪ . D  90 :‬נסמן את הצלעות‬
‫באופן הבא‪. AB  6 x , BC  5x , CD  8x , AD  3x :‬‬
‫א‪ .‬חשב את זווית ‪.BDC‬‬
‫ב‪ E .‬היא נקודה הנמצאת על אמצע הצלע ‪.BC‬‬
‫מעבירים את הקטעים ‪ AE‬ו‪ DE-‬כך ש‪DE-‬‬
‫‪S ABE‬‬
‫מקביל ל‪ .AB-‬חשב את היחס הבא‪:‬‬
‫‪S ECD‬‬
‫‪136‬‬
‫‪.‬‬
‫‪ )18‬מהנקודה ‪ O‬מעבירים את הקטעים ‪ OC , OB , OA‬ו‪.OD-‬‬
‫ידוע כי זווית ‪ AOB‬שווה לזווית ‪ COD‬והיא מסומנת ב‪.  -‬‬
‫המשולש ‪ COD‬הוא ישר זווית ‪.  CDO  90‬‬
‫נתונים האורכים‪. AO  8 , BO  9 , DO  10 :‬‬
‫מסמנים‪. BC  1.4m , CD  1.5m :‬‬
‫א‪ .‬הבע באמצעות ‪ m‬את ‪. sin ‬‬
‫(העזר במשולש ‪ COD‬ובטא תחילה את ‪.)CO‬‬
‫ב‪ .‬נתון גם כי‪ . AB  m :‬מצא את ‪ m‬אם ידוע כי רדיוס המעגל החוסם את‬
‫‪2‬‬
‫המשולש ‪ AOB‬הוא‬
‫‪3‬‬
‫ג‪.‬‬
‫‪.8‬‬
‫חשב את זווית ‪.BOC‬‬
‫‪ )19‬במשולש ‪ ABC‬הזווית ‪ A‬היא בת ‪. 60‬‬
‫מעבירים את הקטע ‪ AD‬כך שנוצרת זווית‪. ADB  60 :‬‬
‫ידוע כי ‪ AB  28‬וכי הצלע ‪ AD‬במשולש ‪ ABD‬גדולה פי ‪ 1.5‬מהצלע ‪.BD‬‬
‫א‪ .‬מצא את אורך הצלע ‪.BD‬‬
‫ב‪ .‬היקף המשולש ‪ ABC‬הוא‪. P  5 7  7 :‬‬
‫‪ .1‬סמן‪ DC  t :‬והבע באמצעות ‪ t‬את אורך הצלע ‪.AC‬‬
‫‪ .2‬מצא את ‪. t‬‬
‫ג‪ .‬חשב את שטח המשולש ‪.ABC‬‬
‫‪ )21‬מהנקודה ‪ A‬מעבירים את הקטעים ‪ AB‬ו‪ .AC-‬הנקודה ‪D‬‬
‫היא אמצע ‪ AC‬וממנה מעבירים את ‪ DE‬המקביל ל‪.AB-‬‬
‫הנקודות ‪ E , C‬ו ‪ F-‬נמצאות על אותו הישר‪.‬‬
‫ידוע כי המשולשים ‪ DEF , ABD‬ו‪ DCE-‬הם‬
‫שווי שוקיים‪.  AB  BD , DC  CE , EF  DE  :‬‬
‫נתון כי‪. AD  8 :‬‬
‫א‪ .‬חשב את אורך הקטע ‪.BF‬‬
‫ב‪ .‬מחברים את הנקודות ‪ B‬ו‪.C -‬‬
‫חשב את אורך הצלע ‪.BC‬‬
‫‪A‬‬
‫‪ )21‬בשרטוט נתון‪. AD  5cm , AC  8cm , AB  6cm :‬‬
‫הנקודה ‪ D‬היא אמצע הצלע ‪. BC‬‬
‫‪137‬‬
‫‪C‬‬
‫‪D‬‬
‫‪B‬‬
138
‫‪ )22‬הצלע ‪ AC‬במשולש ‪ ABC‬גדולה פי ‪ 4‬מהצלע ‪. AB‬‬
‫הנקודה ‪ E‬היא אמצע הצלע ‪ AC‬והנקודה ‪ D‬נמצאת על הצלע ‪BC‬‬
‫כך שמתקיים ‪ . DC  2BD‬נתון‪. BC  b , AB  a :‬‬
‫הבע באמצעות ‪ a‬ו‪ b -‬את אורך הקטע ‪. DE‬‬
‫‪A‬‬
‫‪E‬‬
‫‪C‬‬
‫‪B‬‬
‫‪D‬‬
‫‪ )23‬המשולש ‪ ABD‬חסום במעגל שרדיוסו ‪. R‬‬
‫המשך הצלע ‪ AD‬והמשיק למעגל בנקודה ‪ B‬נפגשים בנקודה ‪.C‬‬
‫נתון‪. ADB   , C   :‬‬
‫הבע באמצעות ‪  , R‬ו ‪  -‬את אורך הקטע ‪. BC‬‬
‫‪A‬‬
‫‪D‬‬
‫‪C‬‬
‫‪B‬‬
‫‪ AC )24‬ו‪ BD -‬הם מיתרים במעגל שרדיוסו ‪ , R‬שנפגשים בנקודה ‪. M‬‬
‫זווית ‪ B‬היא זווית ישרה‪.‬‬
‫נתון‪. DC  q , DM  p , AB  k :‬‬
‫הבע באמצעות ‪ p , k , R‬ו‪ q -‬את אורך הקטע ‪. MC‬‬
‫‪A‬‬
‫‪D‬‬
‫‪M‬‬
‫‪C‬‬
‫‪ )25‬חשב את שטחי המשולשים הבאים‪:‬‬
‫‪240‬‬
‫‪320‬‬
‫‪480‬‬
‫‪ )26‬חשב את שטחו של טרפז שווה שוקיים שאורך האלכסון שלו ‪ 8‬ס"מ והוא יוצר‬
‫זווית של ‪ 15‬עם הבסיסים‪.‬‬
‫‪ )27‬אורכו של מלבן הוא ‪ m‬ורוחבו ‪ . n‬הזווית שבין אלכסוני המלבן היא ‪.‬‬
‫‪2mn‬‬
‫הוכח כי מתקיים‪:‬‬
‫‪m2  n 2‬‬
‫‪. sin  ‬‬
‫‪ )28‬במשולש ישר זווית ‪) B  90o ( ABC‬‬
‫נתון‪. A   , AB  m :‬‬
‫הבע באמצעות ‪ ‬ו‪ m -‬את שטח המשולש ‪. BCD‬‬
‫‪BD‬‬
‫חוצה את הזווית‬
‫‪B‬‬
‫‪ )29‬באיור שלפניך נתון משושה משוכלל ששטחו הכולל הוא‪. S :‬‬
‫א‪ .‬הבע באמצעות ‪ S‬את אורך צלע המשושה‪.‬‬
‫ב‪ .‬מעבירים אלכסונים במשושה כך שנוצר המלבן ‪.BFEC‬‬
‫ג‪ .‬הבע באמצעות ‪ S‬את שטח המלבן‪.‬‬
‫‪139‬‬
‫‪.‬‬
‫‪B‬‬
‫‪ )31‬המשולש ‪ ABC‬הוא שווה שוקיים בעל זווית ראש ‪.  AB  AC , ‬‬
‫אורך הבסיס ‪ BC‬הוא ‪ . k‬על השוק ‪ AB‬בונים משולש ישר זווית ‪ABD‬‬
‫ובו ‪. D  90‬‬
‫א‪ .‬הבע באמצעות ‪ k‬ו‪  -‬את אורך שוק המשולש ‪.ABC‬‬
‫ב‪ .‬הניצב ‪ AD‬במשולש ‪ ABD‬שווה ל‪ 0.85k -‬וכי‪. ABD  40 :‬‬
‫מצא את זוויות המשולש ‪.ABC‬‬
‫ג‪ .‬חשב את שטח המרובע ‪ ABCD‬אם ידוע כי ‪. k  6‬‬
‫‪ )31‬במשולש ‪ ABC‬אורך הצלע ‪ AC‬הוא ‪ 8‬ס"מ ואורך הצלע ‪ AB‬הוא ‪ 10‬ס"מ‪.‬‬
‫הנקודה ‪ E‬היא אמצע הצלע ‪ AC‬והנקודה ‪ D‬מקיימת‪ :‬ס"מ ‪. AD  3‬‬
‫‪DE 2‬‬
‫ידוע כי‪ :‬‬
‫‪BC 5‬‬
‫‪.‬‬
‫א‪ .‬מצא את אורך הקטע ‪.DE‬‬
‫ב‪ .‬חשב את רדיוס המעגל החוסם את המשולש ‪.ADE‬‬
‫ג‪ .‬חשב את שטח המרובע ‪.BCED‬‬
‫הקטע ‪ AC‬הוא אלכסון בטרפז‪.‬‬
‫מסמנים‪. AC  m , ACD   , ADC   :‬‬
‫א‪ .‬הבע באמצעות ‪  , ‬ו‪ m -‬את אורך הבסיס הגדול ‪.DC‬‬
‫ב‪.‬‬
‫‪SADC‬‬
‫נתון כי האלכסון ‪ AC‬מקיים‪ 3 :‬‬
‫‪SABC‬‬
‫ג‪.‬‬
‫חשב את שטח הטרפז אם ידוע כי‪   40 ,   60 :‬ו‪. m  8 -‬‬
‫‪ .‬הבע באמצעות ‪  , ‬ו‪ m -‬את הבסיס ‪.AB‬‬
‫‪ )33‬המרובע ‪ ABCD‬הוא מלבן‪ .‬מעבירים את האלכסון ‪BD‬‬
‫וממשיכים אותו עד לנקודה ‪ E‬שמחוץ למלבן‪.‬‬
‫מחברים את הנקודה ‪ E‬עם הקודקוד ‪.C‬‬
‫ידוע כי אורך הצלע ‪ AD‬של המלבן הוא ‪ 6‬ס"מ‬
‫וכי אורך הקטע ‪ BE‬הוא ‪ 9‬ס"מ‪ .‬הזווית ‪ CBE‬היא ‪.115‬‬
‫א‪ .‬מצא את אורך הקטע ‪.CE‬‬
‫ב‪ .‬מצא את אורך האלכסון ‪.BD‬‬
‫ג‪ .‬חשב את שטח המשולש ‪.DCE‬‬
‫‪140‬‬
‫ממשיכים את השוקיים ‪ AD‬ו ‪ BC-‬עד לפגישתם בנקודה ‪.E‬‬
‫ידוע כי‪. DE  CE :‬‬
‫מעבירים את האלכסון ‪ AC‬אשר חוצה את זווית ‪.C‬‬
‫מסמנים את הבסיס הגדול ‪ DC‬ב ‪ k -‬ואת‪. ACD   :‬‬
‫א‪ .‬הבע באמצעות ‪ k‬ו‪  -‬את הבסיס הקטן של הטרפז ‪.AB‬‬
‫ב‪ .‬הבע באמצעות ‪ k‬ו‪  -‬את שטח המשולש ‪.ABC‬‬
‫ג‪ .‬חשב את שטח המשולש ‪ ABC‬כאשר‪ 12 ,   15 :‬ס"מ ‪. k ‬‬
‫‪ )35‬נתונה מקבילית ‪ ABCD‬ובה מעבירים את האלכסונים ‪ AC‬ו‪ BD-‬אשר נחתכים‬
‫בנקודה ‪ M‬כמתואר באיור‪.‬‬
‫מסמנים‪. AB  k , BDC   , ACD   :‬‬
‫א‪.‬‬
‫‪AC sin ‬‬
‫‪‬‬
‫הוכח כי אלכסוני המקבילית מקיימים‪:‬‬
‫‪BD sin ‬‬
‫‪.‬‬
‫ב‪ .1 .‬הבע באמצעות ‪  , ‬ו‪ k -‬את שטח המשולש ‪.DMC‬‬
‫‪ .2‬הבע באמצעות ‪  , ‬ו‪ k -‬את שטח המקבילית ‪.ABCD‬‬
‫ג‪.‬‬
‫‪AC‬‬
‫‪4k 2 sin 2 ‬‬
‫נתון כי‪ 2 :‬‬
‫‪ .‬הראה כי שטח המקבילית הוא‪:‬‬
‫‪BD‬‬
‫‪sin    ‬‬
‫‪ )36‬המרובע ‪ ABCD‬הוא מעוין ובו ‪ . D  60‬מעבירים את‬
‫האלכסון ‪ AC‬ואת הקטע ‪ CE‬כך שהנקודה ‪ E‬נמצאת על‬
‫‪BE‬‬
‫הצלע ‪ AB‬ומחלקת אותה ביחס‪ 4 :‬‬
‫‪AE‬‬
‫‪.‬‬
‫א‪ .‬חשב את זווית ‪.AEC‬‬
‫ב‪ .‬נתון כי שטח המשולש ‪ AEC‬הוא ‪ 8.66‬סמ"ר‪.‬‬
‫חשב את שטח המעוין‪.‬‬
‫‪ )37‬הקטע ‪ DE‬מקביל לצלע ‪ BC‬במשולש ‪ ABC‬כמתואר באיור‪.‬‬
‫נתון כי‪. BD  129 , BC  15 , CE  13 :‬‬
‫ידוע כי זווית ‪ AED‬היא ‪. 60‬‬
‫א‪ .‬חשב את אורך הקטע ‪ DE‬אם ידוע כי הוא קטן מ‪ 10-‬ס"מ‪.‬‬
‫ב‪ .‬חשב את שטח המשולש ‪.ADE‬‬
‫‪141‬‬
‫‪.‬‬
‫‪ )38‬המשולש ‪ ABC‬חסום במעגל כך ש ‪ AB-‬הוא קוטר‪.‬‬
‫הנקודה ‪ D‬היא אמצע הקשת ‪ BC‬וממנה מעבירים את‬
‫המיתרים ‪ AD‬ו ‪ BD-‬ומעלים גובה ‪ DE‬לצלע ‪. BC‬‬
‫מסמנים‪ DE  k :‬ונתון כי‪. ABC  10 :‬‬
‫א‪ .‬הבע באמצעות ‪ k‬את רדיוס המעגל‪.‬‬
‫ב‪ .‬הבע באמצעות ‪ k‬את שטח המשולש ‪.ABF‬‬
‫ג‪ .‬מצא את ‪ k‬אם ידוע כי שטח המשולש ‪ ABF‬הוא ‪ 15.363‬סמ"ר‪.‬‬
‫‪ )39‬במשולש ‪ ABC‬הקטע ‪ BE‬חוצה את זווית ‪.B‬‬
‫הנקודה ‪ D‬היא אמצע הצלע ‪ AB‬ומקיימת‪. DE  CE :‬‬
‫ידוע כי‪. BC  6 , BE  8 , BD  9 :‬‬
‫א‪ .‬מצא את זווית ‪.B‬‬
‫ב‪ .‬חשב את שטח המשולש ‪.ADE‬‬
‫‪ )41‬נתון המעוין ‪.ABCD‬אורך האלכסון הגדול במעוין ‪ AC‬גדול פי ‪ 1.8‬מצלע המעוין‪.‬‬
‫א‪ .‬חשב את זוויות המעוין‪.‬‬
‫מהקודקוד ‪ D‬מעבירים את הקטע ‪ DE‬שאורכו הוא ‪. m‬‬
‫הקטע ‪ DE‬חותך את האלכסון ‪ AC‬בנקודה ‪.G‬‬
‫הזווית ‪ EDC‬תסומן ב ‪. -‬‬
‫ב‪ .‬הבע באמצעות ‪ m‬ו‪  -‬את אורך הקטע ‪.CE‬‬
‫ג‪ .‬הבע באמצעות ‪ m‬ו‪  -‬את שטח המשולש ‪.EGC‬‬
‫‪ )41‬המשולש ‪ ABC‬חסום במעגל כמתואר באיור‪.‬‬
‫מעבירים את המיתר ‪ AD‬החוצה את זווית ‪.BAC‬‬
‫ידוע כי‪ . BAC  40 , ACB  60 :‬מסמנים‪. AD  k :‬‬
‫א‪ .‬הבע באמצעות ‪ k‬את אורך המיתר ‪.BD‬‬
‫ב‪ .‬ידוע כי שטח המשולש ‪ ABD‬הוא ‪ 7.368‬סמ"ר‪.‬‬
‫מצא את ‪( k‬עגל למספר שלם)‪.‬‬
‫‪ )42‬המשולש ‪ ABC‬הוא שווה שוקיים ‪ .  AB  AC ‬ממשיכים את‬
‫הצלע ‪ AC‬עד לנקודה ‪ D‬כך שאורך שוק המשולש גדולה פי ‪3.8‬‬
‫מהקטע ‪ .AD‬ידוע כי‪ . D  60 :‬אורך הקטע ‪ BD‬הוא ‪ 21‬ס"מ‪.‬‬
‫א‪ .‬מצא את אורך הקטע ‪.AD‬‬
‫ב‪ .‬חשב את שטח המשולש ‪.ABC‬‬
‫‪142‬‬
‫‪ )43‬במקבילית ‪ ABCD‬אורך האלכסון ‪ AC‬הוא ‪ 79‬ס"מ‪.‬‬
‫היקף המקבילית הוא ‪ 20‬ס"מ וידוע כי‪. B  120 :‬‬
‫א‪ .‬מצא את אורכי צלעות המקבילית‪.‬‬
‫ב‪ .‬חשב את שטח המקבילית‪.‬‬
‫ג‪ .‬מסמנים נקודה ‪ E‬על האלכסון ‪ AC‬כך‬
‫שהמרובע ‪ CBED‬הוא בר חסימה‪.‬‬
‫חשב את רדיוס המעגל החוסם את המרובע ‪.CBED‬‬
‫‪ )44‬המרובע ‪ ABCD‬הוא מלבן החסום במעגל‪ .‬מהקדקוד ‪ D‬מעבירים‬
‫את המיתר ‪ DF‬החותך את הצלע ‪ AB‬בנקודה ‪.E‬‬
‫ידוע כי‪ . AF  CF :‬הצלע ‪ AD‬של המלבן תסומן ב‪. a -‬‬
‫א‪ .‬הוכח כי המשולש ‪ DAE‬הוא שווה שוקיים‪.‬‬
‫ב‪ .‬נתון גם כי‪. BC  BF :‬‬
‫‪ .1‬הבע באמצעות ‪ a‬את רדיוס המעגל‪.‬‬
‫‪ .2‬חשב את הזוויות המרכזיות של הקשתות‪AB ; BC :‬‬
‫(אין צורך לסרטט אותן)‪.‬‬
‫‪ )45‬המרובע ‪ ABCD‬חסום במעגל כמתואר באיור‪.‬‬
‫ידוע כי‪. AB  b , BC  a , CD  a , AD  3b :‬‬
‫א‪ .‬הבע באמצעות ‪ a‬ו‪ b -‬את ‪. cos BCD‬‬
‫ב‪ .‬הוכח כי אם ‪ BD‬קוטר אז מתקיים‪. a  b 5 :‬‬
‫ג‪ .‬נתון כי רדיוס המעגל הוא ‪ 3‬ס"מ‪.‬‬
‫הסתמך על סעיף ב' וחשב את שטח המרובע ‪.ABCD‬‬
‫‪ )46‬המשולש ‪ ABC‬הוא ישר זווית ‪  C  90‬ובו‪. B  2 :‬‬
‫מעבירים מעגל שרדיוסו ‪ R‬דרך הקדקודים ‪ B‬ו‪ C-‬אשר חותך‬
‫את צלעות המשולש בנקודות ‪ D‬ו‪.E-‬‬
‫המיתר ‪ BE‬חוצה את זווית ‪.B‬‬
‫א‪ .‬הבע באמצעות ‪ R‬ו‪  -‬את שטח המשולש ‪.ABE‬‬
‫ב‪ .‬ידוע כי המשולש ‪ ABE‬הוא שווה שוקיים וכי אורך‬
‫המיתר ‪ CE‬הוא ‪ 6‬ס"מ‪ .‬חשב את שטח המשולש ‪.ABE‬‬
‫‪143‬‬
‫‪ )47‬במשולש שווה שוקיים ‪ ) AB  AC ( ABC‬שאורך השוק בו הוא ‪ k‬וזווית הבסיס‬
‫שלו היא ‪ BE , ‬חוצה את זווית ‪ B‬ו‪ CD -‬הוא הגובה לשוק ‪. AB‬‬
‫הוכח כי שטח המשולש ‪ ADE‬הוא‪:‬‬
‫‪sin 4‬‬
‫‪‬‬
‫‪2‬‬
‫‪k 2 sin‬‬
‫‪3‬‬
‫‪4sin‬‬
‫‪2‬‬
‫‪. SADE  ‬‬
‫‪ )48‬נתון משולש שווה שוקיים ‪  AB  AC  ABC‬החסום במעגל‪.‬‬
‫מהקדקוד ‪ C‬מעבירים את המיתר ‪ CE‬החותך את השוק ‪AB‬‬
‫בנקודה ‪ .D‬ידוע כי ‪ E‬היא אמצע הקשת ‪ AB‬והיחס בין‬
‫הקטעים ‪ BD‬ו‪ CD-‬הוא ‪ .4:7‬מסמנים‪. ACD   :‬‬
‫א‪ .‬מצא את זוויות המשולש ‪( ABC‬עגל למספרים שלמים)‪.‬‬
‫ב‪ .‬חשב את אורך המיתר ‪ BE‬אם ידוע כי רדיוס המעגל‬
‫החוסם שווה ל‪ 8-‬ס"מ‪.‬‬
‫‪ AC )49‬ו‪ BD-‬הם מיתרים במעגל שרדיוסו ‪ , R‬שנפגשים בנקודה ‪. M‬‬
‫זווית ‪ B‬היא זווית ישרה‪.‬‬
‫נתון‪. MCB   , MBC   :‬‬
‫א‪ .‬הבע באמצעות ‪  , R‬ו ‪  -‬את שטח המשולש ‪. BDC‬‬
‫‪1‬‬
‫‪2‬‬
‫ב‪ .‬נתון‪ . SBDC  R 2 ,   2 :‬חשב את ‪.‬‬
‫‪A‬‬
‫‪D‬‬
‫‪M‬‬
‫‪C‬‬
‫‪ )51‬בטרפז שווה שוקיים‪ ,‬שאורך השוק שבו הוא ‪ b‬והזווית שליד הבסיס הגדול‬
‫היא ‪ ‬נתון שהאלכסונים מאונכים זה לזה‪.‬‬
‫א‪ .‬הבע באמצעות ‪ ‬ו‪ b -‬את אורכי בסיסי הטרפז‪.‬‬
‫ב‪ .‬חשב את ‪ ‬אם ידוע שהבסיס הגדול ארוך פי ‪ 3‬מהבסיס הקטן‪.‬‬
‫‪ )51‬המיתר ‪ AB‬הוא קוטר במעגל שרדיוסו‪ R‬ו‪ AD-‬הוא מיתר‪.‬‬
‫ממשיכים את המיתר ‪ BD‬ומעבירים משיק מהנקודה ‪.A‬‬
‫המשיק והמשך המיתר נפגשים בנקודה ‪.C‬‬
‫מסמנים‪. BAD   :‬‬
‫א‪ .‬הבע באמצעות ‪ ‬ו‪ R-‬את שטח המשולש ‪.ABD‬‬
‫ב‪ .‬הבע באמצעות ‪ ‬ו‪ R-‬את שטח המשולש ‪.ACD‬‬
‫ג‪ .‬מצא את ‪ ‬אם ידוע כי שטח המשולש ‪ ABD‬קטן‬
‫פי ‪ 4‬משטח המשולש ‪.ACD‬‬
‫‪144‬‬
‫‪B‬‬
‫‪ )52‬המרובע ‪ ABCD‬הוא מקבילית‪ .‬הקטע ‪ AE‬מקצה על‬
‫הצלע ‪ DC‬קטעים המקיימים‪. 3CE  DE :‬‬
‫מעבירים תיכון ‪ DF‬לצלע ‪ AE‬במשולש ‪.ADE‬‬
‫ידוע כי‪ . ADF  CDF   :‬מסמנים‪. CE  k :‬‬
‫א‪ .‬הבע באמצעות ‪ k‬ו‪  -‬את אורך הקטע ‪.AE‬‬
‫ב‪ .‬מעבירים את האלכסון ‪.AC‬‬
‫הבע באמצעות ‪ k‬ו‪  -‬את היקף המשולש ‪.ACE‬‬
‫ג‪ .‬היקף המשולש ‪ ACE‬הוא ‪ . 4.5k‬מצא את ‪. ‬‬
‫*הערה‪ :‬השאלות הבאות משלבות ידע בגיאומטריה ובטריגונומטריה יחד‪:‬‬
‫‪ )53‬המרובע ‪ ABCD‬הוא מלבן‪ .‬מעבירים את האלכסונים ‪ AC‬ו ‪.BD-‬‬
‫הנקודה ‪ E‬נמצאת על הצלע ‪ AB‬של המלבן ומחלקת אותה‬
‫כך ש ‪ . 2BE  AE -‬ידוע כי הקטע ‪ OE‬מאונך לאלכסון ‪AC‬‬
‫ושווה ל‪ .BE-‬הקטע ‪ CE‬חותך את האלכסון ‪ BD‬בנקודה ‪.G‬‬
‫א‪ .‬הוכח כי הקטע ‪ CE‬מאונך לאלכסון ‪.BD‬‬
‫ב‪ .‬הוכח כי מתקיים‪. 4GE  AE :‬‬
‫ג‪ .‬נתון כי שטח המשולש ‪ BEG‬הוא ‪ 5‬סמ"ר‪.‬‬
‫חשב את שטח המלבן ‪.ABCD‬‬
‫‪ )54‬באיור שלפניך נתון מחומש משוכלל ‪ACBDE‬‬
‫(כל זוויותיו הן ‪ )108‬בעל אורך צלע ‪. a‬‬
‫א‪ .‬הבע באמצעות ‪ a‬את אלכסון המחומש ‪.AD‬‬
‫ב‪ .‬הבע באמצעות ‪ a‬את רדיוס המעגל החוסם את המחומש‪.‬‬
‫ג‪ .‬הבע באמצעות ‪ a‬את שטח המחומש‪.‬‬
‫ד‪ .‬אורך רדיוס המעגל החוסם את המחומש הוא ‪ 6‬ס"מ‪.‬‬
‫חשב את שטח המחומש‪.‬‬
‫‪ )55‬במשולש ‪ ABC‬הזווית ‪ C‬היא‪. 60 :‬מעבירים את הקטע ‪ AD‬כך שנוצרים‬
‫המשולשים ‪ ACD‬ו‪.ABD-‬‬
‫ידוע כי רדיוס המעגל החוסם את המשולש ‪ ACD‬הוא‪ 3 :‬ס"מ ‪. R1 ‬‬
‫כמו כן רדיוס המעגל החוסם את המשולש ‪ ABD‬הוא‪ 3 :‬ס"מ ‪. R2 ‬‬
‫א‪ .‬הוכח כי המשולש ‪ ABC‬הוא ישר זווית‪.‬‬
‫ב‪ .‬היקף המשולש ‪ ABC‬הוא‪12  4 3 :‬ס"מ ‪. P ‬‬
‫חשב את שטח המשולש‪.‬‬
‫‪145‬‬
‫‪ )56‬המשולש ‪ ABC‬הוא שווה צלעות‪ .‬הקטע ‪ DE‬עובר דרך הקדקוד ‪ A‬כך שנוצרים‬
‫שני משולשים ‪ ABD‬ו ‪ .ACE-‬ידוע כי ‪ AC‬חוצה‬
‫את זווית ‪ DCE‬במשולש ‪.DCE‬‬
‫א‪ .‬הוכח‪. AB CE :‬‬
‫ב‪ .‬הוכח‪. BC  DE  DC  AE :‬‬
‫ג‪ .‬נתון‪ 8 :‬ס"מ ‪ DC ‬וכי‪. AC  DE :‬‬
‫‪ .1‬חשב את שטח המשולש ‪.DCE‬‬
‫‪ .2‬חשב את שטח המשולש ‪.ABD‬‬
‫‪ )57‬מהנקודה ‪ A‬מעבירים את הקטעים ‪ AD , AC , AB‬ו‪ AE-‬כך‬
‫שמתקיים‪ BAC  CAD   :‬ו ‪. AB  AE -‬‬
‫מעבירים את האלכסון ‪ BE‬במחומש ‪.ABCDE‬‬
‫מתקיים‪ . BE CD :‬ידוע כי המרובע ‪ BCDE‬הוא בר חסימה‪.‬‬
‫א‪ .‬הוכח כי המרובע ‪ BCDE‬הוא טרפז שווה שוקיים‪.‬‬
‫ב‪ .‬נתון כי המשולש ‪ ACD‬הוא ש"ש ( ‪.) AC  AD‬‬
‫הוכח כי‪. ABD  ACE :‬‬
‫ג‪ .‬ידוע כי‪ ADC  3  2.5 :‬ו‪. ADE  3 10 -‬‬
‫הוכח כי משולש ‪ ADE‬הוא ישר זווית‪.‬‬
‫ד‪ .‬נסמן‪. AB  m :‬‬
‫‪ .1‬הבע באמצעות ‪ m‬את צלעות הטרפז ‪.BCDE‬‬
‫‪ .2‬הבע באמצעות ‪ m‬את שטח המחומש ‪.ABCDE‬‬
‫‪ .3‬מצא את ‪ m‬אם ידוע כי שטח המחומש ‪ ABCDE‬הוא ‪ 46.284‬סמ"ר‪.‬‬
‫(עגל למספר שלם)‪.‬‬
‫‪ )58‬הטרפז ‪ ABCD‬הוא שווה שוקיים‪ .‬חוסמים מעגל בתוך‬
‫הטרפז אשר משיק לו בנקודות ‪ F ,E‬ו‪ G-‬כמתוארבאיור‪.‬‬
‫הקטעים ‪ DF‬ו‪ CE-‬חוצים את זוויות הטרפז ונחתכים‬
‫בנקודה ‪.M‬‬
‫א‪ .‬הוכח כי הנקודה ‪ M‬היא מרכז המעגל החסום‪.‬‬
‫ב‪ .‬חשב את זוויות הטרפז‪.‬‬
‫ג‪ .‬ממשיכים את ‪ GF‬ואת ‪ AD‬כך שהם‬
‫‪EM‬‬
‫נפגשים בנקודה ‪ .H‬חשב את היחס‬
‫‪FH‬‬
‫‪.‬‬
‫‪ )59‬המרובע ‪ BDEC‬הוא טרפז ‪.  BC DE ‬‬
‫המשכי השוקיים ‪ BD‬ו‪ CE-‬נפגשים בנקודה ‪ A‬כך‬
‫‪146‬‬
‫‪C‬‬
‫‪H‬‬
‫‪B‬‬
‫‪G‬‬
‫‪A‬‬
‫‪E‬‬
‫‪F‬‬
‫‪M‬‬
‫‪D‬‬
‫שהמשולש ‪ ABC‬הוא שווה שוקיים ‪.  AB  BC‬‬
‫נתון‪ 18 :‬ס"מ ‪. ADE  30 , AB ‬‬
‫א‪ .‬סמן את אורך הבסיס ‪ DE‬ב‪ x -‬ואת שטח‬
‫הטרפז ‪ BDEC‬ב ‪ . S -‬הבע את ‪ S‬באמצעות ‪. x‬‬
‫ב‪ .‬על הקטע ‪ AD‬בונים ריבוע‪ .‬ידוע כי שטחו קטן ב‪ 1-‬סמ"ר משטח הטרפז ‪.BDEC‬‬
‫‪S ADE‬‬
‫‪S ABC‬‬
‫‪.‬‬
‫‪ )61‬במעגל שמרכזו ‪ O‬מעבירים את הקטרים ‪ AB‬ו‪ CD-‬המאונכים זה לזה‪.‬‬
‫‪ E‬היא נקודה על היקף המעגל המקיימת‪ 15 :‬ס"מ ‪. BE  DE ‬‬
‫מעבירים את המיתר ‪ .AE‬הקטע ‪ OM‬מאונך למיתר ‪AE‬‬
‫ושווה למיתר ‪.DE‬‬
‫א‪ .‬הוכח כי המרובע ‪ OMEB‬הוא טרפז ישר זווית‪.‬‬
‫ב‪ .‬מצא את אורך המיתר ‪.BE‬‬
‫נתון כי שטח הטרפז הוא ‪ 90‬סמ"ר‪.‬‬
‫ג‪ .‬מצא את רדיוס המעגל‪.‬‬
‫ד‪ .‬חשב את זווית ‪.B‬‬
‫‪ )61‬דרך הנקודה ‪ A‬מעבירים שני משיקים למעגל ‪ AB‬ו‪.AC-‬‬
‫הנקודות ‪ D‬ו‪ E-‬נמצאות על היקף המעגל ומהן מעבירים את המיתרים ‪ DE , DC‬ו ‪.BD-‬‬
‫ממשיכים את המיתר ‪ BE‬עד לנקודה ‪ F‬שמחוץ למעגל כך ש‪ DF-‬מאונך למיתר ‪BD‬‬
‫ושווה באורכו לרדיוס המעגל‪ .‬נתון כי‪. BFD  BDC :‬‬
‫א‪ .‬הוכח כי‪. BFD  ABC :‬‬
‫ב‪ .‬הוכח כי המרובע ‪ ADFB‬הוא טרפז‪.‬‬
‫אורך המשיק ‪ AC‬הוא ‪ 8‬ס"מ ואורך‬
‫המיתר ‪ CD‬הוא ‪ 6‬ס"מ‪.‬‬
‫ג‪ .‬חשב את שטח הטרפז‪.‬‬
‫ד‪ .‬חשב את זוויות הטרפז‪.‬‬
‫‪ BD )62‬הוא אלכסון במרובע הבר‪-‬חסימה ‪ .ABCD‬הנקודות ‪ E‬ו ‪ F-‬הן בהתאמה‬
‫אמצעי הצלעות ‪ AD‬ו‪ AB-‬במרובע‪ .‬מעבירים את הקטעים ‪ BE‬ו‪CF-‬‬
‫כך ש‪ . BE CD :‬נתון כי הזוויות ‪ A‬ו‪ BFE -‬משלימות ל ‪.180 -‬‬
‫א‪ .‬הוכח‪. BCD BFE :‬‬
‫‪147‬‬
. GE  HD  17
1
:‫ וכי‬BE  7.5 :‫נתון כי‬
15
.FE ‫ חשב את אורך הקטע‬.‫ב‬
BED ‫ נתון כי רדיוס המעגל החוסם את המשולש‬.‫ג‬
. EBD ‫ מצא את זווית‬.R = ‫ ס"מ‬4.001 :‫הוא‬
  138.618 ‫ או‬  41.382 .‫ ג‬  34.231 .‫ ב‬x  18.585cm , y  22.199cm .‫) א‬1
.  73.898, x  3.606cm .‫ ה‬  24.474 ‫ או‬  155.526 .‫ד‬
. AD  13.064cm )3   90 .‫ ד‬  105.962 .‫ ג‬  20.742 .‫ ב‬x  5.646cm .‫) א‬2
. 66.444, 113.556, 41.810, 138.190 )5 GM  3.360cm )4
. R  5.395cm , AC  10.790cm )8 P  22cm )7 R  9.242cm , AB  14.56cm )6
. r  1.15R .‫ ב‬DE  1.48R CD  R 3 .‫) א‬11 24.32 .‫ ב‬.R = ‫ ס"מ‬10.5 .‫) א‬11 DG  18 .‫) ב‬9
. R  ‫ ס"מ‬6.29 .‫ ס"מ ג‬11.66 .‫ ב‬68 .‫) א‬13
.‫ סמ"ר‬78 .2 .‫ ס"מ‬13 .1 .‫ ב‬AC  32.36t 2  448t  1600 .‫) א‬14
.
SABE
 0.934 .‫ ב‬37.72 .‫) א‬17 R  13.77 .‫ג‬
SECD
C  28.9 .‫) ב‬16
‫ ס"מ‬10.1 .‫ ס"מ ב‬9.4 .‫) א‬15
. 56.89 .‫ ג‬m  16 .‫ ב‬sin  
1.5m
100  2.25m2
.‫) א‬18
.‫ ס"מ‬17.19 .‫ ס"מ ב‬4.94 .‫) א‬21 S  18.18 .‫ ג‬3 .2 1.5 28  3  t .1 .‫ ב‬4 .‫) א‬19
. BC 
. S  16cm )26
2
2 R sin  sin     
sin 
)23 DE 
1 2
b  a 2 )22 BC  10cm )21
9
S  8.641cm2 .‫ ב‬S  75.801cm2 .‫) א‬25
2
. S .‫ב‬
3
2S
 0.62S .‫) א‬29
27
SBCD
MC 
p2  q2 
pqk
)24
R
m2 tan 2  sin 45 cos 

2sin   45 
. S  37.18 .‫ ג‬44.4 , 67.78 , 67.78 .‫ב‬
)28
k
.‫) א‬31
2sin 2
. S  21.48 .‫ ג‬R  2 .‫ ב‬DE  1.6  1.26 .‫) א‬31
. SABCD  31.2 .‫ ג‬AB 
m sin    
m sin    
.‫ ב‬DC 
.‫) א‬32
3sin 
sin 
.‫ ס"מ‬63.05 .‫ ס"מ ג‬14.19 .‫ ס"מ ב‬12.75 .‫) א‬33
148
.
k 2 tan 2  sin 2
k tan 
2k 2 sin  sin 
k 2 sin  sin 
.2
.1 .‫) ב‬35 S  ‫ סמ"ר‬7.754 .‫ג‬
.‫ב‬
.‫) א‬34
2
2 tan 2
tan 2
sin    
2sin    
.‫ סמ"ר‬34.48 .‫ ס"מ ב‬7 .‫) א‬37 S  86.6 .‫ ב‬109.1 .‫) א‬36
. k  6 .‫ ג‬S 
.
k 2 sin10
k
 0.426k 2 .‫ ב‬R 
 1.21k .‫) א‬38
3
2sin 50sin 40
2sin 2 40
. S  12.52 .‫ ב‬40.72 .‫) א‬39
0.35m2 sin 2  sin 128.32   
.‫ ג‬1.27m sin  .‫ ב‬128.32 ; 51.68 .‫) א‬41
sin  25.84   
. S  172.77 .‫ ס"מ ב‬5 .‫) א‬42 k  7 .‫ ב‬BD 
.R 
k sin 20
.‫) א‬41
sin100
37
 .‫ ג‬S  ‫ סמ"ר‬18.18 .‫ ב‬AB= ‫ ס"מ‬7 - ‫ ו‬BC = ‫ ס"מ‬3 .‫) א‬43
3
. 45 , 135 .2 R  a 1 
. S  36 .‫ ב‬S  R tan 2 .‫) א‬46
2
2
 1.3a .1 .‫) ב‬44
2
a 2  5b2
‫ סמ"ר‬S  14.4 .‫ ג‬cos BCD  2
.‫) א‬45
a  3b2
. BE  7.75 .‫ ב‬58 , 58 , 64 .‫) א‬48
.  22.5 .‫ ב‬S  2R2 sin  cos  sin  90      .‫) א‬49
.   75 .‫ב‬
b sin 135   
.  26.56 .‫ ג‬S 
sin 45
,
b sin    45 
sin 45
.‫) א‬51
2R 2 cos3 
.‫ ב‬S  R 2 sin 2 .‫) א‬51
sin 
.‫ סמ"ר‬120 .‫) ג‬53   14.47 .‫ ג‬PACE  k  6k sin   k 25  24cos 2 .‫ ב‬AE  6k sin  .‫) א‬52
S  8 3 .‫) ב‬55 . S  85.57 .‫ ד‬1.72a 2 .‫ ג‬0.85a .‫ ב‬1.618a .‫) א‬54
. SABD  4 3 .2 SCDE =16 3 .1 .‫) ג‬56
. BC  0.4663m , DE  0.4663m , CD  0.4776m , BE  1.2175m .1 .‫) ד‬57
.
2
.‫ג‬
3
60 ,120 .‫) ב‬58 m  ‫ ס"מ‬8 .3 0.7232m2 .2
. B=67.38 .‫ ד‬R  13 .‫ ג‬BE  10 .‫) ב‬61
.16.73 .‫ג‬
FE  4
S ADE 16
.‫ ב‬S  81  0.25x2 .‫) א‬59

S ABC 81
.‫) ב‬62 26.56,116.56,59.19,120.8 .‫) ד‬61
149

אונ` בן – סה דנ מכינה לה – מתמטיקה גוריון

Transcription

Similar documents

דוגמא - במתמטיקה מבחן מסכם חלק א: אלגברה בסיסית

דף נוסחאות : נוסחאות הכפל ופירוק לגורמים 1. משוואה ריבועית 2. . הוא (0 פתרו

חוקי חזקות ולוגריתמים

דוגמא למבחן - אוניברסיטת תל אביב

פונקציה קווית

מלמ - שאלת רקורסיה לבחינת סיום מועד א

ThermalPhysics-Exam2010a-v1.0

פונקציה טריגונומטרית הפוכה (אינו שייך לתוכנית הלימודים)

להורדת שאלון הבחינה

2 מבחן 807 - שאלון ( )0