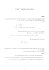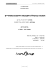מבוא לבקרה (034040)

‫'&‪."$"%-!./0$'(!'&("12' !# ()*+#(!#,"("$%&!!"%-! " !!"#$%‬‬
‫‪TECHNION — Israel Institute of Technology, Faculty of Mechanical Engineering‬‬
‫מבוא לבקרה )‪(034040‬‬
‫גליון תרגילי בית מס׳ ‪4‬‬
‫‪th2 th1‬‬
‫ציור ‪ :1‬תיאור המערכת‬
‫שאלה מס׳ ‪1‬‬
‫סטודנט תכנן מערכת המכוונת שמשיה למיקסום הצל שנוצר‪ .‬המיקום הזוויתי של השמשייה ‪ θ‬מושווה למיקום הזוויתי של השמש ‪.θ2‬‬
‫הפרש הזוויות מהווה כניסה לבקר פרופורציונלי בעל הגבר ‪ .K‬מתח היציאה מהבקר מפעיל מנוע ‪ DC‬בעל הקבועים ‪R, Kb ,KT , Jm‬‬
‫המהווים את ההתנגדות‪ ,‬קבוע המתח‪ ,‬קבוע המומנט ומומנט האינרציה בהתאמה‪ .‬המנוע מייצר מומנט אשר מניע את השמשייה‪ .‬השמשייה‬
‫בעלת מומנט אינרציה ‪ .J‬הרוח הנושבת באזור השמשייה יוצרת מומנט )‪ Td (t‬אשר פועל על השמשייה‪ .‬נתונים‪,Jm = 0.05[kg m2 ] :‬‬
‫] ‪.R = 2[Ω] ,Kb = 2[V sec] ,KT = 2[ NAm ] ,J = 1[kg m2‬‬
‫א‪ .‬ציירו דיאגרמת בלוקים מפורטת של המערכת‪.‬‬
‫)‪, θθ(s‬‬
‫ב‪ .‬רשמו את פונקציות התמסורת של החוג הסגור‬
‫)‪2 (s‬‬
‫)‪θ(s‬‬
‫)‪Td (s‬‬
‫)כתלות ב־‪.(K‬‬
‫ג‪ .‬מצאו תחום ערכי ‪ K‬עבורם המערכת בחוג הסגור יציבה‪.‬‬
‫פתרון לשאלה מס׳ ‪1‬‬
‫‪ .1‬משוואות המנוע‪:‬‬
‫•‬
‫•‬
‫•‬
‫•‬
‫˙‪V = Ri + Kb θ‬‬
‫‪Jm θ¨ = T − TL‬‬
‫‪T = KT i‬‬
‫‪Jθ¨ = TL + Td‬‬
‫משוואות התנועה של השמשייה‪:‬‬
‫‪(Jm + J)θ¨ = T + Td = KT i + Td = KT R1 V + Td − KT Kb θ˙ R1‬‬
‫‬
‫‬
‫‬
‫‬
‫‪1‬‬
‫‪KT‬‬
‫‪KT‬‬
‫‬
‫= )‪θ(s‬‬
‫‪V‬‬
‫‪+‬‬
‫‪T‬‬
‫=‬
‫)‪P(s‬‬
‫‪V‬‬
‫‪+‬‬
‫‪T‬‬
‫‪d‬‬
‫‪d‬‬
‫‪R‬‬
‫‪Jm + J s2 + KTRKb s R‬‬
‫דיאגרמת הבלוקים מתוארת בציור ‪.2‬‬
‫‪.2‬‬
‫‪KT K‬‬
‫‪R‬‬
‫‪KT K‬‬
‫‪R‬‬
‫‪KT K‬‬
‫‪R‬‬
‫‬
‫‪J s2 + KTRKb s‬‬
‫)‪θ(s‬‬
‫=‬
‫)‪θr (s‬‬
‫‪Jm +‬‬
‫‪+‬‬
‫)‪θ(s‬‬
‫‪1‬‬
‫‬
‫=‬
‫)‪Td (s‬‬
‫‪Jm + J s2 + KTRKb s +‬‬
‫‪1‬‬
‫‪θ‬‬
‫‪-‬‬
‫‬
‫‬
‫‪Td‬‬
‫‬
‫ ‬
‫?‬
‫‪V- KT‬‬
‫‪- l- K‬‬
‫)‪- l - P(s‬‬
‫‪R‬‬
‫‬‫ ‬
‫
‬
‫‪6‬‬
‫‪θr‬‬
‫ציור ‪ :2‬דיאגרמת הבלוקים‪.‬‬
‫‪ .3‬זוהי מערכת מסדר שני ⇐ יציבות אסימפטוטית כאשר )∞ ‪.K ∈ (0,‬‬
‫‬
‫ ‬
‫‬
‫‪r - l - K1 +K2 s‬‬
‫‪y‬‬‫‪10‬‬
‫‬‫‪s(s−1)+20‬‬
‫‪s‬‬
‫‬‫
‬
‫
‬
‫‬
‫‪6‬‬
‫ציור ‪ :3‬דיאגרמת הבלוקים‬
‫שאלה מס׳ ‪2‬‬
‫נתונה המערכת שמתוארת בציור ‪.3‬‬
‫‪ .1‬מהי פונקציית התמסורת ‪? yr‬‬
‫‪ .2‬מהו תחום הערכים של ‪ K2 ,K1‬עבורם המערכת בחוג סגור יציבה ?‬
‫פתרון לשאלה מס׳ ‪2‬‬
‫‪ .1‬נמצא את פה״ת מ־‪ r‬ל־‪:y‬‬
‫‪y‬‬
‫‪CP‬‬
‫)‪10(K1 + K2 s‬‬
‫‪10K2 s + 10K1‬‬
‫=‬
‫=‬
‫‪= 3‬‬
‫‪r‬‬
‫‪1 + CP‬‬
‫)‪s(s(s − 1) + 20) + 10(K1 + K2 s‬‬
‫‪s − s2 + (20 + 10K2 )s + 10K1‬‬
‫‪ .2‬הפ״א של החוג הסגור‪ .χcl = s3 − s2 + (20 + 10K2 )s + 10K1 :‬ניתן לראות שאין תחום ‪ K2 ,K1‬המייצב את המערכת בחוג‬
‫סגור )יש לחפש בקר מצורה שונה(‪.‬‬
‫שאלה מס׳ ‪3‬‬
‫נתונה פונקציית התמסורת‪:‬‬
‫‪4s‬‬
‫‪s2 +s−2‬‬
‫= )‪.G(s‬‬
‫‪ .1‬האם פונקציה זו יציבה ?‬
‫‪ .2‬הוצע לייצב את המערכת בחוג סגור באמצעות בקר פרופורציונלי ‪ .kp‬האם זה אפשרי ? אם כן מצא תחום ‪ kp‬אשר יבטיח את‬
‫יציבות החוג הסגור‪.‬‬
‫‪ .3‬הוצע לייצב את המערכת בחוג סגור באמצעות הבקר‪:‬‬
‫יבטיח את יציבות החוג הסגור‪.‬‬
‫‪ki‬‬
‫)‪s‬‬
‫‪ .C(s) = kp (1 +‬האם זה אפשרי ? אם כן מצא תחום ‪ kp‬ו־ ‪ ki‬אשר‬
‫פתרון לשאלה מס׳ ‪3‬‬
‫‪ .1‬לפה״ת יש קוטב ימני ולכן היא לא יציבה‪:‬‬
‫‪4s‬‬
‫)‪(s+2)(s−1‬‬
‫=‬
‫‪4s‬‬
‫‪s2 +s−2‬‬
‫= )‪G(s‬‬
‫‪ .2‬נרשום את הפ״א‪ .χcl (s) = 4sK + s2 + s − 2 = s2 + (4K + 1)s − 2 :‬לא ניתן לייצב מכיוון שהאיבר החופשי שלילי ללא‬
‫תלות ב־‪.K‬‬
‫‪ .3‬ישנו צמצום לא יציב בין התהליך והבקר‪ ,‬מסקנה‪ :‬לא ניתן לייצב בחוג סגור עם בקר הכולל אינטגרטור‪.‬‬
‫‪2‬‬
‫שאלה מס׳ ‪4‬‬
‫נתון התהליך‪:‬‬
‫‪1‬‬
‫‪s2 −52‬‬
‫= )‪.P(s‬‬
‫‪ .1‬האם התהליך יציב ?‬
‫‪ .2‬התהליך מחובר בחיבור טורי עם‬
‫‪s−5‬‬
‫‪s+5‬‬
‫= )‪ .C(s‬האם המערכת הכוללת יציבה ? נמק‪.‬‬
‫‪ .3‬התהליך מבוקר בחוג סגור ע״י הבקר הנתון בסעיף הקודם‪ ,‬האם החוג הסגור יציב ? נמק‪.‬‬
‫‪ .4‬התהליך מבוקר בחוג סגור ע״י בקר פרופורציונלי ‪ ,C(s) = kp‬מהו תחום ערכי ‪ kp‬עבורו החוג הסגור יציב ?‬
‫‪ .5‬התהליך מבוקר בחוג סגור ע״י בקר )‪ .C(s) = k(s + 1‬מהו תחום ערכי ‪ k‬עבורו החוג הסגור יציב אסימפטוטית ?‬
‫פתרון לשאלה מס׳ ‪4‬‬
‫‪ .1‬לפה״ת יש קוטב ימני ולכן היא לא יציבה‪:‬‬
‫‪1‬‬
‫)‪(s+5)(s−5‬‬
‫=‬
‫‪1‬‬
‫‪s2 −52‬‬
‫= )‪P(s‬‬
‫‪ .2‬לא‪ .‬לא ניתן לייצב את התהליך הלא יציב בחוג פתוח‪.‬‬
‫‪ .3‬ישנו צמצום לא יציב בין התהליך לבקר‪ ,‬מסקנה‪ :‬המערכת לא יציבה בחוג סגור‪.‬‬
‫‪ .4‬נרשום פ״א‪ .χcl = kp + s2 − 52 = s2 + 0s + kp − 25 :‬המקדם של ‪ s1‬שווה לאפס ולכן לא ניתן להשיג יציבות אסימפטוטית‬
‫ע״י בקר פרופורציונלי‪.‬‬
‫‪ .5‬נרשום את הפ״א‪ .χcl = k(s + 1) + s2 − 52 = s2 + ks + k − 25 :‬הפ״א מסדר ‪ ⇐ 2‬המערכת יציבה אסימפטוטית עבור‬
‫‪.k > 25‬‬
‫שאלה מס׳ ‪5‬‬
‫‪1‬‬
‫‪ .P(s) = s−2‬רוצים שהתהליך יפעל כמערכת ) מודל רפרנס ( יציבה מסדר שני עם מקדם ריסון‬
‫נתון תהליך בעל פונקצית התמסורת‪:‬‬
‫√‬
‫‪ ,ζ = 0.5‬תדירות תנודה מרוסנת ‪ ωd = 3‬ושגיאת מצב מתמיד אפס לכניסת מדרגה בערך הרצוי‪ .‬מוצעות האפשרויות הבאות‪:‬‬
‫‪ .1‬בקרה בחוג פתוח באמצעות חיבור טורי עם‬
‫‪ .2‬בקרה בחוג סגור עם בקר‬
‫‪ .3‬בקרה בחוג סגור עם בקר‬
‫)‪k(s−2‬‬
‫)‪s(s+a‬‬
‫‬
‫‪ki‬‬
‫‪s‬‬
‫)‪k0 (s−2‬‬
‫‪s2 +2ζωn s+ω2‬‬
‫‪n‬‬
‫= )‪.C(s‬‬
‫= )‪.C(s‬‬
‫‪.C(s) = kp 1 +‬‬
‫עבור כל אחד מהמקרים הנ״ל‪:‬‬
‫א‪ .‬מצא את הפרמטרים הדרושים‪.‬‬
‫ב‪ .‬חשב את השגיאה במצב מתמיד להפרעת מדרגה בכניסה לתהליך‪.‬‬
‫ג‪ .‬הבע דעתך על היתרונות והחסרונות שלו‪.‬‬
‫פתרון לשאלה מס׳ ‪5‬‬
‫נמצא את ‪:ωn‬‬
‫‪1 − ζ2‬‬
‫נבחר את מודל הרפרנס להיות‬
‫‪p‬‬
‫‪ωd = ωn‬‬
‫⇐‬
‫‪=2‬‬
‫‪bs + 4‬‬
‫‪,‬‬
‫‪s2 + 2s + 4‬‬
‫√‬
‫‪3‬‬
‫√‬
‫‪1−0.25‬‬
‫=‬
‫‪ωn = √ωd‬‬
‫‪1−ζ2‬‬
‫= )‪Tyr (s‬‬
‫כאשר ‪ b‬הינו פרמטר כלשהו‪.‬‬
‫‪ .1‬לא ניתן לייצב את התהליך בחוג פתוח‪ ,‬ז״א ∞ = ‪.ess‬‬
‫‪ .2‬קל לראות שעבור כל בחירה של פרמטרי הבקר‪ ,‬קיים צמצום בין קוטב לא יציב של התהליך ואפס של הבקר‪ .‬לכן‪ ,‬עבור כל‬
‫בחירת פרמטרים‪ ,‬המערכת בחוג סגור אינה יציבה פנימית‪ .‬שוב‪.ess = ∞ ,‬‬
‫‪3‬‬
‫‪ .3‬פונקציית התמסורת שמקשרת בין ‪ r‬ל־‪ y‬במערכת בקרה בחוג סגור הינה‬
‫‪kp s+kp ki‬‬
‫‪k p s + k p ki‬‬
‫)‪y(s‬‬
‫)‪P(s)C(s‬‬
‫)‪s(s−2‬‬
‫‪= 2‬‬
‫=‬
‫=‬
‫‪k‬‬
‫‪s+k‬‬
‫‪k‬‬
‫‪p‬‬
‫‪p‬‬
‫‪i‬‬
‫)‪r(s‬‬
‫)‪1 + P(s)C(s‬‬
‫‪s + (kp − 2)s + kp ki‬‬
‫)‪1 + s(s−2‬‬
‫מהשוואה עם מודל הרפרנס נקבל‬
‫‪ki = 1‬‬
‫כלומר‬
‫נבדוק את הפולינום האופייני‪:‬‬
‫‪kp = 4,‬‬
‫‬
‫‬
‫‪4s + 4‬‬
‫‪1‬‬
‫=‬
‫‪C(s) = 4 1 +‬‬
‫‪s‬‬
‫‪s‬‬
‫‪χcl = s(s − 2) + (4s + 4) = s2 + 2s + 4‬‬
‫המערכת יציבה בחוג סגור )אכן ניתן ליישם אותה(‪.‬‬
‫‪4‬‬