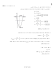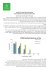פתרון שאלון 802 קיץ תשע"ה 2015, מועד א

‫‪1‬‬
‫בגרות עה מאי ‪ 15‬מועד קיץ א שאלון ‪35802‬‬
‫א‪ .‬נתונה הפרבולה שמשוואתה ‪. y   x 2  4 x  7‬‬
‫נציב ‪ , x  0‬על מנת למצוא את שיעורי נקודת החיתוך עם ציר ה‪: y -‬‬
‫‪ , y  02  4  0  7  7‬ובהתאם‪. (0, - 7) :‬‬
‫נציב ‪ y  0‬במשוואת הפרבולה‪ ,‬על מנת למצוא את שיעורי נקודות החיתוך עם ציר ה‪. x -‬‬
‫‪0   x2  4x  7‬‬
‫)‪4  42  4  (1)  (7‬‬
‫)‪2  (1‬‬
‫‪x1,2 ‬‬
‫‪4  12‬‬
‫‪2‬‬
‫‪x1,2 ‬‬
‫המספר שבתוך השורש שלילי ולכן אין פתרון‪.‬‬
‫אין נקודות חיתוך עם ציר ה‪ , x -‬כפי שניתן לראות בסרטוט‪.‬‬
‫תשובה‪. (0, - 7) :‬‬
‫ב‪ .‬הפונקציה שלילית לכל ‪) x‬הפרבולה מתחת לציר ה‪.( x -‬‬
‫‪b‬‬
‫ג‪ .‬נמצא את שיעורי קדקוד הפרבולה‪ ,‬על פי הנוסחה‪:‬‬
‫‪2a‬‬
‫‪4‬‬
‫‪2‬‬
‫)‪2  (1‬‬
‫‪‬‬
‫‪‬‬
‫)‪ (2,  3‬‬
‫‪ 22  4  2  7  3‬‬
‫‪. xkodkod  ‬‬
‫‪xkodkod ‬‬
‫‪xkodkod‬‬
‫תשובה‪ :‬שיעורי קדקוד הפרבולה הם )‪. (2,  3‬‬
‫ד‪ .‬הפרבולה עולה עד לקדקוד‪ ,‬כלומר עבור ‪- x‬ים קטנים מ‪. 2 -‬‬
‫תשובה‪. x  2 :‬‬
‫נכתב ע"י עפר ילין‬
‫‪2‬‬
‫בגרות עה מאי ‪ 15‬מועד קיץ א שאלון ‪35802‬‬
‫א‪ .‬נתונים כל המספרים הדו‪ -‬ספרתיים‪. 10, 11, 12,...,99 :‬‬
‫אם נוריד את ‪ 9‬המספרים החד‪-‬ספרתיים ) ‪ ( 1, 2, 3,...,9‬מ‪ 99 -‬המספרים ‪, 1, 2, 3,...,99‬‬
‫אז קל לראות שיש ‪ 90‬מספרים דו‪ -‬ספרתיים‪.‬‬
‫דרך פתרון אחרת‪:‬‬
‫‪99  10  (n  1) 1‬‬
‫‪99  10  n  1‬‬
‫‪99  9  n‬‬
‫‪90  n‬‬
‫תשובה‪ :‬יש ‪ 90‬מספרים דו‪-‬ספרתיים‪.‬‬
‫ב‪ (1) .‬המספר הדו‪ -‬ספרתי הקטן ביותר שמחלק ב‪) 5 -‬בלי שארית( הוא ‪. 10‬‬
‫)‪ (2‬המספר הדו‪ -‬ספרתי הגדול ביותר שמחלק ב‪) 5 -‬בלי שארית( הוא ‪. 95‬‬
‫)‪ (3‬סדרת המספרים הדו‪ -‬ספרתיים‪ ,‬המחלקים ב‪) 5 -‬בלי שארית( היא סדרה חשבונית‪ ,‬שבה ‪. d  5‬‬
‫נמצא את מספר איברי הסדרה‪ ,‬כאשר ‪. d  5 an  95 , , a1  10 ,‬‬
‫בסיוע נוסחת האיבר הכללי‪an  a1  (n  1)d :‬‬
‫‪an  a1  (n  1)d‬‬
‫‪95  10  ( n  1)  5‬‬
‫‪95  10  5n  5‬‬
‫‪95  5  5n‬‬
‫‪90  5n‬‬
‫‪n  18‬‬
‫תשובה‪ 18 :‬מספרים דו‪ -‬ספרתיים מתחלקים ב‪ 5 -‬בלי שארית‪.‬‬
‫ג‪ .‬יש ‪ 90‬מספרים דו‪ -‬ספרתיים‪.‬‬
‫מתוכם ‪ 18‬מספרים דו‪ -‬ספרתיים מתחלקים ב‪ 5 -‬בלי שארית‪.‬‬
‫לכן ‪ 90  18  72‬מספרים דו‪-‬ספרתיים אינם מתחלקים ב‪ 5 -‬בלי שארית‪.‬‬
‫תשובה‪ 72 :‬מספרים דו‪-‬ספרתיים אינם מתחלקים ב‪ 5 -‬בלי שארית‪.‬‬
‫נכתב ע"י עפר ילין‬
‫‪3‬‬
‫בגרות עה מאי ‪ 15‬מועד קיץ א שאלון ‪35802‬‬
‫האוכלוסייה בעיר גדֵ לה באופן מעריכי‪.‬‬
‫הגרף שלפנינו מתאר את גידול האוכלוסייה‬
‫מתחילת שנת ‪ 1980‬עד תחילת שנת ‪.1983‬‬
‫א‪ (1) .‬מספר התושבים בעיר‪ ,‬בתחילת ‪ , 1980‬היה ‪ 40, 000‬על פי נקודת החיתוך של הגרף עם הציר האנכי‪.‬‬
‫)‪ (2‬מספר התושבים בעיר‪ ,‬בתחילת ‪ , 1983‬היה ‪ 69,120‬על פי הנקודה הימנית בגרף‪.‬‬
‫ב‪ .‬נחשב בכמה אחוזים ג ְֵדלה אוכלוסיית העיר מדי שנה‪.‬‬
‫גודל האוכלוסייה ההתחלתי הוא ‪ 40, 000‬תושבים וכעבור ‪ 3‬שנים הוא ‪ 69,120‬תושבים‪.‬‬
‫‪/ : 40, 000‬‬
‫‪69,120  40, 000  q3‬‬
‫‪t‬‬
‫‪q‬‬
‫‪M0‬‬
‫‪Mt‬‬
‫‪69,120‬‬
‫‪ q3‬‬
‫‪40, 000‬‬
‫‪3‬‬
‫?‬
‫‪40, 000‬‬
‫‪69,120‬‬
‫‪1.728  q3‬‬
‫‪q  3 1.728‬‬
‫‪q  1.2‬‬
‫‪100  P‬‬
‫‪/ 100‬‬
‫‪100‬‬
‫‪120  100  P / 100‬‬
‫‪1.2 ‬‬
‫‪P  20%‬‬
‫תשובה‪ :‬האוכלוסייה ג ְֵדלה מדי שנה ב‪. 20% -‬‬
‫נכתב ע"י עפר ילין‬
‫ג‪ .‬נמצא מה היה מספר התושבים בעיר בתחילת שנת ‪ , 1984‬כלומר ‪ 4‬שנים מתחילת שנת ‪, 1980‬‬
‫בהנחה שקצב הגידול אינו משתנה‪.‬‬
‫‪M 4  40, 000 1.24‬‬
‫‪t‬‬
‫‪q‬‬
‫‪M0‬‬
‫‪Mt‬‬
‫‪M 4  82,944‬‬
‫‪4‬‬
‫‪1.2‬‬
‫‪40, 000‬‬
‫?‬
‫תשובה‪ :‬מספר התושבים בעיר‪ ,‬בתחילת שנת ‪ , 1984‬היה ‪. 82,944‬‬
‫ד‪ .‬נמצא מה היה בערך מספר התושבים בעיר בתחילת שנת ‪ , 1978‬כלומר ‪ 2‬שנים לפני תחילת שנת ‪. 1980‬‬
‫בהנחה שקצב הגידול אינו משתנה‪.‬‬
‫‪/ :1.22‬‬
‫‪40, 000  M 0 1.22‬‬
‫‪40, 000‬‬
‫‪ M0‬‬
‫‪1.22‬‬
‫‪M 0  27, 778‬‬
‫‪t‬‬
‫‪q‬‬
‫‪M0‬‬
‫‪Mt‬‬
‫‪2‬‬
‫‪1.2‬‬
‫?‬
‫‪40, 000‬‬
‫תשובה‪ :‬מספר התושבים בעיר‪ ,‬בתחילת שנת ‪ , 1978‬היה בערך ‪ 27, 778‬תושבים‪.‬‬
‫נכתב ע"י עפר ילין‬
‫‪4‬‬
‫בגרות עה מאי ‪ 15‬מועד קיץ א שאלון ‪35802‬‬
‫א‪ .‬נחשב את האורך של האלכסון ‪. BD‬‬
‫‪DNB‬‬
‫‪9‬‬
‫‪BD‬‬
‫‪BD cos 32 = 9‬‬
‫= ‪cos 32‬‬
‫‪9‬‬
‫‪cos 32‬‬
‫‪BD ‬‬
‫‪ 10.61‬ס"מ ‪BD ‬‬
‫תשובה‪ :‬אורך האלכסון ‪ BD‬הוא ‪ 10.61‬ס"מ‪.‬‬
‫ב‪NDB  180  90  32  58 (1) .‬‬
‫תשובה‪. NDB  58 :‬‬
‫)‪ (2‬צלעות המעוין שוות זו לזו‪ ,‬לכן ‪ CBD‬הוא שווה שוקיים )‪ (CB  CD‬וזוויות הבסיס שוות זו לזו‪.‬‬
‫‪CBD  NDB  58‬‬
‫‪C  180  58  58  64‬‬
‫תשובה‪. C  64 , CBD  58 :‬‬
‫ג‪ .‬נחשב את האורך של צלע המעוין‪.‬‬
‫‪CNB‬‬
‫‪9‬‬
‫‪CB‬‬
‫‪CBsin 64 = 9‬‬
‫= ‪sin 64‬‬
‫‪9‬‬
‫‪sin 64‬‬
‫= ‪CB‬‬
‫‪ 10.01‬ס"מ = ‪CB‬‬
‫תשובה‪ :‬אורך צלע המעוין הוא ‪ 10.01‬ס"מ‪.‬‬
‫נכתב ע"י עפר ילין‬
‫‪5‬‬
‫בגרות עה מאי ‪ 15‬מועד קיץ א שאלון ‪35802‬‬
‫א‪ .‬האלכסון ‪ AC‬של בסיס הפירמידה הריבועית הוא ‪ 329.5‬מטר‪.‬‬
‫נחשב את צלע הריבוע של בסיס הפירמידה‪ ,‬שנסמנה ב‪, x -‬‬
‫באמצעות משפט פיתגורס‪.‬‬
‫‪ABC‬‬
‫‪(AC) 2  (AB) 2  (BC) 2‬‬
‫‪329.52  x 2  x 2‬‬
‫‪329.52  2 x 2‬‬
‫‪/:2‬‬
‫‪/‬‬
‫‪54285  x 2‬‬
‫‪ 233‬מטר ‪x ‬‬
‫תשובה‪ :‬המרחק שהתייר עבר‪ ,‬מנקודה ‪ A‬לנקודה ‪ , B‬הוא ‪ 233‬מטר‪.‬‬
‫ב‪ .‬כיוון שצלעות הריבוע שוות זו לזו‪,‬‬
‫הרי שהתייר עבר מרחק של ‪ 932‬מטר ‪. 233  4 ‬‬
‫תשובה‪ :‬סך כל המרחק שהתייר עבר‪ ,‬מנקודה ‪ A‬ועד חזרתו לנקודה ‪ , A‬הוא ‪ 932‬מטר‪.‬‬
‫ג‪ .‬נחשב את הזווית שבין המקצוע ‪ SC‬לבסיס הפירמידה‪. SCH ,‬‬
‫הגובה ‪ SH‬של הפירמידה הוא ‪ 329.5‬מטר‪.‬‬
‫בסיס הפירמידה הוא ריבוע‪ H ,‬היא נקודת מפגש האלכסונים‪ ,‬החוצים זה את זה‪.‬‬
‫‪AC 329.5‬‬
‫‪‬‬
‫‪ 164.75‬מטר ‪‬‬
‫‪2‬‬
‫‪2‬‬
‫‪CH ‬‬
‫‪SCH‬‬
‫‪SH‬‬
‫‪CH‬‬
‫‪137‬‬
‫‪tan SCH ‬‬
‫‪164.75‬‬
‫‪SCH  39.75‬‬
‫‪tan SCH ‬‬
‫תשובה‪ :‬הזווית בין המקצוע ‪ SC‬לבסיס הפירמידה היא בת ‪. 39.75‬‬
‫נכתב ע"י עפר ילין‬
‫‪6‬‬
‫בגרות עה מאי ‪ 15‬מועד קיץ א שאלון ‪35802‬‬
‫א‪ .‬בבחינה במתמטיקה בכיתה יב התפלגו הציונים כך‪:‬‬
‫הציון‬
‫‪60‬‬
‫‪70‬‬
‫‪80‬‬
‫‪90‬‬
‫מספר התלמידים‬
‫‪7‬‬
‫‪x‬‬
‫‪11‬‬
‫‪1‬‬
‫מספר התלמידים הכולל הוא סכום השכיחויות‪N  f1  f 2  ...  f n :‬‬
‫‪N  7  x  11  1‬‬
‫‪N  19  x‬‬
‫ממוצע הציונים בכיתה היה ‪. 72.5‬‬
‫‪x1 f1  x1 f1  ...  xn f n‬‬
‫נשתמש בנוסחה למציאת ממוצע ‪:‬‬
‫‪N‬‬
‫‪x‬‬
‫‪60  7  70  x  80 11  90 1‬‬
‫)‪/ (19  x‬‬
‫‪19  x‬‬
‫‪72.5(19  x)  1390  70 x‬‬
‫‪1377.5  72.5 x  1390  70 x‬‬
‫‪2.5 x  12.5 / : 2.5‬‬
‫‪12.5‬‬
‫‪x‬‬
‫‪2.5‬‬
‫‪x5‬‬
‫‪72.5 ‬‬
‫תשובה‪. x  5 :‬‬
‫נכתב ע"י עפר ילין‬
‫ב‪ .‬נעדכן את טבלת השכיחויות‪.‬‬
‫מספר התלמידים שנבחנו בבחינה הוא ‪. 1  11  5  7  24‬‬
‫הציון‬
‫‪60‬‬
‫‪70‬‬
‫‪80‬‬
‫‪90‬‬
‫מספר התלמידים‬
‫‪7‬‬
‫‪5‬‬
‫‪11‬‬
‫‪1‬‬
‫שכיחות מצטברת‬
‫‪7‬‬
‫‪12‬‬
‫‪23‬‬
‫‪24‬‬
‫‪n 24‬‬
‫‪‬‬
‫מספר התלמידים הוא זוגי‪ ,‬כאשר‪ 12 :‬‬
‫‪2 2‬‬
‫לכן החציון יהיה ממוצע ציוני התלמידים שבמקום ה‪ 12 -‬וה‪, 13 -‬‬
‫כאשר מסדרים את הציונים בסדר עולה‪.‬‬
‫‪70  80‬‬
‫נחשב את החציון‪ 75 :‬‬
‫‪2‬‬
‫‪.‬‬
‫תשובה‪ :‬חציון הציונים הוא ‪. 75‬‬
‫ג‪ .‬הציון השכיח הוא הציון שהתקבל מספר הפעמים הרב ביותר‪ ,‬כלומר הציון ‪. 80‬‬
‫תשובה‪ :‬הציון השכיח הוא ‪. 80‬‬
‫ד‪ .‬מספר התלמידים שקבלו ציון נמוך מהממוצע ) ‪ ( 72.5‬הוא ‪. 7  5  12‬‬
‫‪12‬‬
‫ההסתברות‪ ,‬כאשר בוחרים תלמיד באקראי‪ ,‬שהציון יהיה ציון נמוך מהממוצע היא ‪ 0.5‬‬
‫‪24‬‬
‫תשובה‪ :‬ההסתברות היא ‪. 0.5‬‬
‫ה‪ .‬ציונו של התלמיד החדש‪ ,‬שווה בדיוק לממוצע הקיים‪. 72.5 ,‬‬
‫לכן‪ ,‬פיזור הנתונים קָ טֵ ן‪ ,‬כי הם מרוכזים יותר סביב הממוצע‪.‬‬
‫סטיית התקן קְ טֵ נּה‪ ,‬כי היא מדד של פיזור הנתונים‪.‬‬
‫תשובה‪ :‬סטיית התקן קְ טֵ נּה‪.‬‬
‫נכתב ע"י עפר ילין‬
‫‪.‬‬