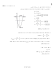דף ניווט-שלבים בחקירת פונקציה

‫שלבים בחקירת פונקציה‬
‫ניקח לדוגמא את הפונקציה ‪f(x) = -x2 – 2x + 15‬‬
‫שם שלב‬
‫שלב‬
‫‪.1‬‬
‫הסבר‬
‫חילוץ מקדמי‬
‫נרשום את מקדמי האיברים במשוואה הריבועית על פי‬
‫המשוואה‬
‫התבנית‪:‬‬
‫דוגמא‬
‫‪f(x) = -x2 – 2x + 15‬‬
‫‪ax2 + bx + c‬‬
‫הריבועית‬
‫‪a = -1‬‬
‫‪b = -2‬‬
‫‪ = a‬מקדם של ‪x2‬‬
‫‪c = 15‬‬
‫‪ = b‬מקדם של ‪x‬‬
‫‪ = c‬מספר‬
‫‪.2‬‬
‫מציאת כיוון‬
‫הפרבולה‬
‫‪2‬‬
‫אם ‪ ,a‬המקדם של ‪ , x‬חיובי – הפרבולה ישרה (מחייכת)‪.‬‬
‫‪a = -1‬‬
‫‪2‬‬
‫אם ‪ ,a‬המקדם של ‪ , x‬שלילי – הפרבולה הפוכה (בוכה)‪.‬‬
‫‪ a < 0‬לכן הפרבולה תהייה פרבולה‬
‫הפוכה‬
‫‪.3‬‬
‫מציאת‬
‫קודקוד‬
‫נמצא את ערכי נקודת קודקוד הפרבולה‪:‬‬
‫‪‬‬
‫הפרבולה‬
‫בתחילה נמצא את ערך ה – ‪ X‬ע"י שימוש בנוסחא‪:‬‬
‫‪b‬‬
‫‪2a‬‬
‫‪‬‬
‫=‬
‫‪x‬קוד‬
‫=‬
‫‪b‬‬
‫‪2a‬‬
‫‪= 2*21‬‬
‫‪x‬קוד‬
‫‪x‬קוד‬
‫‪= -1‬‬
‫לאחר מציאת ערך ה‪ x -‬נציב אותו במשוואה‬
‫‪x‬קוד‬
‫נציב את הערך ה‪ X -‬במשוואה‬
‫המקורית ונמצא את ערך ה ‪.y‬‬
‫‪f(x) = -x2 – 2x + 15‬‬
‫נקבל ‪ f(x) = 11‬כלומר‪ ,‬ערך ה‪ Y -‬הוא‬
‫‪ .11‬נקודת קודקוד הפרבולה )‪(-1 , 16‬‬
‫‪.4‬‬
‫מציאת‬
‫נקודת חיתוך‬
‫עם ציר ה‪Y-‬‬
‫בנקודה בה הפרבולה חותכת את ציר ה‪ ,Y-‬ערך ה – ‪ X‬שווה‬
‫ל‪.0-‬‬
‫כדי למצוא את הנקודה בה הפונקציה‪/‬פרבולה חותכת את‬
‫ציר ה – ‪ Y‬נציב במקום ‪ X‬את הערך ‪0‬‬
‫‪f(x) = -x2 – 2x + 15‬‬
‫נציב ‪x=0‬‬
‫‪F(x) = 15‬‬
‫כלומר הפונקציה‪/‬הפרבולה חותכת את‬
‫ציר ה ‪ Y‬בנקודה ‪11‬‬
‫משה בר – הוראת מתמטיקה | ‪| www.agurim.co.il‬‬
‫‪| 240-1543446‬‬
‫‪[email protected]‬‬
‫| עמוד‪6‬‬
‫‪ .1‬מציאת נקודת‬
‫החיתוך עם ציר‬
‫ה‪X-‬‬
‫בנקודה בה הפרבולה חותכת את ציר ה‪ X -‬ערך ה –‪ Y‬שווה‬
‫ל‪.0-‬‬
‫נשווה את הפונקציה ל‪ 0-‬ונפתור משוואה ריבועית על פי‬
‫הנוסחא‪:‬‬
‫‪ .1‬מציאת תחום‬
‫חיוביות‪/‬שליליות‬
‫הפונקציה חיובית כאשר היא נמצאת מעל ציר ‪)0>Y ( X‬‬
‫‪f(x) = -x2 – 2x + 15‬‬
‫‪a = -1‬‬
‫‪b = -2‬‬
‫‪c = 15‬‬
‫נציב את המשתנים ‪ a, b c‬בנוסחאת‬
‫המשוואה הריבועית ונמצא את ערכי ‪X‬‬
‫אלו הן הנקודות בהן הפונקציה‪/‬הפרבולה‬
‫חותכת את ציר ה ‪ x‬כמופיע בשרטוט‪.‬‬
‫יתכן מצב בו הפרבולה חותכת את ציר ה‪-‬‬
‫‪ X‬בשתי נקודות‪.‬‬
‫יתכן מצב בו למשוואה הריבועית יש רק‬
‫פתרון אחד ואז הפרבולה נוגעת רק‬
‫בנקודה אחת בציר ה‪.X -‬‬
‫יתכן מצב בו אין פתרון למשוואה‬
‫הריבועית אזי הפרבולה לא נוגעת כלל‬
‫בציר ‪.X‬‬
‫הפונקציה שלילית כאשר נמצאת מתחת לציר ‪)0 <Y ( X‬‬
‫‪ .7‬מציאת תחום‬
‫עליה וירידה‬
‫תחומי עליה וירידה נקבעים על פי צורת הפרבולה‪:‬‬
‫‪‬‬
‫בפרבולה ישרה (מחייכת) תחום העלייה יהיה כאשר‬
‫‪ X‬גדול מנקודת ה ‪ X‬של קודקוד הפרבולה ותחום‬
‫הירידה כאשר ‪ X‬קטן מנקודת ‪ X‬של הפרבולה‪.‬‬
‫‪‬‬
‫בפרבולה הפוכה (בוכה) תחום העלייה יהיה כאשר‬
‫‪ X‬קטן מנקודת ה ‪ X‬של קודקוד הפרבולה ותחום‬
‫הירידה כאשר ‪ X‬גדול מנקודת ‪ X‬של קודקוד‬
‫הפרבולה‪.‬‬
‫משה בר – הוראת מתמטיקה | ‪| www.agurim.co.il‬‬
‫‪| 240-1543446‬‬
‫‪[email protected]‬‬
‫| עמוד‪0‬‬