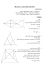ל"חי 5 לקראת כיתה י` – ד עבודת קיץ תשע;quot& פרק ראשון: פונקציות ריבועיו

‫עבודת קיץ תשע"ד – לקראת כיתה י' ‪ 5‬יח"ל‬
‫פרק ראשון‪ :‬פונקציות ריבועיות‬
‫שאלה ‪:1‬‬
‫לפניך רשימת פונקציות ריבועיות ורשימת תכונות‪.‬‬
‫א‪ .‬עבור כל פונקציה בחר את כל התכונות מהרשימה שמתאימות לה‪ .‬נמק בחירותיך‪.‬‬
‫ב‪ .‬איזוהי התכונה המופיעה בטבלה שאין לה פונקציה מתאימה? הסבר‪.‬‬
‫פונקציות‬
‫תכונות‬
‫‪y = 3(x + 2)2‬‬
‫א‪.‬‬
‫שיעור ה‪ x -‬של הקדקוד הוא ‪–2‬‬
‫‪y = –(x + 2)2‬‬
‫ב‪.‬‬
‫שיעורי הקדקוד (‪)0 , –4‬‬
‫‪y = (x – 2)2‬‬
‫ג‪.‬‬
‫ציר הסימטריה עובר בנקודה (‪)–1 , 3‬‬
‫‪y = 3x2– 1‬‬
‫ד‪.‬‬
‫ציר הסימטריה הוא‪x = 2 :‬‬
‫‪y = 2(x + 1)2 + 3‬‬
‫ה‪.‬‬
‫הפרבולה בעלת מינימום‬
‫‪y = –x2 + 3‬‬
‫ו‪.‬‬
‫זרועות הפרבולה פתוחות ביחס לפרבולה‪y = 2x2 :‬‬
‫‪y= –2x2 – 4‬‬
‫ז‪.‬‬
‫לפרבולה יש שתי נקודות חיתוך עם הישר‪y =(– 1) :‬‬
‫‪y = 3x2 – 4‬‬
‫ח‪.‬‬
‫לפרבולה אין נקודות חיתוך עם ציר ה‪.x-‬‬
‫‪y = 3(x – 4)2‬‬
‫ט‪.‬‬
‫ציר הסימטריה של הפרבולה הוא ציר ה‪.y-‬‬
‫‪y = 2x2‬‬
‫י‪.‬‬
‫הפרבולה עוברת בנקודה )‪(– 1,2‬‬
‫‪2‬‬
‫‪y=   (x – 2)2‬‬
‫‪9‬‬
‫שאלה ‪:2‬‬
‫יא‪ .‬הפרבולה לא חותכת את הישר‪x =10 :‬‬
‫שאלה ‪:3‬‬
‫הביטו בשרטוט הבא‪:‬‬
‫הגרף המתואר הוא פרבולה‪ ,‬כלומר מתאים לפונקציה‬
‫ריבועית‪.‬‬
‫משוואת הישר המתואר בשרטוט היא‪.y=10 :‬‬
‫על‪-‬פי הנתונים שבשרטוט ענו על השאלות הבאות‪:‬‬
‫א‪ .‬מהו הערך של ‪? k‬‬
‫ב‪ .‬מהם שיעורי הנקודות ‪ A‬ו‪? B-‬‬
‫ג‪ .‬אילו מהביטויים הבאים יכולים להתאים‬
‫לגרף של הפונקציה הריבועית?‬
‫נמק תשובותיך‪.‬‬
‫(‪f ( x)  x 2  6 x  5 )1‬‬
‫(‪f ( x)  (5  x)( x  1) )2‬‬
‫(‪f ( x)  (2 x  2)( x  5) )3‬‬
‫(‪f ( x)  ( x  1)( x  10) )4‬‬
‫(‪f ( x)  2 x 2  12 x  10 )5‬‬
‫ד‪ .‬מהם שיעורי הקדקוד של הפונקציה?‬
‫ה‪ .‬לגבי כל אחת מהטענות הבאות רשמו אם היא נכונה או לא‪ .‬אם אינה‬
‫נכונה – תקנו אותה‪ .‬נמקו היטב‪.‬‬
‫(‪ )1‬הפונקציה‪ g ( x)  x 2  6 x  5 :‬חותכת את הפונקציה שבשרטוט‬
‫בדיוק בשתי נקודות‪.‬‬
‫(‪ )2‬בנקודה שבה ‪ x=2‬הפונקציה עולה‪.‬‬
‫(‪f (5)  f (7)  0 )3‬‬
‫(‪ f ( x)  (8) )4‬לכל ערך של ‪. x‬‬
‫שאלה ‪:4‬‬
‫שאלה ‪:5‬‬
‫הצלעות של המרובע ‪ ABCO‬מונחות על‪:‬‬
‫ציר ה‪ ,x -‬הישר ‪ ,y = x‬הישר ‪ ,y = x – 5‬הישר ‪.a > 5 x = a‬‬
‫א‪ .‬איזה מרובע הוא ‪ ?ABCO‬נמקו‪.‬‬
‫ב‪ .‬הציעו ערך מתאים לפרמטר ‪ a‬וציינו את שיעורי‬
‫הקדקודים‪D ,C ,B ,A :‬‬
‫‪C‬‬
‫ב‪.‬‬
‫על פי ערך ה‪ a -‬שקבעתם‪:‬‬
‫(‪ )1‬חשבו את שטח המשולש ‪ABD‬‬
‫(‪ )2‬חשבו את שטח המשולש ‪ADC‬‬
‫‪B‬‬
‫(‪ )3‬חשבו את שטח המרובע ‪ABCO‬‬
‫ג‪.‬‬
‫מצאו את הערך של ‪ a‬אם ידוע ששטח המרובע ‪ ABCO‬שווה‬
‫‪ 22.5‬יחידות ריבועיות‪.‬‬
‫הציגו את דרך הפתרון‪.‬‬
‫ד‪ .‬מצאו משוואה של פרבולה שקדקודה בנקודה ‪ C‬ועוברת בנקודה ‪.O‬‬
‫‪D‬‬
‫‪A‬‬
‫‪O‬‬
‫פרק שני‪ :‬טכניקה אלגברית‪ :‬חזקות ופונקציות ריבועיות‬
‫‪ .I‬פתור את המשוואות הבאות – משוואות עם שברים אלגבריים‪.‬‬
‫‪x 1‬‬
‫‪x2‬‬
‫‪1‬‬
‫‪ 2‬‬
‫‪‬‬
‫(‪)1‬‬
‫‪x  7 x x  49 2 x  14‬‬
‫(‪)2‬‬
‫‪2‬‬
‫‪9 x‬‬
‫‪1‬‬
‫‪1‬‬
‫‪ 2‬‬
‫‪‬‬
‫‪x  2x  1 x  1 x  1‬‬
‫‪2‬‬
‫‪1 x‬‬
‫‪6x  1‬‬
‫‪x‬‬
‫‪ 2‬‬
‫‪‬‬
‫(‪)3‬‬
‫‪3  2x 2x  x  3 x  1‬‬
‫‪ .II‬פתור את המשוואות הפרמטריות הבאות (הבע את הפתרון באמצעות הפרמטר ‪:) a‬‬
‫‪x‬‬
‫‪a‬‬
‫‪x  a2‬‬
‫‪‬‬
‫‪‬‬
‫(‪)1‬‬
‫‪6  a 6  a 36 a 2‬‬
‫‪1‬‬
‫‪2‬‬
‫‪2‬‬
‫‪ 2‬‬
‫‪‬‬
‫(‪)2‬‬
‫‪2‬‬
‫‪2 x  2a x  2ax  a‬‬
‫‪ax  a 2‬‬
‫(‪ )3‬פתור את המשוואה הבאה‪(m  1) x 2  2mx  m  1  0 :‬‬
‫‪m6‬‬
‫‪mx 2  3x ‬‬
‫(‪ )4‬פתור את המשוואה הבאה‪ 0 :‬‬
‫‪4‬‬
‫‪x  1 2a  1‬‬
‫‪‬‬
‫(‪ )5‬פתור את המשוואה הבאה‪ 1 :‬‬
‫‪a‬‬
‫‪x‬‬
‫‪ .III‬פתור את המשוואות הבאות‪:‬‬
‫בני גורן ‪ 404-408‬חלק א' עמוד ‪ 104,108‬תרגילים‪.12 ,24 ,8 :‬‬
‫‪.IV‬‬
‫(‪)1‬‬
‫(‪)2‬‬
‫(‪)3‬‬
‫(‪)4‬‬
‫(‪)5‬‬
‫אי‪-‬שיוויונות ריבועיים‪.‬‬
‫פתור את האי‪-‬שוויון הבא‪2 x  3x  1  0 :‬‬
‫פתור את האי‪-‬שוויון הבא‪ x 2  3x  10  0 :‬‬
‫פתור את האי‪-‬שוויון הבא‪x( x  12)  2( x  24) :‬‬
‫מצא לאילו ערכי ‪ x‬גרף הפונקציה ‪ y  x 2  4 x‬נמצא מתחת לישר ‪ y  x  4‬ומעל לישר‬
‫‪. y  x6‬‬
‫בני גורן ‪ 404-408‬חלק א' – עמ' ‪ 131‬תרגילים‪.34 ,33 ,38 :‬‬
‫‪2‬‬
‫‪ .V‬פתור את התרגילים הבאים בנושא‪ :‬חוקי חזקות‪ :‬בני גורן ‪ 404-408‬חלק א' לפי הפירוט‪:‬‬
‫עמוד ‪20‬‬
‫תרגילים‪20 ,13 ,14 :‬‬
‫עמוד ‪21‬‬
‫תרגילים‪53 ,54 ,45 ,44 ,35 ,32 :‬‬
‫עמוד ‪23‬‬
‫תרגילים‪32 ,30 ,28 ,22 ,14 ,14 ,10 ,8 ,2 :‬‬
‫עמוד ‪23‬‬
‫תרגילים‪43 ,40 :‬‬
‫עמוד ‪24‬‬
‫תרגילים‪53 ,51 :‬‬
‫‪ .VI‬פרק שלישי‪ :‬גיאומטריה‬
‫שאלה ‪:1‬‬
‫בריבוע ‪ ABCD‬שאורך צלעו ‪ 4‬ס"מ‪ ,‬סימנו נקודה ‪ O‬שמרחקה‬
‫מהצלע ‪ AB‬שווה למרחקיה מהקדקודים ‪ C‬ו‪ .D-‬כלומר‪:‬‬
‫‪.DO=CO=EO‬‬
‫חשב את סכום האורכים ‪. EO+CO+DO :‬‬
‫שאלה ‪:2‬‬
‫‪ EF , DE‬קטעי אמצעים במשולש ‪.ABC‬‬
‫הנקודה ‪ G‬היא נקודת החיתוך של הקטעים ‪ ED‬ו‪.BF -‬‬
‫א‪ .‬אילו מהטענות הבאות נכונות תמיד?‬
‫‪EG = DG‬‬
‫‪.I‬‬
‫‪ BF‬תיכון לצלע ‪AC‬‬
‫‪.II‬‬
‫‪FD  AB‬‬
‫‪.III‬‬
‫‪2  GE = FC‬‬
‫‪.IV‬‬
‫ב‪ .‬הוכיחו את הטענות הנכונות‪.‬‬
‫שאלה ‪:3‬‬
‫פתור את השאלות הבאות מהספר‪ :‬בני גורן ‪ 404-408‬חלק א'‬
‫עמוד‬
‫תרגילים‬
‫‪254‬‬
‫‪4‬‬
‫‪232‬‬
‫‪10‬‬
‫‪242-248‬‬
‫‪.28 ,23 ,20 ,14 ,11 ,8 ,3 ,5‬‬
‫‪243‬‬
‫‪.10 ,8 ,2 ,1‬‬