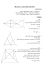עבודת קיץ לכיתה ח` - בית ספר לאומנויות

‫קיץ תשע"ב‬
‫עבודת קיץ במתמטיקה לבוגרי כיתה ח'‬
‫תלמידים יקרים‪,‬‬
‫כמידי סוף שנה אנו מציידים אתכם בעבודת קיץ במתמטיקה לחזרה וריענון בנושאים השונים שנלמדו‬
‫השנה‪.‬‬
‫בתחילת שנת הלימודים תשע"ג ייערך מבחן במתמטיקה שייכלול את הנושאים המופיעים בעבודה זו‪:‬‬
‫ יחס‪ ,‬פרופורציה וקנה מידה‬‫ פונקציה קוית‬‫ דימיון משולשים‬‫ משוואות‪ ,‬אי שיוויונות ובעיות מילוליות‬‫ אחוזים‬‫ סטטיסטיקה והסתברות‬‫ משפט פיתגורס‬‫ מערכת של שתי משוואות בשני נעלמים‬‫ טכניקה אלגברית (חוק הפילוג המורחב)‬‫ גיאומטריה (חפיפת משולשים‪ ,‬ישרים מקבילים‪ ,‬משולש שווה שוקיים‪ ,‬משולש ישר זוית‪,‬‬‫שטחים והיקפים)‬
‫אנו מקווים שתדעו לנצל את החופשה היטב‪ ,‬תהנו ‪ ,‬תנוחו ותאזרו כוחות לקראת השנה הבאה‪.‬‬
‫בברכת חופשה נעימה‪,‬‬
‫צוות המתמטיקה‬
‫‪1‬‬
‫יחס‪ ,‬פרופורציה וקנה מידה‬
‫‪ .1‬במבחן במתמטיקה שנערך בכיתות ח'‪ 1‬ו‪ -‬ח'‪ ,2‬היחס בין מספר הנכשלים לבין מספר העוברים‬
‫הוא ‪ 2:2‬בכל אחת מהכיתות‪.‬‬
‫א‪ .‬ידוע כי ‪ 8‬תלמידים בכיתה ח'‪ 1‬נכשלו במבחן‪ .‬כמה תלמידים עברו את המבחן?‬
‫ב‪ .‬כמה התלמידים לומדים בכיתה ח'‪?1‬‬
‫ג‪ .‬בכיתה ח'‪ 2‬עברו את המבחן ‪ 21‬תלמידים‪ .‬כמה תלמידים נכשלו?‬
‫ד‪ .‬כמה תלמידים לומדים בכיתה ח'‪?2‬‬
‫ה‪ .‬האם ייתכן שבכיתה ח'‪ 1‬נכשלו ‪ 9‬תלמידים? נמק‪.‬‬
‫‪ .2‬בכיתה י"א ובכיתה י"ב יש תלמידים המתנדבים במגן דוד אדום‪.‬‬
‫בכיתה י"א היחס בין מספר התלממידים המתנדבים במד"א לבין מספר התלמידים‬
‫שאינם מתנדבים הוא ‪.1:1‬‬
‫בכיתה י"ב היחס בין מספר התלממידים המתנדבים במד"א לבין מספר התלמידים‬
‫שאינם מתנדבים הוא ‪.1:1‬‬
‫בכל אחת מהכיתות ‪ 1‬תלמידים מתנדבים במגן דוד אדום‪.‬‬
‫א‪ .‬כמה תלמידים יש בסך הכל בכל כיתה? נמקו את תשובתכם במילים או בעזרת תרגיל‪.‬‬
‫ב‪ .‬בוחרים באופן אקראי תלמיד אחד מכלל התלמידים שבשתי הכיתות‪.‬‬
‫מהי ההסתברות שתלמיד זה מתנדב במד"א?‬
‫‪ .3‬ידוע כי‬
‫היחס בין הזוויות ‪  , ‬ו‪  -‬הוא ‪.2:3:2‬‬
‫מצא את גודלה של כל זווית‪.‬‬
‫‪ .2‬חילקו ‪ 31‬קלפי משחק בין דרור ועידו ביחס של ‪.2:1‬‬
‫אילו מההיגדים הבאים מתאים לתיאור החלוקה?‬
‫א‪ .‬על כל ‪ 2‬קלפים שקיבל דרור‪ ,‬עידו קיבל ‪ 1‬קלפים‪.‬‬
‫‪5‬‬
‫ב‪ .‬לעידו יש‬
‫‪7‬‬
‫מכלל הקלפים שחולקו‪.‬‬
‫ג‪ .‬מכל ‪ 2‬קלפים‪ ,‬עידו קיבל ‪ 2‬קלפים ודרור קיבל ‪ 1‬קלפים‪.‬‬
‫ד‪ .‬היחס בין מספר הקלפים שדרור קיבל לבין מספר הקלפים שעידו קיבל הוא ‪.1:11‬‬
‫ה‪ .‬היחס בין מספר הקלפים שעידו קיבל לבין מספר הקלפים הכולל הוא ‪.1:2‬‬
‫‪2‬‬
‫‪ .1‬אייל וארז קנו ביחד חבילה אחת של סוכריות‪.‬‬
‫אייל שילם ‪ 11‬ש"ח וארז שילם ‪ 21‬ש"ח‪.‬‬
‫א‪ .‬מה היחס בין הסכום ששילם אייל לבין הסכום ששילם ארז?‬
‫ב‪ .‬בחבילה היו ‪ 28‬סוכריות והן חולקו בהתאם ליחס בין הסכומים ששילמו אייל וארז‪.‬‬
‫כמה סוכריות קיבל כל אחד מהם?‬
‫‪ .1‬היקף מלבן הוא ‪ 12‬ס"מ‪ .‬היחס בין צלעותיו הוא ‪ .3:1‬מהם אורכי צלעות המלבן?‬
‫‪ .2‬בכל סעיף נתונה פרופורציה‪ .‬חשב את ערכו של ‪.x‬‬
‫‪70 x‬‬
‫א‪.‬‬
‫‪‬‬
‫‪98 21‬‬
‫‪x2 x3‬‬
‫ג‪.‬‬
‫‪‬‬
‫‪6‬‬
‫‪9‬‬
‫‪25 125‬‬
‫ב‪.‬‬
‫‪‬‬
‫‪x‬‬
‫‪30‬‬
‫‪ .8‬נתון משולש ישר זווית שאורכי ניצביו הם ‪ 2‬ס"מ ו‪ 11 -‬ס"מ‪.‬‬
‫הקטינו את אורכי הניצבים בצורה פרופורציונלית‪,‬‬
‫וקיבלו משולש ישר זווית‪ ,‬שאחד מניצביו הוא‬
‫‪ 2‬ס"מ‬
‫‪ 3.1‬ס"מ‬
‫‪ 3.1‬ס"מ (ראה שרטוט)‪ .‬חשבו את היקף המשולש החדש‪.‬‬
‫‪ 11‬ס"מ‬
‫‪ .9‬לפניך תרשים של דירה (‪.)ABCD‬‬
‫התרשים משורטט בקנה מידה של ‪.1:211‬‬
‫א‪ .‬מהן מידותיו של חדר המגורים במציאות?‬
‫ב‪ .‬מהו שטח חדר המגורים במציאות?‬
‫ג‪ .‬מהו שטח הדירה במציאות?‬
‫ד‪ .‬מהו היחס בין שטח חדר המגורים לשטח הדירה כולה?‬
‫ה‪ .‬מהו אורך הטפט לו ההורים זקוקים‪ ,‬אם הם רוצים לתלות אותו מסביב לכל חדר המשחקים?‬
‫אחוזים‬
‫‪ .1‬חברה לייבוא מכוניות ייבאה מחו"ל ‪ 811‬כלי רכב‪ 12.1% .‬הן מכוניות מנהלים‪ 22.1% ,‬הן‬
‫מכוניות משפחתיות‪ 11% ,‬הן משאיות‪ ,‬והשאר אופנועים‪ .‬כמה רכבים מכל סוג ייבאה החברה?‬
‫‪ .2‬בשקית יש סוכריות חמוצות וסוכריות מתוקות‪ 21% .‬מהסוכריות בשקית הן מתוקות‪ .‬מהו מספר‬
‫הסוכריות החמוצות‪ ,‬אם ידוע שמספר הסוכריות המתוקות הוא ‪?18‬‬
‫‪3‬‬
‫‪ .3‬במפעל גדול מועסקות ‪ 11‬נשים‪ .‬הנשים מהוות ‪ 31%‬מכלל עובדי המפעל‪.‬‬
‫א‪ .‬כמה עובדים יש במפעל?‬
‫ב‪ .‬כמה גברים מועסקים במפכל?‬
‫ג‪ .‬מהו היחס בין מספר הגברים למספר הנשים במפעל?‬
‫‪ .2‬נתון מלבן שאורכי צלעותיו הם ‪ 2‬ס"מ ו‪ 8 -‬ס"מ‪ .‬הגדילו את שתי הצלעות הנגדיות הקצרות של‬
‫המלבן ב‪ ,11% -‬והקטינו את שתי הצלעות הנגדיות הקצרות של המלבן ב‪.11% -‬‬
‫א‪ .‬חשב את השטח וההיקף של המלבן המקורי‪.‬‬
‫ב‪ .‬חשב את שטח וההיקף של המלבן החדש‪.‬‬
‫ג‪ .‬בכמה אחוזים קטן שטח המלבן החדש משטח המלבן המקורי?‬
‫פונקציה קוית‬
‫‪ .1‬א‪ .‬התאם כל פונקציה קווית לגרף המתאים לה משמאל‪:‬‬
‫‪1‬‬
‫‪x )i‬‬
‫‪4‬‬
‫‪y‬‬
‫‪y  2 x )ii‬‬
‫‪1‬‬
‫‪y   x )iii‬‬
‫‪2‬‬
‫‪y   x )iiii‬‬
‫ב‪ .‬רשום פונקציה קוית שתתאים לגרף המקוקו‪ .‬הסבר‪.‬‬
‫האם הפונקציה שרשמת היא פונקציה עולה או פונקציה יורדת?‬
‫‪1‬‬
‫‪ .2‬אחד הישרים שבשרטוט הוא גרף הפונקציה ‪. y   x  2‬‬
‫‪2‬‬
‫הישר השני הוא הישר המקביל לו‪.‬‬
‫א‪ .‬מי מבין הגרפים (‪ )I‬או (‪ )II‬מתאים לפונקציה הנתונה? הסבר‪.‬‬
‫ב‪ .‬מי מבין המשוואות הבאות יכולה להתאים לישר השני? נמק‪.‬‬
‫‪1‬‬
‫‪y  2 x  3 , y   x  1.5‬‬
‫‪2‬‬
‫‪1‬‬
‫‪1‬‬
‫‪y   x  3 , y  x  1.5 ,‬‬
‫‪2‬‬
‫‪2‬‬
‫‪I‬‬
‫‪II‬‬
‫‪y  2x  2 ,‬‬
‫ג‪ .‬רשום משוואת ישר המקביל לשני הגרפים שבשרטוט ועובר דרך ראשית הצירים‪.‬‬
‫‪ .3‬מצא את משוואת הישר ששיפועו ‪ 1‬ועובר דרך נקודת החיתוך של הישר ‪ y  4 x  10‬עם ציר ‪.y‬‬
‫‪ .2‬א‪ .‬מצא את משוואת הישר ששיפועו ‪ -3‬ועובר דרך הנקודה (‪.)-3 ; 8‬‬
‫ב‪ .‬אילו מבין הנקודות הבאות נמצאות על הישר מסעיף (א)‪)-1 ; 2(, )-2 ; 1( ,)-2 ; 1(, )1 ; -2( :‬‬
‫‪4‬‬
‫‪ .1‬א‪ .‬חשב את משוואת הישר העובר דרך הנקודות (‪ )1 ; 2‬ו‪.)-1 ; 13( -‬‬
‫ב‪ .‬חשב את משוואת הישר המקביל לישר מסעיף (א) ועובר דרך הנקודה (‪.)2 ; -2‬‬
‫ג‪ .‬מצא נקודה נוספת הנמצאת על הישר מסעיף (ב)‪.‬‬
‫‪2‬‬
‫‪ .1‬נתונות הפונקציות הבאות‪g ( x)  2 x  8 :‬‬
‫‪3‬‬
‫‪,‬‬
‫‪2‬‬
‫‪f ( x)   x  4‬‬
‫‪3‬‬
‫א‪ .‬התאם לכל פונקציה את הגרף שלה‪.‬‬
‫ב‪ .‬מצא את שיעורי הנקודות ‪ C ,B ,A‬ו‪.D -‬‬
‫ג‪ .‬הראה כי ‪. S1  S 2‬‬
‫ד‪ .‬חשב את משוואת הישר ‪.BD‬‬
‫ה‪ .‬האם הישר ‪ AC‬מקביל לישר ‪ ?BD‬נמק‪.‬‬
‫‪.2‬‬
‫ו‪ .‬מהו התחום עבורו )‪? g ( x)  f ( x‬‬
‫‪ .8‬חברת טלויזיה מציעה שני מסלולי תשלום עבור שירותי הטלויזיה שלה‪.‬‬
‫התשלום מורכב מדמי מנוי חודשיים ומתשלום עבור משך הצפייה בערוצי החברה‪.‬‬
‫לפניכם משוואות שני המסלולים‪ :‬מסלול ‪y  5x  120 :I‬‬
‫מסלול ‪y  10 x  100 :II‬‬
‫(‪ x‬מייצג את זמן הצפייה בשעות)‬
‫א‪ .‬מה מייצגים על פי הסיפור המספרים ‪ 11 ,121 ,1‬ו‪ 111 -‬בכל אחד מהמסלולים?‬
‫ב‪ .‬התאם בין כל מסלול לגרף המתאים לו בשרטוט‪ .‬נמק‪.‬‬
‫ג‪ .‬דני אומר כי בשני המסלולים משפחתו תשלם את אותו הסכום‪.‬‬
‫כמה שעות צופה משפחתו של דני בטלויזיה?‬
‫ד‪ .‬באיזה מסלול כדאי למשפחה הצופה בטלויזיה במשך ‪ 2‬שעות לבחור?‬
‫‪5‬‬
‫משוואות‪ ,‬אי שיוויונות ושאלות מילוליות‬
‫‪ .1‬פתור את המשוואות הבאות‪ ,‬רשום קבוצת הצבה במשוואות המתאימות ובדוק את תשובתך‪.‬‬
‫‪5 x  6 3x  6‬‬
‫‪‬‬
‫א‪ 0 .‬‬
‫‪4‬‬
‫‪2‬‬
‫‪6 3 4 1‬‬
‫ג‪.‬‬
‫‪  ‬‬
‫‪x 4 x 12‬‬
‫‪3x  6‬‬
‫ה‪ 3 .‬‬
‫‪x2‬‬
‫‪3x  1 11x  1 5 x  11‬‬
‫ב‪.‬‬
‫‪‬‬
‫‪‬‬
‫‪2‬‬
‫‪4‬‬
‫‪3‬‬
‫‪20 25‬‬
‫ד‪.‬‬
‫‪‬‬
‫‪x 1 x‬‬
‫‪4x 1‬‬
‫‪7‬‬
‫ו‪.‬‬
‫‪5 ‬‬
‫‪x2‬‬
‫‪x2‬‬
‫‪ .2‬פתור את אי השיוויונות הבאים‪ ,‬שרטט את הפיתרון על ציר המספרים‪.‬‬
‫א‪ 33x  1  7 x  5 .‬‬
‫ב‪ 35  x   4 x  3  47 .‬‬
‫‪2x  9‬‬
‫ג‪ 5 .‬‬
‫‪5‬‬
‫‪x  3 4 x  12‬‬
‫‪‬‬
‫ד‪ 0 .‬‬
‫‪2‬‬
‫‪8‬‬
‫‪ .3‬בית ספר הזמין ‪ 11‬אוטובוסים לטיול של שכבת ח'‪ .‬התכנון היה שבכל אוטובוס יהיה מספר שווה‬
‫של תלמידים‪ .‬בפועל הגיעו לבית הספר רק ‪ 2‬אוטובוסים‪ ,‬ולכן בכל אוטובוס נכנסו ‪ 12‬תלמידים‬
‫יותר מהתכנון המקורי‪.‬‬
‫א‪ .‬כמה תלמידים יצאו לטיול?‬
‫ב‪ .‬כמה תלמידים היו אמורים לנסוע בכל אטובוס (לפי התכנון המקורי)‪ ,‬וכמה תלמידים נסעו‬
‫בפועל בכל אוטובוס?‬
‫‪ .2‬בעל חנות גלידה קנה סוכריות צבעוניות ופתיתי שוקולד לקישוט כדורי הגלידה שנמכרים בחנותו‪.‬‬
‫בסך הכל קנה ‪ 8‬ק"ג‪ .‬מחיר ק"ג אחד של סוכריות צבעוניות הוא ‪ 21‬ש"ח‪ ,‬ומחיר ק"ג אחד של‬
‫פתיתי שוקולד הוא ‪ 31‬ש"ח‪ .‬בסה"כ שילם בעל החנות עבור הקנייה ‪ 221‬ש"ח‪.‬‬
‫כמה ק"ג סוכריות צבעוניות וכמה ק"ג פתיתי שוקולד קנה בעל חנות הגלידה?‬
‫‪ .1‬מונית ומשאית יצאו באותו הזמן מעיר א' לעיר ב'‪ .‬מהירות המשאית הייתה ‪ 11‬קמ"ש‪ ,‬ומהירות‬
‫המונית הייתה ‪ 21‬קמ"ש‪ .‬המשאית הגיעה לעיר ב' ‪ 3‬שעות אחרי המונית‪.‬‬
‫חשב את זמן הנסיעה של כל אחד מהרכבים ואת המרחק בין הערים‪.‬‬
‫‪ .1‬משני מקומות שהמרחק בינהם הוא ‪ 211‬ק"מ יצאו זה לקראת זה שני רוכבי אופניים‪.‬‬
‫הראשון יצא בשעה ‪ 2:11‬בבוקר‪ ,‬והשני יצא בשעה ‪ 8:11‬בבוקר‪ .‬הם נפגשו בשעה ‪12:11‬‬
‫בצהריים‪ .‬מהירות רוכב האופניים שיצא בשעה ‪ 2:11‬בבוקר הייתה קטנה ב‪ 1 -‬קמ"ש ממהירות‬
‫רוכב האופניים השני‪ .‬מהי מהירותו של כל רוכב? וכמה ק"מ עבר כל רוכב עד הפגישה?‬
‫‪ .2‬הגובה ‪ KM‬במשולש ‪ KLN‬מקצה על הקטע ‪ LN‬שני קטעים‪.‬‬
‫אורך הקטע האחד הוא ‪ 2‬ס"מ‪ ,‬ואורך הקטע השני הוא ‪ 3‬ס"מ‪.‬‬
‫שטח המשולש ‪ KLM‬גדול ב‪ 12 -‬סמ"ר משטח משולש ‪. KMN‬‬
‫מצא את אורך הגובה ‪.KM‬‬
‫‪6‬‬
‫מערכת של שתי משוואות בשני נעלמים‬
‫‪ .1‬פתור את מערכות המשוואות הבאות בשיטה הנוחה לך (הצבה ‪ /‬השוואת מקדמים)‪.‬‬
‫ב‪.‬‬
‫א‪.‬‬
‫‪x  y  7‬‬
‫‪‬‬
‫‪ x  y  1‬‬
‫ד‪.‬‬
‫ג‪.‬‬
‫‪2 x  y  7‬‬
‫‪‬‬
‫‪7 x  2 y  19‬‬
‫‪ 2 x  y  5‬‬
‫‪‬‬
‫‪2 x  7 y  19‬‬
‫‪5 x  8 y  4‬‬
‫‪‬‬
‫‪ x  7 y  18‬‬
‫‪ .2‬פתור את מערכות המשוואות הבאות‪:‬‬
‫א‪.‬‬
‫ב‪.‬‬
‫‪ 2x  y 9 y  2‬‬
‫‪‬‬
‫‪‬‬
‫‪5‬‬
‫‪ 3‬‬
‫‪5 x  4 y  33‬‬
‫ג‪.‬‬
‫‪ 2x y‬‬
‫‪ 3  2  5‬‬
‫‪‬‬
‫‪5x  3 y  4‬‬
‫‪ 3‬‬
‫‪2‬‬
‫‪7  2x y  8‬‬
‫‪ 5  10  2‬‬
‫‪‬‬
‫‪ x 1  4  5y  2‬‬
‫‪ 3‬‬
‫‪2‬‬
‫‪ .3‬מחירם של ‪ 2‬ק"ג אפרסקים ו‪ 3 -‬ק"ג ענבים הוא ‪ 21‬ש"ח‪.‬‬
‫המחיר של ‪ 1‬ק"ג אפרסקים גבוה ב‪ 1 -‬ש"ח מהמחיר של ‪ 2‬ק"ג ענבים‪.‬‬
‫א‪ .‬סמנו ב‪ x -‬את מחיר ק"ג האפרסקים וב‪ y -‬את מחיר ק"ג הענבים‪ ,‬ורשמו מערכת משוואות‬
‫המתאימה לבעיה זו‪.‬‬
‫ב‪ .‬מהו המחיר של ק"ג אפרסקים? ומהו המחיר של ק"ג ענבים?‬
‫‪ .2‬במשולש שווה שוקיים‪ ,‬אורך השוק ‪ x‬ס"מ ואורך הבסיס ‪ y‬ס"מ‪ .‬היקפו ‪ 13‬ס"מ‪.‬‬
‫אם נגדיל את השוק ב‪ 3 -‬ס"מ ונקטין את הבסיס ב‪ 2 -‬ס"מ‪ ,‬נקבל משולש שווה‬
‫שוקיים חדש שהיקפו גדול ב‪ 2 -‬ס"מ מהיקף המשולש הנתון‪.‬‬
‫א‪ .‬רשום מערכת משוואות המתאימה לתיאור השאלה‪.‬‬
‫ב‪ .‬מהן מידותיו של המשולש הנתון?‬
‫‪ .1‬התאם בין הייצוג האלגברי לייצוג הגרפי והסבר‪:‬‬
‫‪6 x  9 y  12‬‬
‫א‪.‬‬
‫‪‬‬
‫‪2 x  3 y  4‬‬
‫‪6 x  9 y  4‬‬
‫ב‪.‬‬
‫‪‬‬
‫‪2 x  3 y  12‬‬
‫‪7‬‬
‫‪9 x  3 y  12‬‬
‫ג‪.‬‬
‫‪‬‬
‫‪ 3 x  2 y  8‬‬
‫‪.1‬‬
‫טכניקה אלגברית‬
‫‪ .1‬השלם את החסר בכל אחד מהמקומות הריקים (השתמש בחוק הפילוג המורחב)‪:‬‬
‫א‪.‬‬
‫‪x  2x  ____   _____  3x  _____  6‬‬
‫ב‪.‬‬
‫‪ y  10 y  ____   y 2  _____  _____  50‬‬
‫ג‪.‬‬
‫‪2b  4b  ____   2b 2  _____  _____  28‬‬
‫ד‪.‬‬
‫_____ ‪ ____  1 ____  4  c 2  4c  _____ ‬‬
‫ה‪.‬‬
‫_____ ‪ ____  6x  ____   x 2  7 x  _____ ‬‬
‫‪.2‬‬
‫‪ .3‬נתון ריבוע שאורך צלעו ‪ x‬ס"מ‪.‬‬
‫האריכו את צלעות הריבוע כמתואר בשרטוט וקיבלו מלבן‪.‬‬
‫ידוע כי שטח המלבן שהתקבל גדול ב‪ 22 -‬סמ"ר משטח הריבוע‪.‬‬
‫א‪ .‬רשום משוואה מתאימה ומצא את אורך צלע הריבוע‪.‬‬
‫ב‪ .‬חשב את היקף המלבן‪.‬‬
‫‪8‬‬
‫‪ .2‬היקפו של המלבן משמאל הוא ‪ 11‬ס"מ‪.‬‬
‫אם מגדילים את הצלע האחת שלו ב‪ 3 -‬ס"מ ואת הצלע השנייה ב‪ 2 -‬ס"מ‪,‬‬
‫מקבלים מלבן חדש ששטחו גדול ב‪ 21 -‬סמ"ר משטח המלבן המקורי‪.‬‬
‫חשב את צלעות המלבן המקורי‪.‬‬
‫סטטיסטיקה והסתברות‬
‫‪ .1‬ציוניה של גלית בלשון בשליש א' הם‪.21 ,13 , 98 :‬‬
‫בשליש ב' התקיימו ‪ 2‬מבחנים וציוניה של גלית היו‪.22 ,11 :‬‬
‫מהו הציון שצריכה גלית לקבל במבחן השלישי בלשון‪ ,‬כדי שממוצע הציונים שלה בשליש ב' יהיה‬
‫זהה לממוצע הציונים שלה בשליש א'? הסבר‪.‬‬
‫‪ .2‬לפניך הציונים במתמטיקה שקיבלו בתעודה תלמידי כיתה ח'‪:‬‬
‫‪.21 ,21 ,21 ,11 ,21 ,21 ,11 ,91 ,81 ,81 ,11 ,91 ,81 ,81 ,111‬‬
‫א‪ .‬השלם את הטבלה הבאה‪:‬‬
‫ציון‬
‫‪11‬‬
‫‪21‬‬
‫‪11‬‬
‫‪81‬‬
‫שכיחות‬
‫שכיחות יחסית‬
‫ב‪ .‬כמה תלמידים בכיתה?‬
‫ג‪ .‬מהו ממוצע הציונים בכיתה?‬
‫ד‪ .‬מהו הציון החציוני של התלמידים בכיתה?‬
‫ה‪ .‬מהו הציון השכיח של תלמידי הכיתה?‬
‫ו‪ .‬כמה תלמידים קיבלו ציון מעל ‪?81‬‬
‫ז‪ .‬מהי השכיחות היחסית של התלמידים שקיבלו ציון גבוה מ‪?81 -‬‬
‫ח‪ .‬מהו אחוז התלמידים שקיבלו ציון עובר (‪ 11‬ומעלה)?‬
‫ט‪ .‬מהי ההסתברות שתלמיד שנבחר באקראי קיבל את הציון ‪?21‬‬
‫י‪ .‬שרטט דיאגרמת עמודות מתאימה‪.‬‬
‫‪ .3‬במסיבה נמכרו ‪ 311‬כרטיסי הגרלה‪ .‬הפרסים שחולקו בהגרלה הם‪:‬‬
‫‪ 1‬אופניים‪ 3 ,‬מערכות סטריאו‪ 12 ,‬משחקי מחשב‪ ,‬ו‪ 31 -‬תקליטורי מוזיקה‪.‬‬
‫א‪ .‬מה ההסתברות לזכות במערכת סטריאו?‬
‫ב‪ .‬מה ההסתברות לזכות בתקליטור מוזיקה?‬
‫ג‪ .‬מה ההסתברות לזכות בפרס כלשהו?‬
‫ד‪ .‬מה ההסתברות לא לזכות כלל בפרס?‬
‫‪9‬‬
‫‪91‬‬
‫‪111‬‬
‫‪.2‬‬
‫‪.1‬‬
‫הצבות‬
‫‪ .1‬נתונה הפונקציה ‪y = x2 - 2x +1 :‬‬
‫מה ערך של ‪ y‬אם נתון ‪x = -1 , x = 0 , x = 5 :‬‬
‫‪ .2‬נתונה הפונקציה ‪y = - x2 - 2x +1 :‬‬
‫מה ערך של ‪ y‬אם נתון ‪x = -2 , x = -1 , x = 0 :‬‬
‫‪ .3‬נתונה הפונקציה ‪y = -2x2 - 4x +4 :‬‬
‫מה ערך של ‪ y‬אם נתון ‪x = -3 , x = -3 , x = 5 :‬‬
‫‪11‬‬
‫הצבות – תזכורת‪:‬‬
‫‪2‬‬
‫‪ , x‬הציבו ‪x = -2‬‬
‫‪2‬‬
‫‪(-2) = 4‬‬
‫הצבה של מספר שלילי תמיד בתוך סוגריים‬
‫‪2‬‬
‫‪x = -2‬‬
‫‪ , - x‬הציבו ‪x = 2‬‬
‫‪2‬‬
‫‪2‬‬
‫‪-( -2 ) = -4‬‬
‫‪-2 = - 4‬‬
‫משפט פיתגורס‬
‫‪ .1‬נתון‪ . ABC ~ DEF :‬יחס הדימיון הוא ‪.2‬‬
‫א‪ .‬חשב את ‪.BC‬‬
‫ב‪ .‬חשב את אורכי צלעות ‪. DEF‬‬
‫ג‪ .‬חשב את שטח ‪. ABC‬‬
‫ד‪ .‬ניתן למצוא את שטח ‪ DEF‬בשתי דרכים‪ .‬מהן שתי הדרכים?‬
‫‪ .2‬בשרטוט משמאל נתונים מלבן ‪ CBED‬ומשולש ‪.BEA‬‬
‫נתון כי‪ 9 :‬ס"מ = ‪ 21 ,AE‬ס"מ = ‪ 39 ,AB‬ס"מ = ‪.AD‬‬
‫א‪ .‬חשב את אורך צלע ‪.BE‬‬
‫ב‪ .‬חשב את אורך צלע ‪.BC‬‬
‫ג‪ .‬חשב את היקף מרובע ‪.ABCD‬‬
‫ד‪ .‬חשב את אורך אלכסון ‪ CE‬במלבן ‪.BCDE‬‬
‫‪ .3‬לכבוד יום העצמאות צייר רותם דגל שמידותיו בס"מ נתונות בציור משמאל‪.‬‬
‫נתון‪EF = BC :‬‬
‫א‪ .‬חשב את שטחו של הדגל‪ .‬הסבר‪.‬‬
‫ב‪ .‬חשב את היקף הדגל (היקף ‪ .)BCDEF‬הסבר‪.‬‬
‫דימיון משולשים‬
‫‪ .1‬לפניך שני משולשים‪.‬‬
‫א‪ .‬האם המשולשים דומים?‬
‫אם לא – נמק‬
‫אם כן – השלם‪:‬‬
‫ב‪ .‬מהו יחס הדימיון?‬
‫ג‪ .‬ידוע כי ‪ .FE=12‬חשב את הצלע המתאימה לה במשולש ‪. ABC‬‬
‫ד‪ .‬ידוע ששטח ‪ ABC‬הוא ‪ 192‬סמ"ר‪ .‬מהו שטח ‪ ? DEF‬הסבר חישוביך‪.‬‬
‫‪ .2‬בשרטוט שלפניך נתון כי ‪DE‬‬
‫‪. AB‬‬
‫א‪ .‬הסבר מדוע המשולשים שבשרטוט דומים וכתוב את הדימיון בכתיב אלגברי‪.‬‬
‫ב‪ .‬מהו יחס הדימיון בין המשולש הקטן למשולש הגדול?‬
‫ג‪ .‬חשב על פי הנתונים שבשרטוט את אורכי הצלעות ‪ DE‬ו‪.CE -‬‬
‫ד‪ .‬מהו יחס השטחים בין המשולש הקטן למשולש הגדול?‬
‫ה‪ .‬מהו יחס ההיקפים בין המשולש הקטן למשולש הגדול?‬
‫‪11‬‬
‫גיאמטריה (חפיפת משולשים‪ ,‬ישרים מקבילים‪ ,‬משולש שווה שוקיים משולש ישר זוית)‬
‫‪ .1‬בדוק בכל סעיף האם המשולשים חופפים‪.‬‬
‫אם הם חופפים‪ ,‬רשום לפי איזה משפט חפיפה‪ .‬אם אינם חופפים‪ ,‬הסבר מדוע‪.‬‬
‫‪.2‬‬
‫‪.3‬‬
‫‪.2‬‬
‫‪12‬‬
‫‪.1‬‬
‫‪.1‬‬
‫‪ .2‬משולש ‪ ABC‬הוא שווה שוקיים (‪)AB = AC‬‬
‫הנקודה ‪ D‬נמצאת על המשך הצלע ‪.AB‬‬
‫הנקודה ‪ E‬נמצאת על המשך הצלע ‪.AC‬‬
‫א‪ .‬הסבר מדוע‬
‫ב‪ .‬נתון גם‪BD = CE :‬‬
‫הנקודה ‪ F‬היא אמצע ‪BC‬‬
‫הוכח כי ‪BDF  CEF‬‬
‫(פרט את החפיפה ואת משפט החפיפה בו השתמשת)‬
‫‪13‬‬
‫‪.8‬‬
‫‪.9‬‬
‫פתרו בשתי דרכים שונות‬
‫‪.11‬‬
‫‪14‬‬