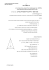מבחן לדוגמא + פתרונות סופיים

‫ארכימדס ‪ -‬פתרונות למידה‬
‫הכנה לבחינת הבגרות בשאלון ‪806‬‬
‫שאלון ‪ - 806‬מבחן ‪31‬‬
‫פרק ראשון ‪ -‬אלגברה והסתברות )‪ 40‬נק'(‬
‫ענה על שתיים מהשאלות ‪) 1-3‬לכל שאלה ‪ 20‬נק'(‬
‫‪ .1‬מנהל מפעל מעסיק מדי יום חמישה עובדים‪ ,‬חלקם ותיקים וחלקם חדשים‪ ,‬באריזת מכסה יומית קבועה‬
‫של מוצרים‪ .‬מספר העובדים החדשים משתנה מדי יום‪ .‬פועל ותיק מסוגל לסיים לבדו את המכסה‬
‫היומית בזמן הקצר פי שניים מהדרוש לפועל חדש‪ .‬ביום א' סיים הצוות המשולב לארוז ‪ 75%‬מהמכסה‬
‫היומית בתוך שעתיים‪ .‬ביום ב'‪ ,‬מספר העובדים החדשים בצוות היה גדול פי שניים ממספר העובדים‬
‫החדשים ביום א'‪ .‬ביום ב'‪ ,‬בתום שעתיים של עבודה‪ ,‬סיים הצוות לארוז ‪ 2‬מהמכסה היומית‪.‬‬
‫‪3‬‬
‫א‪ .‬מצא כמה עובדים חדשים עבדו ביום ב'‪.‬‬
‫ב‪ .‬נתון‪ :‬פועל ותיק אורז עשרים חבילות בשעה‪ .‬חשב כמה זמן לקח לצוות ביום א' לארוז ‪ 135‬מתנות‪.‬‬
‫‪ .2‬בסדרה הנדסית עולה שאיבריה חיוביים‪ ,‬האיבר הראשון ‪ a1‬והמנה ‪ . q‬אם נפחית ‪ 2‬מהאיבר הראשון‬
‫ונכפיל פי שניים את האיבר השלישי‪ ,‬יהיו שלושת האיברים הראשונים סדרה הנדסית חדשה בפני עצמה‪.‬‬
‫א‪ .‬מצא את האיבר הראשון בסדרה החדשה‪.‬‬
‫ב‪ .‬ממשיכים את הסדרה החדשה כך שיהיה בה מספר זוגי של איברים‪ .‬סכום הסדרה החדשה גדול‬
‫יותר מפי ‪ 1.25‬מסכום איבריה הנמצאים במקומות הזוגיים‪ .‬מצא את התחום האפשרי של ערכי ‪. q‬‬
‫‪ .3‬חלק מעובדי התאגיד יצאו לפני שבוע לקורס ניהולי והיתר לא‪ .‬ההסתברות לבחור מבין כלל העובדים‬
‫ארבעה עובדים )גברים או נשים( שיצאו לקורס היא ‪ .0.0016‬רבע מהעובדים שלא יצאו לקורס הן נשים‪.‬‬
‫מבין כלל העובדים‪ ,‬שיעור כלל הגברים גדול פי ‪ 15‬משיעור הנשים שיצאו לקורס‪.‬‬
‫א‪ .‬מירב עובדת בתאגיד‪ .‬חשב את ההסתברות שיצאה לקורס ניהולי‪.‬‬
‫ב‪ .‬קבע האם האירועים‪' :‬לצאת לקורס' ו‪'-‬להיות גבר' הם תלויים או בלתי תלויים‪ .‬נמק‪.‬‬
‫ג‪ .‬כל מי שלא יצא לקורס‪ ,‬ניגש אתמול למבחן התאמה‪ ,‬שהצלחה בו תאפשר לצאת לקורס‪ .‬שישית‬
‫מהגברים שניגשו למבחן אתמול‪ ,‬עברו אותו בהצלחה‪ 75% .‬מכלל הניגשים למבחן נכשלו בו‪.‬‬
‫חשב את שיעור הנשים מבין אלו שעברו בהצלחה את המבחן‪.‬‬
‫פרק שני ‪ -‬גיאומטריה וטריגונומטריה במישור )‪ 20‬נק'(‬
‫ענה על אחת מהשאלות מהשאלות ‪ 20) 4-5‬נק'(‬
‫‪ .4‬הישר ‪ AE‬הוא תיכון במשולש ‪ . ∆ABC‬הנקודות ‪ D‬ו‪ F-‬נמצאות על‬
‫הצלע ‪ .AB‬הישרים ‪ CD‬ו‪ AE-‬נחתכים בנקודה ‪.O‬‬
‫נתון‪. AC = 1.5 BE , BE FO :‬‬
‫שטח המשולש ‪ ∆AFO‬הוא ‪ 9m‬ושטח המרובע ‪ BEOF‬הוא ‪. 16m‬‬
‫א‪ .‬הוכח‪. p ACD = p BCD :‬‬
‫ב‪ .‬הוכח‪. AC ⋅ BD = 2 :‬‬
‫‪AD ⋅ CE‬‬
‫© כל הזכויות שמורות לארכימדס ‪ -‬פתרונות למידה ‪ -‬הכנה לבחינת הבגרות בשאלון ‪806‬‬
‫עמוד ‪226‬‬
‫הכנה לבחינת הבגרות בשאלון ‪806‬‬
‫ארכימדס ‪ -‬פתרונות למידה‬
‫‪ .5‬א‪ .‬הוכח את הזהות‪. tan( −α ) = − tan(α ) :‬‬
‫ב‪ .‬המשולש ‪ ∆ABC‬חוסם מעגל המשיק לו בנקודות ‪ E ,D‬ו‪.F-‬‬
‫נתון‪. p ABC = 180 − 2 β , p ADE = α , DE = m :‬‬
‫הבע באמצעות ‪ β , α‬ו‪ m -‬את אורך המשיק ‪BF‬‬
‫) ‪m ⋅ tan (α + β‬‬
‫‪. CF = −‬‬
‫והוכח שמתקיים‪:‬‬
‫‪2 sin α‬‬
‫ג‪ .‬היעזר בסעיף א' והוכח שאם ‪ , CF = BF‬אז הנקודה ‪ F‬רחוקה במידה שווה מהנקודות ‪ D‬ו‪.E-‬‬
‫פרק שלישי ‪ -‬חשבון דיפרנציאלי ואינטגרלי של פולינומים‪ ,‬פונקציות שורש‪ ,‬פונקציות רציונליות‬
‫ופונקציות טריגונומטריות )‪ 40‬נק'(‬
‫ענה על שתיים מהשאלות ‪) 6-8‬לכל שאלה ‪ 20‬נק'(‬
‫‪ax 2 − 4‬‬
‫= ) ‪ . f ( x‬שתיים מהאסימפטוטות של‬
‫‪ .6‬הישר ‪ y = 1‬הוא אסימפטוטה אופקית של הפונקציה‪:‬‬
‫‪ax − b‬‬
‫גרף )‪ f (x‬ושני הצירים‪ ,‬יוצרים ברביע הראשון מלבן ששטחו ‪ 7‬יח"ר‪ .‬הפרמטרים ‪ a‬ו‪ b-‬חיוביים‪.‬‬
‫א‪ .‬עבור גרף הפונקציה )‪ f (x‬מצא את‪:‬‬
‫‪ .2‬נקודות הקיצון וסוגן‪ ,‬במידה וקיימות‪.‬‬
‫‪ .1‬ערכם של ‪ a‬ו‪ b-‬ותחום ההגדרה‪.‬‬
‫‪ .4‬תחומי העליה והירידה‪.‬‬
‫‪ .3‬נקודות החיתוך עם הצירים‪.‬‬
‫ב‪ .‬שרטט את גרף הפונקציה )‪. f (x‬‬
‫ג‪ .‬הגדירו פונקציה חדשה‪ . g ( x) = − f ( x) :‬נתון‪ :‬למשוואה ‪ g ( x ) = m‬יש פתרון יחיד‪.‬‬
‫מצא את ערכו של הפרמטר ‪.m‬‬
‫‪ .7‬נתון מספר בתחום‪ . 1 ≤ x ≤ 36 :‬באמצעותו מרכיבים שלושה מספרים נוספים‪:‬‬
‫המספר השני הוא השורש הריבועי של המספר הראשון‪ .‬המספר השלישי קטן ב‪ 1-‬מהמספר השני‪.‬‬
‫המספר הרביעי קטן ב‪ 4-‬מהמספר השני‪ .‬מעלים בריבוע את המספר הרביעי‪ ,‬ומכפילים את התוצאה‬
‫במספר השלישי‪.‬‬
‫א‪ .‬מצא את המספר הראשון‪ ,‬שעבורו מכפלה זו היא‪:‬‬
‫‪ .1‬מינימלית‪.‬‬
‫‪ .2‬מקסימלית‪.‬‬
‫ב‪ .‬חשב את ההפרש בין המכפלה המקסימלית האפשרית לבין המכפלה המינימלית האפשרית‪.‬‬
‫‪3π ‬‬
‫‪ .8‬נתונה הפונקציה‪ :‬‬
‫‪ x ‬‬
‫‪. f ( x) = sin ‬‬
‫א‪ .‬הוכח‪ :‬כל נקודות הקיצון של גרף הפונקציה )‪ f (x‬נמצאות במרחק של יח' אורך אחת מציר ה‪-‬‬
‫‪.x‬‬
‫ב‪ .‬את הסעיפים הבאים בצע בתחום ‪: 1 ≤ x ≤ 3‬‬
‫‪ .1‬מצא את נקודות החיתוך של גרף הפונקציה )‪ f (x‬עם ציר ה‪.x-‬‬
‫‪ .2‬מצא את נקודות הקיצון של גרף הפונקציה )‪ , f (x‬כולל בקצה התחום‪ ,‬ואת סוגן‪.‬‬
‫‪ .3‬שרטט את גרף הפונקציה )‪. f (x‬‬
‫ג‪ .‬נתון‪ . f ' ( x) = g ( x) :‬הפונקציה )‪ g (x‬חיובית לכל ‪ x‬בתחום ‪. 2 ≤ x ≤ 3‬‬
‫חשב את השטח הכלוא בין גרף הפונקציה )‪ g (x‬לבין ציר ה‪ x-‬והישרים ‪ x = 2‬ו‪. x = 3 :‬‬
‫בהצלחה!‬
‫© כל הזכויות שמורות לארכימדס ‪ -‬פתרונות למידה ‪ -‬הכנה לבחינת הבגרות בשאלון ‪806‬‬
‫עמוד ‪227‬‬
‫הכנה לבחינת הבגרות בשאלון ‪806‬‬
‫ארכימדס ‪ -‬פתרונות למידה‬
‫פתרונות‪:‬‬
‫‪ (1‬א‪ .‬שניים‪ .‬ב‪ .‬שעה וחצי‪.‬‬
‫‪ (2‬א‪ .2 .‬ב‪. 1 < q < 2 .‬‬
‫‪ (3‬א‪ .0.2 .‬ב‪ .‬בלתי תלויים‪ .‬ג‪.50% .‬‬
‫‪m ⋅ tan β‬‬
‫= ‪. BF‬‬
‫‪ (5‬ב‪.‬‬
‫‪2 sin α‬‬
‫‪ (6‬א‪. a = 1, b = 7 .1 .‬‬
‫תחום ההגדרה‪ 7 < x :‬או ‪ 2 ≤ x < 7‬או ‪. x ≤ −2‬‬
‫‪. (−2, 0), (2, 0) .3 . max (−2, 0), max (2, 0) .2‬‬
‫‪ .4‬עולה‪ ; x < −2 :‬יורדת‪ 7 < x :‬או ‪. 2 < x < 7‬‬
‫ב‪ .‬השרטוט משמאל‪ .‬ג‪. m = −1 .‬‬
‫‪ (7‬א‪ 1 (1 .‬או ‪ .36 (2 .16‬ב‪ .‬ההפרש ‪.20‬‬
‫‪ (8‬ב‪. min (1, 0), max (1.2,1), min (2, − 1), max (3, 0) (2 . (1, 0), (1.5, 0), (3, 0) (1 .‬‬
‫‪ (3‬השרטוט משמאל‪ .‬ג‪ 1 .‬יח"ר‪.‬‬
‫© כל הזכויות שמורות לארכימדס ‪ -‬פתרונות למידה ‪ -‬הכנה לבחינת הבגרות בשאלון ‪806‬‬
‫עמוד ‪228‬‬