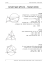מעגל ב פרופורציות

‫פרופורציות במעגל‬
‫משפט ‪ :‬שני מיתרים הנחתכים במעגל מחלקים זה את זה לשני‬
‫קטעים ‪ ,‬כך שמכפלת קטעי מיתר אחד שווה למכפלת קטעי המיתר‬
‫השני ‪.‬‬
‫‪B‬‬
‫במילים אחרות ‪ ,‬אם המיתרים‬
‫‪ AC‬ו‪ BD -‬נחתכים בנקודה ‪, E‬‬
‫‪C‬‬
‫‪A‬‬
‫‪E‬‬
‫אזי מתקיים ‪. AE  CE  BE  DE :‬‬
‫‪D‬‬
‫דוגמה ‪:‬‬
‫‪A‬‬
‫המיתרים ‪ AC‬ו‪ BD -‬נחתכים בנקודה ‪. E‬‬
‫‪B‬‬
‫נתון ‪ 4 :‬ס " מ ‪ 3 , BE ‬ס " מ ‪, DE ‬‬
‫‪E‬‬
‫‪. CE  3  AE‬‬
‫חשב את אורך המיתר ‪. AC‬‬
‫‪D‬‬
‫‪C‬‬
‫פתרון ‪:‬‬
‫‪ AC‬ו‪ BD -‬הם שני מיתרים במעגל הנחתכים בנקודה ‪ , E‬ולכן‬
‫‪ ) AE  CE  BE  DE‬לפי המשפט ‪ :‬אם שני מיתרים במעגל נחתכים ‪ ,‬אז‬
‫מכפלת קטעי המיתר האחד שווה למכפלת קטעי המיתר השני (‪.‬‬
‫על פי הנתון ‪ 4 :‬ס " מ ‪ 3 , BE ‬ס " מ ‪ . CE  3  AE , DE ‬נסמן ‪, AE  x :‬‬
‫ומכאן ‪ . CE  3x‬נציב ונקבל ‪ , x  3x  4  3 :‬כלומר ‪3x 2  12‬‬
‫‪2‬‬
‫ומכאן ‪ . x  4‬פתרונות המשוואה הם ‪ x  2‬א ו ‪. x  2‬‬
‫הפתרון ‪ x  2‬נפסל ‪ ,‬מכיוון ש‪ x -‬מייצג אורך של קטע ולכן אינו יכול‬
‫לקבל ערך שלילי ‪.‬‬
‫נציב את הפתרון ‪ x  2‬ונקבל ‪ 2 :‬ס " מ ‪ 6 , AE  x ‬ס " מ ‪. CE  3x  3  2 ‬‬
‫נחשב את ‪ 8 : AC‬ס " מ ‪. AC  AE  CE  2  6 ‬‬
‫משפט ‪ :‬אם מנקודה שמחוץ למעגל יוצאים למעגל שני חותכים ‪,‬‬
‫אז המכפלה של חותך אחד בחלק ו החיצוני שווה למכפלה של החותך‬
‫השני בחלקו החיצוני ‪.‬‬
‫בציור שלפניך ‪ ABC‬הוא חותך למעגל‬
‫) כלומר ‪ AB‬הוא החלק החיצוני של החותך (‬
‫‪C‬‬
‫‪B‬‬
‫ו‪ ADE -‬הוא חותך למעגל ) כלומר ‪AD‬‬
‫‪A‬‬
‫הוא החלק החיצוני של החותך (‬
‫ולכן מתקיים ‪. AC  AB  AE  AD :‬‬
‫‪119‬‬
‫‪D‬‬
‫‪E‬‬
‫דוגמה ‪:‬‬
‫‪C‬‬
‫‪ ABC‬ו‪ ADE -‬הם שני חותכים למעגל‬
‫‪B‬‬
‫שמרכזו ‪ . O‬נתון ‪ 8 :‬ס " מ ‪, AO ‬‬
‫‪ 6‬ס " מ ‪. AO  CO , CO ‬‬
‫‪E‬‬
‫‪A‬‬
‫‪D‬‬
‫‪O‬‬
‫חשב את אורך הקטע ‪. AB‬‬
‫פתרון ‪:‬‬
‫נתון ‪ AO  CO :‬ולכן המשולש ‪ AOC‬הוא משולש ישר‪ -‬זווית‬
‫שבו ‪ 8‬ס " מ ‪ 6 , AO ‬ס " מ ‪ . CO ‬נחשב את ‪. AC‬‬
‫לפי משפט פיתגורס ‪ ,‬במשולש ‪ AOC‬מתקיים ‪:‬‬
‫‪2‬‬
‫‪2‬‬
‫‪2‬‬
‫‪. AO  OC  AC‬‬
‫נציב ו נקבל ‪ , 82  62  AC2 :‬ומכאן ‪ 10 :‬ס " מ ‪. AC ‬‬
‫‪ ABC‬ו‪ ADE -‬הם שני חותכים למעגל ולכן מתקיים ‪AC  AB  AE  AD :‬‬
‫) לפי המשפט ‪ :‬אם מנקודה שמחוץ למעגל יוצאים למעגל שני חותכים ‪,‬‬
‫אז מכפלת חותך אחד בחלקו החיצוני שווה למכפלת החותך השני‬
‫בחלקו החיצוני (‪ .‬מצאנו כי ‪ 10‬ס " מ ‪ . AC ‬על פי הנתון ‪ 6 :‬ס " מ ‪, CO ‬‬
‫כלומר רדיוס המעגל הוא ‪ 6‬ס " מ ‪ ,‬ומכאן ‪ 6‬ס " מ ‪DO  OE ‬‬
‫) הרי במעגל כל הרדיוסים שווים (‪.‬‬
‫נחשב את ‪: AD‬‬
‫נחשב את ‪: AE‬‬
‫‪ 2‬ס " מ ‪AD  AO  DO  8  6 ‬‬
‫‪ 14‬ס " מ ‪AE  AO  OE  8  6 ‬‬
‫ראינו כי מתקיים ‪ . AC  AB  AE  AD :‬נציב ונקבל ‪10  AB  14  2 :‬‬
‫ומכאן ‪ 2.8‬ס " מ ‪. AB ‬‬
‫משפט ‪ :‬אם מנקודה שמחוץ למעגל יוצאים למעגל משיק וחותך ‪,‬‬
‫אז המכפלה של החותך בחלקו החיצוני שווה לריבוע המשיק ‪.‬‬
‫‪D‬‬
‫במילים אחרות ‪ ,‬אם ‪ ABC‬הוא חותך‬
‫למעגל ) כלומר ‪ AB‬הוא החלק החיצוני‬
‫‪A‬‬
‫של החותך ( ו‪ AD -‬הוא משיק למעגל ‪,‬‬
‫‪B‬‬
‫אזי מתקיים ‪. AC  AB  AD 2 :‬‬
‫‪C‬‬
‫דוגמה ‪:‬‬
‫‪ EF‬הוא קוטר במעגל שמרכזו ‪ AB . O‬הוא משיק‬
‫למעגל ו‪ ACD -‬הוא חותך למעגל הנפגש‬
‫‪F‬‬
‫‪B‬‬
‫עם ‪ EF‬בנקודה ‪ . G‬נתון ‪ 6 :‬ס " מ ‪, AB ‬‬
‫‪ 5‬ס " מ ‪ 3 , DC ‬ס " מ ‪ 4 , DG ‬ס " מ ‪. FG ‬‬
‫א ‪ .‬חשב את אורך הקטע ‪. AC‬‬
‫‪O‬‬
‫‪A‬‬
‫‪C‬‬
‫ב ‪ .‬חשב את רדיוס המעגל ‪.‬‬
‫‪G‬‬
‫‪E‬‬
‫‪120‬‬
‫‪D‬‬
‫פתרון ‪:‬‬
‫א ‪ .‬מנקודה ‪ A‬שמחוץ למעגל יוצאים למעגל משיק ‪ AB‬וחותך ‪, ACD‬‬
‫ולכן מתקיים ‪ ) AB2  AD  AC :‬לפי המשפט ‪ :‬אם מנקודה שמחוץ‬
‫למעגל יוצאים למעגל חותך ומשיק ‪ ,‬אז מכפלת החותך בחלקו‬
‫החיצוני שווה לריבוע המשיק (‪ .‬נתון ‪ 6 :‬ס " מ ‪ 5 , AB ‬ס " מ ‪. DC ‬‬
‫נסמן ‪ , AC  x :‬ולכן ‪ . AD  x  5‬ראינו כי ‪. AB2  AD  AC‬‬
‫‪2‬‬
‫נציב ונקבל ‪ 6  x(x  5) :‬ומכאן ‪. x 2  5x  36  0‬‬
‫פתרונות המשוואה הריבועית הם ‪ x  4 :‬או ‪. x  9‬‬
‫הפתרון ‪ x  9‬נפסל ‪ ,‬מכיוון ש‪ x -‬מייצג אורך של קטע ‪.‬‬
‫עבור הפתרון ‪ x  4‬נקבל ‪ 4‬ס " מ ‪. AC  x ‬‬
‫ב ‪ DC .‬ו‪ EF -‬הם שני מיתרים הנחתכים בנקודה ‪ G‬ולכן מתקיים ‪:‬‬
‫‪ ) FG  EG  DG  CG‬לפי המשפט ‪ :‬אם שני מיתרים במעגל נחתכים ‪,‬‬
‫אז מכפלת קטעי מי תר אחד שווה למכפלת קטעי המיתר השני (‪.‬‬
‫נתון ‪ 3 :‬ס " מ ‪ 4 , DG ‬ס " מ ‪. FG ‬‬
‫נחשב את ‪: CG‬‬
‫‪ 2‬ס " מ ‪. CG  DC  DG  5  3 ‬‬
‫ראינו כי ‪. FG  EG  DG  CG‬‬
‫נציב ונקבל ‪ 4  EG  3  2 :‬ומכאן ‪ 1.5‬ס " מ ‪. EG ‬‬
‫נחשב את הקוטר ‪ 5.5 : EF‬ס " מ ‪EF  EG  FG  1.5  4 ‬‬
‫‪1‬‬
‫הרדיוס שווה לחצי מהקוטר ‪ .‬נקבל ‪ 2.75 :‬ס " מ ‪. R  EF  1  5.5 ‬‬
‫‪2‬‬
‫‪2‬‬
‫תרגילים‬
‫‪.1‬‬
‫הוכח ‪ :‬שני מיתרים ה נחתכים במעגל מחלקים זה את זה לשני קטעים‬
‫כך שמכפלת קטעי מיתר אחד שווה למכפלת קטעי המיתר השני ‪.‬‬
‫‪.2‬‬
‫חשב א ת ‪ x‬בשרטוטים הבאים ‪:‬‬
‫א‪.‬‬
‫ב‪.‬‬
‫‪x‬‬
‫‪6‬‬
‫‪x5‬‬
‫‪10‬‬
‫תשובה ‪:‬‬
‫‪3‬‬
‫‪15‬‬
‫‪x‬‬
‫‪12‬‬
‫‪12‬‬
‫א‪. 5 .‬‬
‫ג‪.‬‬
‫ב‪. 4 .‬‬
‫‪12‬‬
‫‪x‬‬
‫‪8‬‬
‫ג‪. 6 .‬‬
‫‪A‬‬
‫‪.3‬‬
‫המיתרים ‪ AC‬ו‪ BD -‬נ חתכים‬
‫‪B‬‬
‫בנקודה ‪ . E‬נתון ‪ 3 :‬ס " מ ‪, AE ‬‬
‫‪ 4‬ס " מ ‪ 6 , BE ‬ס " מ ‪. DE ‬‬
‫‪E‬‬
‫‪D‬‬
‫‪C‬‬
‫חשב את אורך ה מיתר ‪. AC‬‬
‫‪121‬‬
‫תשובה ‪:‬‬
‫‪.4‬‬
‫‪ 11‬ס " מ ‪.‬‬
‫‪C‬‬
‫המיתרים ‪ AB‬ו‪ CD -‬נחתכים בנקודה ‪. P‬‬
‫נתון ‪ 4 :‬ס " מ ‪ 18 , CP ‬ס " מ ‪, DP ‬‬
‫‪B‬‬
‫‪A‬‬
‫‪P‬‬
‫‪ 17‬ס " מ ‪. AP  BP , AB ‬‬
‫חשב את אורך הקטע ‪. AP‬‬
‫תשובה ‪:‬‬
‫‪.5‬‬
‫‪D‬‬
‫‪ 8‬ס"מ‪.‬‬
‫המיתרים ‪ AB‬ו‪ CD -‬נחתכים‬
‫‪C‬‬
‫בנקודה ‪ . P‬נתון ‪ 4 :‬ס " מ ‪, CP ‬‬
‫‪ 18‬ס " מ ‪. 2BP  AP , DP ‬‬
‫‪B‬‬
‫‪A‬‬
‫‪P‬‬
‫חשב את אורך המיתר ‪. AB‬‬
‫תשובה ‪:‬‬
‫‪.6‬‬
‫‪ 18‬ס " מ ‪.‬‬
‫‪D‬‬
‫במעגל שמרכזו ‪ , O‬הקוטר ‪AC‬‬
‫חותך את המיתר ‪ BD‬בנקודה ‪. E‬‬
‫נתון ‪ 6 :‬ס " מ ‪ 4 , BE ‬ס " מ ‪, DE ‬‬
‫‪ 2.5‬ס " מ ‪. OE ‬‬
‫‪A‬‬
‫‪D‬‬
‫‪E‬‬
‫‪O‬‬
‫‪B‬‬
‫חשב את רדיוס המעגל ‪.‬‬
‫תשובה ‪:‬‬
‫‪.7‬‬
‫‪C‬‬
‫‪ 5.5‬ס " מ ‪.‬‬
‫‪D‬‬
‫המיתרים ‪ AB‬ו‪ CD -‬נחתכים‬
‫בנקודה ‪ . P‬נתון ‪, OP  CD :‬‬
‫‪B‬‬
‫‪ 5‬ס " מ ‪ 20 , AP ‬ס " מ ‪. PB ‬‬
‫‪O‬‬
‫חשב את אורך המיתר ‪. CD‬‬
‫תשובה ‪:‬‬
‫‪.8‬‬
‫‪P‬‬
‫‪A‬‬
‫‪C‬‬
‫‪ 20‬ס " מ ‪.‬‬
‫הקוטר ‪ AC‬של מעגל ‪ O‬חותך‬
‫‪D‬‬
‫את המיתר ‪ BD‬בנקודה ‪. E‬‬
‫נתון ‪ 12 , AC  BD :‬ס " מ ‪, BD ‬‬
‫‪A‬‬
‫‪. AC  5CE‬‬
‫‪E‬‬
‫‪C‬‬
‫‪O‬‬
‫חשב את שטח המשולש ‪. AOD‬‬
‫תשובה ‪:‬‬
‫‪B‬‬
‫‪ 22.5‬סמ " ר ‪.‬‬
‫‪122‬‬
‫‪.9‬‬
‫‪C‬‬
‫‪ AB‬ו‪ CD -‬הם שני מיתרים במעגל‬
‫שמרכזו ‪ O‬הנחתכים בנקודה ‪. P‬‬
‫‪P‬‬
‫‪B‬‬
‫‪A‬‬
‫נתון ‪ 4 , AP  BP :‬ס " מ ‪, CP ‬‬
‫‪O‬‬
‫‪ 9‬ס " מ ‪ 8 , DP ‬ס " מ ‪. OP ‬‬
‫חשב את רדיוס המעגל ‪.‬‬
‫תשובה ‪:‬‬
‫‪. 10‬‬
‫‪A‬‬
‫‪M‬‬
‫‪G‬‬
‫‪D‬‬
‫‪F‬‬
‫‪O‬‬
‫‪B‬‬
‫‪ 9‬ס"מ‪.‬‬
‫במעגל שמרכזו ‪ , M‬המיתרים ‪ AB‬ו‪CD -‬‬
‫ניצבים זה לזה ‪ .‬נתון ‪ 2 :‬ס " מ ‪, AE ‬‬
‫‪ 6‬ס " מ ‪ 3 , BE ‬ס " מ ‪. DE ‬‬
‫מצא את מרחק המיתר ‪ AB‬ממרכז המעגל ‪.‬‬
‫תשובה ‪:‬‬
‫‪. 12‬‬
‫‪ 10‬ס " מ ‪.‬‬
‫במעגל שמרכזו ‪ , O‬שני מיתר ים ‪FG‬‬
‫ו‪ AB -‬נחתכים בנקודה ‪ , D‬כך ש הנקודה ‪D‬‬
‫היא אמצע המיתר ‪ . AB‬המיתר ‪ FG‬מאונך‬
‫לרדיוס ‪ AO‬וחותך אותו בנקודה ‪. M‬‬
‫נתון ‪ 24 :‬ס " מ ‪ 3.5 , AB ‬ס " מ ‪. DM ‬‬
‫חשב את אורך הקטע ‪. FD‬‬
‫תשובה ‪:‬‬
‫‪. 11‬‬
‫‪D‬‬
‫‪C‬‬
‫‪M‬‬
‫‪B‬‬
‫‪E‬‬
‫‪ 0.5‬ס " מ ‪.‬‬
‫‪A‬‬
‫‪D‬‬
‫המיתרים ‪ AC‬ו‪ BD -‬נפגשים בנקודה ‪ . E‬נתון ‪. DE  2AE :‬‬
‫הוכח ‪. CE  2BE :‬‬
‫‪. 13‬‬
‫‪ AB‬הוא מיתר במעגל שמרכזו ‪. O‬‬
‫נתון ‪ 16 :‬ס " מ ‪ 9 , AP ‬ס " מ ‪, PB ‬‬
‫‪P‬‬
‫‪B‬‬
‫‪ 5‬ס " מ ‪. OP ‬‬
‫‪O‬‬
‫חשב את רדיוס המעגל ‪.‬‬
‫תשובה ‪:‬‬
‫‪A‬‬
‫‪ 13‬ס " מ ‪.‬‬
‫‪A‬‬
‫‪. 14‬‬
‫‪ AB‬הוא קוטר של מעגל ‪.‬‬
‫‪D‬‬
‫‪ PQ‬מאונך לקוטר ‪. AB‬‬
‫נתון ‪ 3 :‬ס " מ ‪ 12 , CP ‬ס " מ ‪. PD ‬‬
‫חשב את אורך הקטע ‪. PQ‬‬
‫תשובה ‪:‬‬
‫‪Q‬‬
‫‪ 6‬ס"מ‪.‬‬
‫‪P‬‬
‫‪B‬‬
‫‪123‬‬
‫‪C‬‬
‫‪. 15‬‬
‫במעגל שלפניך המיתר ‪ EF‬חותך את‬
‫‪B‬‬
‫‪A‬‬
‫המיתרים ‪ AD‬ו‪ BC -‬בנקודות ‪ G‬ו‪. H -‬‬
‫נתון ‪ 5 :‬ס " מ ‪ 6 , AG ‬ס " מ ‪, DG ‬‬
‫‪ 3‬ס " מ ‪ 4 , EG ‬ס " מ ‪. CH  BH , FH ‬‬
‫‪F‬‬
‫‪E‬‬
‫‪G‬‬
‫‪H‬‬
‫א ‪ .‬חשב את אורך המיתר ‪. EF‬‬
‫‪C‬‬
‫ב ‪ .‬חשב את אורך המיתר ‪. BC‬‬
‫תשובה ‪:‬‬
‫‪. 16‬‬
‫ב ‪ 12 .‬ס " מ ‪.‬‬
‫המשולש ‪ ABC‬חסום במעגל ‪ .‬המיתר ‪ST‬‬
‫חותך את הצלעות ‪ AB‬ו‪ AC -‬בנקודות ‪ P‬ו‪. Q -‬‬
‫נתון ‪ 10 , AQ  CQ , AP  BP :‬ס " מ ‪, BC ‬‬
‫‪ 2‬ס " מ ‪ 3 , TP ‬ס " מ ‪. QS ‬‬
‫א ‪ .‬חשב את אורך הצלע ‪. AB‬‬
‫ב ‪ .‬חשב את אורך הצלע ‪. AC‬‬
‫תשובה ‪:‬‬
‫‪. 17‬‬
‫א ‪ 13 .‬ס " מ ‪.‬‬
‫‪D‬‬
‫‪A‬‬
‫‪S‬‬
‫‪Q‬‬
‫‪P‬‬
‫‪C‬‬
‫‪B‬‬
‫א ‪ 8 .‬ס " מ ‪ .‬ב ‪ 9.165 .‬ס " מ ‪.‬‬
‫‪ AB‬הוא קוטר ב מעגל שמרכזו ‪. O‬‬
‫‪C‬‬
‫‪ CD‬הוא מיתר המאונך לקוטר ‪. AB‬‬
‫נתון ‪ 12 :‬ס " מ ‪ 3 , AK ‬ס " מ ‪, KB ‬‬
‫‪ 10‬ס " מ ‪. PC ‬‬
‫‪P‬‬
‫‪B‬‬
‫‪K‬‬
‫‪O‬‬
‫חשב את אורך הקטע ‪. PQ‬‬
‫תשובה ‪:‬‬
‫‪. 18‬‬
‫‪T‬‬
‫‪A‬‬
‫‪Q‬‬
‫‪D‬‬
‫‪ 4.4‬ס " מ ‪.‬‬
‫המ שולש ‪ ABC‬חסום במעגל ‪ AD .‬ו‪BE -‬‬
‫‪A‬‬
‫הם תיכונים במשולש הנפגשים בנקודה ‪. F‬‬
‫המשכי התיכונים חותכים את המעגל‬
‫‪H‬‬
‫‪E‬‬
‫בנקודות ‪ G‬ו‪ . H -‬נתון ‪ 24 :‬ס " מ ‪, BC ‬‬
‫‪ 8‬ס " מ ‪. BF  GF , DG ‬‬
‫‪F‬‬
‫‪C‬‬
‫חשב את אורך הצלע ‪. AC‬‬
‫‪B‬‬
‫‪D‬‬
‫‪G‬‬
‫תשובה ‪:‬‬
‫‪. 19‬‬
‫‪ 20.49‬ס " מ ‪.‬‬
‫‪A‬‬
‫המשולש ‪ ABC‬הוא שווה‪ -‬שוקיים )‪. (AB  AC‬‬
‫‪ O‬מרכז המעגל ‪ OP .‬מאונך ל‪. AC -‬‬
‫‪P‬‬
‫‪ OD‬מאונך ל‪ . BC -‬נתון ‪ 32 :‬ס " מ ‪, AD ‬‬
‫‪ 18‬ס " מ ‪ . DE ‬חשב את אורך הקטע ‪. OP‬‬
‫תשובה ‪:‬‬
‫‪ 15‬ס " מ ‪.‬‬
‫‪O‬‬
‫‪C‬‬
‫‪D‬‬
‫‪E‬‬
‫‪124‬‬
‫‪B‬‬
‫‪. 20‬‬
‫‪A‬‬
‫המיתר ‪ PQ‬מק ביל למיתר ‪. BC‬‬
‫נתון ‪ 6 :‬ס " מ ‪ 16 , AT ‬ס " מ ‪, AB ‬‬
‫‪S‬‬
‫‪P‬‬
‫‪ 12‬ס " מ ‪ 1.5 , BC ‬ס " מ ‪. SP ‬‬
‫‪T‬‬
‫‪Q‬‬
‫חשב את אורך המיתר ‪. PQ‬‬
‫תשובה ‪:‬‬
‫‪. 21‬‬
‫‪C‬‬
‫‪ 16‬ס " מ ‪.‬‬
‫הנקודות ‪ C , B , A‬ו‪ D -‬נמצאות על מעגל ‪.‬‬
‫נתון ‪ 16 , AB  CD :‬ס " מ ‪ 32 , AB ‬ס " מ ‪, CE ‬‬
‫‪B‬‬
‫‪A‬‬
‫‪ 27‬ס " מ ‪ 12 , AC ‬ס " מ ‪. BG ‬‬
‫‪G‬‬
‫א ‪ .‬חשב את אורך הקטע ‪. AG‬‬
‫ב ‪ .‬חשב את אורך הקטע ‪. GF‬‬
‫תשובה ‪:‬‬
‫‪. 22‬‬
‫‪B‬‬
‫א‪ 9 .‬ס"מ‪.‬‬
‫‪D‬‬
‫‪C‬‬
‫‪E‬‬
‫ב ‪ 13.5 .‬ס " מ ‪.‬‬
‫שני מעגלים נחתכים בנקודות ‪ P‬ו‪. Q -‬‬
‫הקטע ‪ AD‬חותך מעגל אחד בנקודות‬
‫‪ A‬ו‪ , C -‬מעגל שני בנקודות ‪ B‬ו‪D -‬‬
‫ואת המיתר ‪ PQ‬בנקודה ‪. K‬‬
‫א ‪ .‬הוכח ‪. BK  DK  AK  CK :‬‬
‫ב ‪ .‬נתון ‪ 8 :‬ס " מ ‪ 2 , CD ‬ס " מ ‪, CK ‬‬
‫‪ 4‬ס " מ ‪ . AB ‬חשב את אורך הקטע ‪. BK‬‬
‫תשובה ‪:‬‬
‫‪F‬‬
‫‪P‬‬
‫‪D‬‬
‫‪K C‬‬
‫‪B‬‬
‫‪A‬‬
‫‪Q‬‬
‫ב‪ 1 .‬ס"מ‪.‬‬
‫‪A‬‬
‫‪. 23‬‬
‫ה משולש ‪ ABC‬חסום במעגל ‪.‬‬
‫‪AB 4‬‬
‫‪,‬‬
‫‪ AP‬חוצה את ה זווית ‪ . BAC‬נתון ‪ :‬‬
‫‪AC 3‬‬
‫‪ 14‬ס " מ ‪ 4 , BC ‬ס " מ ‪. PQ ‬‬
‫חשב את אורך הקטע ‪. AP‬‬
‫תשובה ‪:‬‬
‫‪. 24‬‬
‫‪C‬‬
‫‪ 12‬ס " מ ‪.‬‬
‫‪P‬‬
‫‪B‬‬
‫‪Q‬‬
‫הוכח ‪ :‬אם מנקודה שמחוץ למעגל יוצאים שני חותכים למעגל ‪ ,‬אז מכפלת‬
‫חותך אחד בחלקו החיצוני שווה למכפלת החותך השני בחלקו החיצוני ‪.‬‬
‫‪. 25‬‬
‫חשב את ‪ x‬בשרטוטים הבאים ‪:‬‬
‫א‪.‬‬
‫ב‪.‬‬
‫‪7‬‬
‫‪5‬‬
‫‪6‬‬
‫‪x‬‬
‫‪8‬‬
‫‪10‬‬
‫‪125‬‬
‫‪10‬‬
‫‪x‬‬
‫‪3‬‬
‫‪5‬‬
‫ג‪.‬‬
‫‪x‬‬
‫תשובה ‪:‬‬
‫‪. 26‬‬
‫א‪. 6 .‬‬
‫ד‪.‬‬
‫‪x 1‬‬
‫‪x‬‬
‫‪6‬‬
‫ב‪ . 4 .‬ג‪. 4 .‬‬
‫‪7‬‬
‫‪10‬‬
‫ד‪. 8 .‬‬
‫המשכי הקוטר ‪ AB‬והמיתר ‪ DC‬נפגשים‬
‫בנקודה ‪ . E‬נתון ‪ 12 :‬ס " מ ‪, CE ‬‬
‫‪ 10‬ס " מ ‪ 9 , CD ‬ס " מ ‪. BE ‬‬
‫‪B‬‬
‫‪A‬‬
‫חשב את רדיוס המעגל ‪.‬‬
‫תשובה ‪:‬‬
‫‪. 27‬‬
‫‪C‬‬
‫‪ 10 1‬ס " מ ‪.‬‬
‫‪6‬‬
‫‪D‬‬
‫‪ DC‬הוא קוטר במעגל שמרכזו ‪. O‬‬
‫המשכי הקוטר ‪ DC‬והמיתר ‪BA‬‬
‫נחתכים בנקודה ‪. P‬‬
‫נתון ‪ 17 :‬ס " מ ‪ 12 , AB ‬ס " מ ‪, CP ‬‬
‫‪ . AP  CO‬חשב את רדיוס המעגל ‪.‬‬
‫תשובה ‪:‬‬
‫‪. 28‬‬
‫‪B‬‬
‫‪A‬‬
‫‪P‬‬
‫‪D‬‬
‫‪O‬‬
‫‪C‬‬
‫‪ 16‬ס " מ ‪.‬‬
‫‪ PCD‬ו‪ PAB -‬הם שני חותכים למעגל ‪.‬‬
‫‪B‬‬
‫נתון ‪. CP  2AP , AB  5AP :‬‬
‫‪A‬‬
‫‪P‬‬
‫חשב את היחס ‪. DC : BP‬‬
‫תשובה ‪:‬‬
‫‪. 29‬‬
‫‪E‬‬
‫‪C‬‬
‫‪.1‬‬
‫‪6‬‬
‫‪D‬‬
‫‪ ABC‬ו‪ ADE -‬הם שני חותכים למעגל ‪.‬‬
‫נתון ‪. 3  AB  4  AD :‬‬
‫א ‪ .‬הוכח ‪. AC  3  AE :‬‬
‫‪4‬‬
‫ב ‪ .‬נתון ‪ 9 :‬ס " מ ‪ 3 , AC ‬ס " מ ‪. AB ‬‬
‫חשב את א ורך הקטע ‪. DE‬‬
‫תשובה ‪:‬‬
‫ב ‪ 9.75 .‬ס " מ ‪.‬‬
‫‪126‬‬
‫‪C‬‬
‫‪B‬‬
‫‪D‬‬
‫‪E‬‬
‫‪A‬‬
‫‪. 30‬‬
‫מנקודה ‪ P‬יוצאים למעגל שני חותכים ‪:‬‬
‫‪B‬‬
‫‪A‬‬
‫חותך ‪ PAB‬וחותך ‪. PCD‬‬
‫‪P‬‬
‫נתון ‪. PA  PC :‬‬
‫‪C‬‬
‫הוכח ‪. AB  CD :‬‬
‫‪. 31‬‬
‫‪D‬‬
‫‪D‬‬
‫הנקודות ‪ B , A‬ו‪ C -‬נמצאות על מעגל‬
‫שמרכזו ‪ . O‬המשכי המיתר ‪AB‬‬
‫‪C‬‬
‫והרדיוס ‪ OC‬נפגשים בנקודה ‪. D‬‬
‫‪B‬‬
‫נתון ‪ 5 :‬ס " מ ‪ 4 , AO  BD ‬ס " מ ‪. DC ‬‬
‫חשב את אורך המיתר ‪. AB‬‬
‫‪A‬‬
‫‪O‬‬
‫תשובה ‪:‬‬
‫‪. 32‬‬
‫‪ 6.2‬ס " מ ‪.‬‬
‫המשולש ‪ ABO‬הוא משולש שווה‪ -‬שוקיים‬
‫)‪ . (AO  AB‬הנקודה ‪ O‬היא מרכז המעגל ‪.‬‬
‫‪O‬‬
‫נתון ‪ 25 :‬ס " מ ‪ 15 , AO ‬ס " מ ‪. BO ‬‬
‫חשב את אורך הקטעים ‪ AP‬ו‪. PB -‬‬
‫תשובה ‪:‬‬
‫‪. 33‬‬
‫‪A‬‬
‫‪P‬‬
‫‪ 16‬ס " מ ‪ 9 ,‬ס " מ ‪.‬‬
‫‪B‬‬
‫‪A‬‬
‫המשולש ‪ ABO‬הוא ישר‪ -‬זווית ) ‪. (O  90‬‬
‫‪P‬‬
‫נקודה ‪ O‬היא מרכז המעגל ‪.‬‬
‫‪Q‬‬
‫נתון ‪ 21 :‬ס " מ ‪ 35 , OQ ‬ס " מ ‪. AB ‬‬
‫‪B‬‬
‫חשב את אורכי הקטעים ‪ AP‬ו‪. PB -‬‬
‫תשובה ‪:‬‬
‫‪. 34‬‬
‫‪O‬‬
‫‪ 9.8‬ס " מ ‪ 25.2 ,‬ס " מ ‪.‬‬
‫מנקודה ‪ A‬יוצא חותך למעגל ‪.‬‬
‫‪C‬‬
‫נתון כי רדיוס המעגל הוא ‪ 3‬וכי ערך‬
‫המכפלה ‪ AB  AC‬הוא ‪. 16‬‬
‫חשב את מרחק הנקודה ‪ A‬ממרכז המעגל ‪.‬‬
‫תשובה ‪:‬‬
‫‪.5‬‬
‫‪127‬‬
‫‪A‬‬
‫‪B‬‬
‫‪. 35‬‬
‫‪A‬‬
‫נתון משולש שווה‪ -‬שוקיים ‪. (AB  AC) ABC‬‬
‫‪ AB‬הוא קו טר המעגל שמרכזו ‪. M‬‬
‫מעגל זה חותך את ‪ BC‬בנקודה ‪ D‬ואת‬
‫‪M‬‬
‫‪ AC‬בנקודה ‪ . E‬נתון ‪ 13 :‬ס " מ ‪, AB ‬‬
‫‪E‬‬
‫‪ 10‬ס " מ ‪ . BC ‬חשב את אורך הקטע ‪. CE‬‬
‫תשובה ‪:‬‬
‫‪. 36‬‬
‫‪C‬‬
‫‪ 3 11‬ס " מ ‪.‬‬
‫‪13‬‬
‫‪‬‬
‫המשולש ‪ ABC‬הוא ישר‪ -‬זווית ) ‪. (C  90‬‬
‫‪D‬‬
‫‪A‬‬
‫נתון ‪ 12 :‬ס " מ ‪ 8 , BP ‬ס " מ ‪. PC ‬‬
‫‪Q‬‬
‫אורך רדיוס המעגל הוא ‪ 8.5‬ס " מ ‪.‬‬
‫חשב את אורך הקטע ‪. BQ‬‬
‫תשובה ‪:‬‬
‫‪. 37‬‬
‫‪C‬‬
‫‪P‬‬
‫‪ 9.6‬ס " מ ‪.‬‬
‫‪E‬‬
‫‪ 8‬ס " מ ‪ 4 , AP ‬ס " מ ‪, FQ ‬‬
‫‪B‬‬
‫‪A‬‬
‫‪Q‬‬
‫‪P‬‬
‫‪ 5‬ס " מ ‪. AQ  BQ , QE ‬‬
‫חשב את אורך הקטע ‪. AQ‬‬
‫‪. 38‬‬
‫‪B‬‬
‫בציור נתון ‪ 10 :‬ס " מ ‪ 6 , CP ‬ס " מ ‪, CD ‬‬
‫תשובה ‪:‬‬
‫‪B‬‬
‫‪C‬‬
‫‪F‬‬
‫‪D‬‬
‫‪ 10‬ס " מ ‪.‬‬
‫‪A‬‬
‫‪ PQ‬מקביל לצלע ‪ BC‬במשולש ‪. ABC‬‬
‫הצלעות ‪ AB‬ו‪ AC -‬חותכות את המעגל‬
‫בנקודות ‪ Q‬ו‪ . M -‬נתון ‪ 27 :‬ס " מ ‪, PQ ‬‬
‫‪M‬‬
‫‪ 45‬ס " מ ‪ 20 , BC ‬ס " מ ‪ 24 , BQ ‬ס " מ ‪. PC ‬‬
‫‪P‬‬
‫חשב את אורך הקטע ‪. MP‬‬
‫תשובה ‪:‬‬
‫‪. 39‬‬
‫‪Q‬‬
‫‪C‬‬
‫‪ 11‬ס " מ ‪.‬‬
‫‪B‬‬
‫‪C‬‬
‫שני מעגלים נחתכים בנקודות ‪ A‬ו‪. B -‬‬
‫‪ CH‬הוא חותך למעגל הימני‬
‫‪G‬‬
‫ו‪ CF -‬חותך למעגל השמאלי ‪.‬‬
‫‪A‬‬
‫‪E‬‬
‫א ‪ .‬הוכח ‪. CE  CF  CG  CH :‬‬
‫ב ‪ .‬נתו ן ‪. CE  CF  60 , GH  7 :‬‬
‫‪H‬‬
‫חשב את אורך החותך ‪. CH‬‬
‫תשובה ‪:‬‬
‫‪B‬‬
‫ב ‪. 12 .‬‬
‫‪128‬‬
‫‪F‬‬
‫‪. 40‬‬
‫‪A‬‬
‫‪ CP‬הוא חוצה‪ -‬הזווית של ‪ ACB‬במשולש ‪. ABC‬‬
‫המעגל חותך את הצלעות ‪ AB‬ו‪AC -‬‬
‫בנקודות ‪ P‬ו‪ . Q -‬נתון ‪ 24 :‬ס " מ ‪, AB ‬‬
‫‪ 25‬ס " מ ‪ 15 , AC ‬ס " מ ‪. BC ‬‬
‫חשב את אורך הקטע ‪. AQ‬‬
‫תשובה ‪:‬‬
‫‪. 41‬‬
‫‪Q‬‬
‫‪P‬‬
‫‪C‬‬
‫‪B‬‬
‫‪ 14.4‬ס " מ ‪.‬‬
‫הוכח ‪ :‬אם מנקודה שמחוץ למעגל יוצאים למעגל משיק וחותך ‪,‬‬
‫אז מכפלת החותך בחלקו החיצוני שווה לריבוע המשיק ‪.‬‬
‫‪. 42‬‬
‫בכל אחד מהשרטוטים הבאים מופיע חותך ומשיק למעגל ‪ .‬חשב את ‪. x‬‬
‫א‪.‬‬
‫ג‪.‬‬
‫ב‪.‬‬
‫‪10‬‬
‫‪x‬‬
‫‪3‬‬
‫תשובה ‪:‬‬
‫‪. 43‬‬
‫‪8‬‬
‫‪x‬‬
‫‪9‬‬
‫‪x‬‬
‫‪5‬‬
‫‪12‬‬
‫א ‪ . 6 .‬ב ‪ . 15 .‬ג ‪. 4 .‬‬
‫הנקודות ‪ C , B‬ו‪ D -‬נמצאות על מעגל ‪.‬‬
‫‪D‬‬
‫‪ AB‬משיק למעגל בנקודה ‪ACD . B‬‬
‫הוא חותך למעגל ‪ .‬נתון ‪ 2 :‬ס " מ ‪, AB ‬‬
‫‪ 3‬ס " מ ‪ . DC ‬חשב את אורך הקטע ‪. AD‬‬
‫תשובה ‪:‬‬
‫‪C‬‬
‫‪A‬‬
‫‪B‬‬
‫‪ 4‬ס"מ‪.‬‬
‫‪A‬‬
‫‪. 44‬‬
‫המשולש ‪ ABC‬הוא שווה‪ -‬שוקיים )‪. (AB  AC‬‬
‫הצלע ‪ BC‬משיקה למעגל בנקודה ‪. B‬‬
‫נתון ‪ 10 :‬ס " מ ‪ 20 , BC ‬ס " מ ‪. AB ‬‬
‫חשב את אורך הקטע ‪. AP‬‬
‫‪P‬‬
‫‪ 15‬ס " מ ‪.‬‬
‫‪C‬‬
‫תשובה ‪:‬‬
‫‪. 45‬‬
‫‪B‬‬
‫‪ AP‬הוא משיק למעגל ‪ .‬הקטע המחבר‬
‫‪P‬‬
‫את הנקודה ‪ A‬עם מרכז המעגל ‪,‬‬
‫חותך את המעגל בנקודה ‪. Q‬‬
‫נתון ‪ 12 :‬ס " מ ‪ 8 , AP ‬ס " מ ‪. AQ ‬‬
‫חשב את רדיוס המעגל ‪.‬‬
‫‪129‬‬
‫‪A‬‬
‫‪Q‬‬
‫‪O‬‬
‫תשובה ‪:‬‬
‫‪. 46‬‬
‫‪ 5‬ס"מ‪.‬‬
‫‪ AD‬הוא קוטר של מעגל ‪.‬‬
‫‪B‬‬
‫‪ AB‬משיק למעגל בנקודה ‪. A‬‬
‫‪C‬‬
‫נתון ‪ 15 :‬ס " מ ‪ 16 , AB ‬ס " מ ‪. DC ‬‬
‫א ‪ .‬חשב את אורך הקטע ‪. BC‬‬
‫‪D‬‬
‫ב ‪ .‬חשב את רדיוס המעגל ‪.‬‬
‫תשובה ‪:‬‬
‫‪. 47‬‬
‫‪A‬‬
‫א ‪ 9 .‬ס " מ ‪ .‬ב ‪ 10 .‬ס " מ ‪.‬‬
‫‪A‬‬
‫במשולש ‪ , ABC‬הצלע ‪ BC‬משיקה למעגל‬
‫‪Q‬‬
‫בנקודה ‪ B‬והצלע ‪ AC‬משיקה למעגל‬
‫בנקודה ‪ . P‬נתון ‪ 25 :‬ס " מ ‪, AB ‬‬
‫‪P‬‬
‫‪ 29‬ס " מ ‪ 19 , AC ‬ס " מ ‪. BC ‬‬
‫חשב את אור ך הקטע ‪. AQ‬‬
‫תשובה ‪:‬‬
‫‪. 48‬‬
‫‪ 4‬ס"מ‪.‬‬
‫‪B‬‬
‫‪C‬‬
‫‪A‬‬
‫‪ BC‬משיק בנקודה ‪ C‬למעגל שמרכזו ‪, O‬‬
‫‪D‬‬
‫ו‪ AB -‬משיק למעגל בנקודה ‪. P‬‬
‫‪P‬‬
‫‪ CD‬הוא קוטר המעגל ‪ .‬נתון ‪ 2 :‬ס " מ ‪, AD ‬‬
‫‪ 3‬ס " מ ‪ . OD ‬חשב את אורך הקטע ‪. AB‬‬
‫תשובה ‪:‬‬
‫‪O‬‬
‫‪ 10‬ס " מ ‪.‬‬
‫‪C‬‬
‫‪B‬‬
‫‪. 49‬‬
‫שני מעגלים משיקים זה לזה מבפנים‬
‫‪B‬‬
‫בנקודה ‪ . B‬מנקודה ‪ A‬שמחוץ למעגלים‬
‫‪A‬‬
‫‪C‬‬
‫מעבירים חותך ‪ ACE‬למעגל הגדול ‪.‬‬
‫חותך זה משיק למעגל הקטן בנקודה ‪. D‬‬
‫‪D‬‬
‫הקטע ‪ AB‬הוא משיק משותף לשני‬
‫המעגלים ‪ .‬נתון ‪. AB  DE :‬‬
‫הוכח ‪ :‬א ‪ . AB  1 AE .‬ב ‪. CD  1 DE .‬‬
‫‪2‬‬
‫‪2‬‬
‫‪. 50‬‬
‫‪E‬‬
‫הנקודות ‪ B , A‬ו‪ C -‬נמצאות על מעגל ‪. O‬‬
‫‪ DC‬משיק למעגל בנקודה ‪ . C‬נתון ‪, OC  AB :‬‬
‫‪ 4‬ס " מ ‪ 2 , DC ‬ס " מ ‪. BD ‬‬
‫‪C‬‬
‫א ‪ .‬חשב את אורך המיתר ‪. AB‬‬
‫‪O‬‬
‫ב ‪ .‬חשב את שטח הטרפז ‪. AOCD‬‬
‫תשובה ‪:‬‬
‫א‪ 6 .‬ס"מ‪.‬‬
‫ב ‪ 26 .‬סמ " ר ‪.‬‬
‫‪130‬‬
‫‪B D‬‬
‫‪A‬‬
‫‪. 51‬‬
‫הצלעות ‪ AC‬ו‪ BC -‬של משולש ‪ABC‬‬
‫נוגעות במעגל בנקודות ‪ F‬ו‪. G -‬‬
‫הצלע ‪ AB‬חותכת את המעגל בנקודות‬
‫‪ D‬ו‪ . E -‬נתון ‪ 4 :‬ס " מ ‪, AF ‬‬
‫‪ 6‬ס " מ ‪ 3 3 , DE ‬ס " מ ‪. BG ‬‬
‫חשב את אורך הצלע ‪. AB‬‬
‫תשובה ‪:‬‬
‫‪. 52‬‬
‫‪A‬‬
‫‪D‬‬
‫‪F‬‬
‫‪E‬‬
‫‪C‬‬
‫‪ 11‬ס " מ ‪.‬‬
‫‪B‬‬
‫‪G‬‬
‫ה משולש ‪ ABC‬הוא שווה‪ -‬צלעות ‪.‬‬
‫‪A‬‬
‫הצלע ‪ BC‬משיקה למעגל בנקודה ‪, P‬‬
‫והצלעות ‪ AB‬ו‪ AC -‬חותכות את המעגל‬
‫בנקודות ‪ Q‬ו‪ S -‬בהתאמה ‪.‬‬
‫נתון ‪ 18 :‬ס " מ ‪ 10 , BC ‬ס " מ ‪. AQ ‬‬
‫‪S‬‬
‫חשב את אורך הקטע ‪. AS‬‬
‫תשובה ‪:‬‬
‫‪. 53‬‬
‫‪Q‬‬
‫‪C‬‬
‫‪B‬‬
‫‪P‬‬
‫‪ 16‬ס " מ ‪.‬‬
‫‪A‬‬
‫ה משולש ‪ ABC‬הוא שווה‪ -‬צלעות ‪.‬‬
‫הצלע ‪ BC‬משיקה למעגל בנקודה ‪, P‬‬
‫והצלעות ‪ AB‬ו‪ AC -‬חותכות את המעגל‬
‫בנקודות ‪ Q‬ו‪ S -‬בהתאמה ‪.‬‬
‫‪Q‬‬
‫‪S‬‬
‫נתון ‪ . BP  CP :‬הוכח ‪. AQ  1.5PC :‬‬
‫‪C‬‬
‫‪. 54‬‬
‫‪B‬‬
‫‪P‬‬
‫מנקודה ‪ , B‬שמחוץ למעגל ‪ , O‬יוצ אים‬
‫שני ישרים ‪ .‬ישר אחד משיק למעגל‬
‫בנקודה ‪ , A‬וישר שני חותך את‬
‫המעגל בנקודות ‪ C‬ו‪ E -‬ואת הקוטר ‪GF‬‬
‫בנקודה ‪ . D‬נתון ‪ 6 :‬ס " מ ‪, AB ‬‬
‫‪ 3‬ס " מ ‪ 2 , BC  CD ‬ס " מ ‪. OD ‬‬
‫א ‪ .‬חשב את אורך הקטע ‪. DE‬‬
‫ב ‪ .‬חשב את רדיוס המעגל ‪.‬‬
‫תשובה ‪ :‬א ‪ 6 .‬ס " מ ‪ .‬ב ‪22 .‬‬
‫ס"מ‪.‬‬
‫‪131‬‬
‫‪G‬‬
‫‪B‬‬
‫‪C‬‬
‫‪D‬‬
‫‪E‬‬
‫‪O‬‬
‫‪A‬‬
‫‪F‬‬
‫‪. 55‬‬
‫‪ AD‬הוא קוטר ו‪ BC -‬הוא מיתר במעגל‬
‫שמרכזו ‪ . O‬המשכי הקטעים ‪ AD‬ו‪BC -‬‬
‫נפגשים בנקודה ‪ . E‬נתון ‪ 10 :‬ס " מ ‪, BC ‬‬
‫‪ 6‬ס " מ ‪CE  4 , ED ‬‬
‫‪.‬‬
‫‪AD 9‬‬
‫‪B‬‬
‫‪C‬‬
‫‪E‬‬
‫‪A‬‬
‫‪D‬‬
‫חשב את אורך המשיק היוצא‬
‫מנקודה ‪ E‬אל המעגל ‪.‬‬
‫תשובה ‪:‬‬
‫‪. 56‬‬
‫‪ 12‬ס " מ ‪.‬‬
‫‪ BC‬הוא מיתר במעגל ‪ AB .‬משיק‬
‫‪A‬‬
‫למעגל בנקודה ‪ . B‬הקטע ‪ AC‬חותך‬
‫‪F‬‬
‫את המעגל בנקו דה ‪ . F‬נתון ‪, DE  BC :‬‬
‫‪D‬‬
‫‪E‬‬
‫‪ 6‬ס " מ ‪ 8 , AD  DB ‬ס " מ ‪. AF ‬‬
‫א ‪ .‬חשב את אורך הקטע ‪. CF‬‬
‫‪B‬‬
‫‪C‬‬
‫ב ‪ .‬חשב את אורך הק טע ‪. EF‬‬
‫תשובה ‪:‬‬
‫‪. 57‬‬
‫א ‪ 10 .‬ס " מ ‪ .‬ב ‪ 1 .‬ס " מ ‪.‬‬
‫שני מעגלים משיקים זה לזה מבפנים בנקודה ‪. B‬‬
‫מ נקודה ‪ , A‬ה נמצאת מחוץ לשני המעגלים ‪,‬‬
‫מעבירים קטע החותך את המעגל הגדול בנקודות‬
‫‪F‬‬
‫‪ C‬ו‪ F -‬ו את המעגל הקטן בנקודות ‪ D‬ו‪. E -‬‬
‫הקטע ‪ AB‬הוא משיק משותף לשני המעגלים ‪.‬‬
‫‪E‬‬
‫נתון ‪ 2 :‬ס " מ ‪ 6 , AC ‬ס " מ ‪ 1 , CF ‬ס " מ ‪. DC ‬‬
‫‪C‬‬
‫א ‪ .‬חשב את אורך המשיק ‪. AB‬‬
‫‪A‬‬
‫ב ‪ .‬חשב את אורך הקטע ‪. DE‬‬
‫תשובה ‪:‬‬
‫‪. 58‬‬
‫א‪ 4 .‬ס"מ‪.‬‬
‫‪D‬‬
‫‪B‬‬
‫ב‪ 2 1 .‬ס"מ‪.‬‬
‫‪3‬‬
‫המיתרים ‪ AC‬ו‪ BD -‬נפגשים בנקודה ‪. E‬‬
‫המשיק למעגל בנקודה ‪ C‬נפגש עם המשך‬
‫המיתר ‪ BD‬בנקודה ‪ . G‬נתון ‪ 8 :‬ס " מ ‪, CG ‬‬
‫‪B‬‬
‫‪C‬‬
‫‪ 12‬ס " מ ‪ 5 , BD ‬ס " מ ‪. AE ‬‬
‫‪E‬‬
‫הקטע ‪ GE‬גדול ב‪ 2 -‬ס " מ מהקטע ‪. CE‬‬
‫‪D‬‬
‫חשב את אורך הקטע ‪. DE‬‬
‫‪G‬‬
‫תשובה ‪:‬‬
‫‪ 2‬ס " מ או ‪ 5‬ס " מ ‪.‬‬
‫‪132‬‬
‫‪A‬‬
‫‪. 59‬‬
‫‪A‬‬
‫שני מעגלים משיקים זה לזה בנקודה ‪. B‬‬
‫נקודה ‪ A‬נמצאת מחוץ לשני המעגלים ‪.‬‬
‫‪C‬‬
‫‪E‬‬
‫‪ ACD‬ו‪ AEF -‬הם חותכים למע גלים ‪.‬‬
‫א ‪ .‬הוכח ‪. AE  AF  AC  AD :‬‬
‫ב ‪ .‬נתון ‪ 3 :‬ס " מ ‪ 5 , AE ‬ס " מ ‪, FE ‬‬
‫‪D‬‬
‫‪F‬‬
‫‪B‬‬
‫‪ 2‬ס " מ ‪ . CD ‬חשב את אורך החותך ‪. AD‬‬
‫תשובה ‪:‬‬
‫ב‪ 6 .‬ס"מ‪.‬‬
‫‪P‬‬
‫‪. 60‬‬
‫שני מעגלים נחתכים בנקודות ‪ A‬ו‪. B -‬‬
‫‪C‬‬
‫‪A‬‬
‫נקודה ‪ P‬נמצאת על המשך הקטע ‪. AB‬‬
‫‪D‬‬
‫‪ PD‬משיק למעגל הקטן ו‪ PC -‬משיק‬
‫למעגל הגדול ‪ .‬הוכח ‪. PD  PC :‬‬
‫‪B‬‬
‫‪. 61‬‬
‫‪A‬‬
‫שני מעגלים משיקים חיצונית בנקודה ‪. P‬‬
‫‪D‬‬
‫‪ AC‬ו‪ AE -‬הם שני חותכים למעגלים ‪.‬‬
‫המשיק למעגלים בנקודה ‪P‬‬
‫עובר דרך נקודה ‪. A‬‬
‫נתון ‪ . AB  AD :‬הוכח ‪. BC  DE :‬‬
‫‪. 62‬‬
‫‪B‬‬
‫‪P‬‬
‫‪E‬‬
‫‪C‬‬
‫נתונים שני מעגלים בעלי מרכז משותף ‪. O‬‬
‫‪ AB‬הוא מיתר במעגל הגדול ‪ ,‬המשיק‬
‫‪F‬‬
‫‪D‬‬
‫למעגל הקטן בנקודה ‪ AF . P‬חותך את‬
‫המעגל הקטן בנקודות ‪ E‬ו‪, F -‬‬
‫ו‪ BD -‬חותך אותו בנקודות ‪ C‬ו‪. D -‬‬
‫‪C‬‬
‫א ‪ .‬הוכח ‪. AP  BP :‬‬
‫‪B‬‬
‫ב ‪ .‬הוכח ‪. BC  BD  AE  AF :‬‬
‫‪. 63‬‬
‫הצלעות ‪ AB‬ו‪ AC -‬של משולש ‪ABC‬‬
‫חותכות מעגל בנקודות ‪ D‬ו‪. E -‬‬
‫הצלע ‪ BC‬משיקה למעגל בנקודה ‪. F‬‬
‫נתון ‪ 5 , BAF  CAF :‬ס " מ ‪, AD ‬‬
‫‪ 11‬ס " מ ‪ 5 , BC ‬ס " מ ‪. CF ‬‬
‫חשב את אורך הצלע ‪. AC‬‬
‫תשובה ‪:‬‬
‫‪O‬‬
‫‪133‬‬
‫‪A‬‬
‫‪A‬‬
‫‪D‬‬
‫‪E‬‬
‫‪C‬‬
‫‪ 7.5‬ס " מ ‪.‬‬
‫‪P‬‬
‫‪E‬‬
‫‪F‬‬
‫‪B‬‬
‫‪. 64‬‬
‫‪ ABC‬הוא משולש שווה‪ -‬שוקיים )‪(AB  AC‬‬
‫החסום במעגל ‪ PC .‬הוא משיק למעגל‬
‫בנקודה ‪ , C‬החותך את המשך ‪ BA‬בנקודה ‪. P‬‬
‫נתון ‪ 12 :‬ס " מ ‪ 15 , PC ‬ס " מ ‪. BC ‬‬
‫חשב את אורך הקטע ‪. AP‬‬
‫תשובה ‪:‬‬
‫‪. 65‬‬
‫‪P‬‬
‫‪A‬‬
‫‪C‬‬
‫‪B‬‬
‫‪ 8‬ס"מ‪.‬‬
‫‪ PK‬הוא משיק למעגל ‪ AB ,‬הוא קו טר‬
‫‪K‬‬
‫המעגל ‪ OL ,‬הוא רדיוס המאונך לקוטר ‪, AB‬‬
‫והקטע ‪ LK‬חותך את הקוטר בנקודה ‪. C‬‬
‫א ‪ .‬הוכח ‪. PC  PK :‬‬
‫‪O‬‬
‫‪P‬‬
‫‪B‬‬
‫‪C‬‬
‫‪A‬‬
‫ב ‪ .‬הוכח ‪. PC 2  PA  PB :‬‬
‫‪L‬‬
‫‪. 66‬‬
‫‪A‬‬
‫משולש ‪ ABC‬חסום במעגל ‪.‬‬
‫‪ CD‬ו‪ EP -‬הם משיקים למעגל ‪.‬‬
‫‪P‬‬
‫נתון ‪. DE  BC :‬‬
‫א ‪ .‬הוכח ‪. AE  CE  DE 2 :‬‬
‫‪C‬‬
‫‪B‬‬
‫ב ‪ .‬הוכח ‪. AE  CE  PE 2 :‬‬
‫ג ‪ .‬הוכח ‪. DE  PE :‬‬
‫‪D‬‬
‫‪. 67‬‬
‫‪E‬‬
‫‪P‬‬
‫‪ AB‬הוא קוטר המעגל הגדול‬
‫ו‪ BC -‬הוא קוטר המעגל הקטן ‪.‬‬
‫‪ PC‬ו‪ AQ -‬משיקים למעגל הקטן ‪.‬‬
‫א ‪ .‬הוכח ‪. AP 2  AC  AB :‬‬
‫ב ‪ .‬הוכח ‪. AP  AQ :‬‬
‫‪A‬‬
‫‪C‬‬
‫‪B‬‬
‫‪Q‬‬
‫‪134‬‬