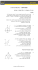המרחק בין שני ישרים מקבילים

‫המרחק בין שני ישרים מקבילים‬
‫בסעיף זה נציג נוסחה בעזרתה נחשב מרחק בין שני ישרים מקבילים‪.‬‬
‫תחילה נגדיר מרחק זה‪.‬‬
‫הגדרה‪ :‬מרחק בין שני ישרים מקבילים הוא אורך הקטע המאונך‬
‫לשני הישרים ומחבר נקודה על ישר אחד עם נקודה על הישר השני‪.‬‬
‫נתונים שני ישרים מקביל ים ‪ 1‬ו‪.  2 -‬‬
‫‪P‬‬
‫משוואת הישר ‪ 1‬הוא ‪. ax  by  c1  0‬‬
‫משוואת הישר ‪  2‬הוא ‪. ax  by  c 2  0‬‬
‫‪1‬‬
‫אורך הקטע ‪ PR‬שב ציור הוא המרחק‬
‫‪R‬‬
‫‪2‬‬
‫בין שני הישרים‪.‬‬
‫המרחק ‪ d‬שבין שני הישרים נתון בנוסחה הבאה‪:‬‬
‫| ‪| c1  c 2‬‬
‫‪a 2  b2‬‬
‫‪.d‬‬
‫נוכיח את הנוסחה עבור המקרים שבהם הישרים‬
‫‪y‬‬
‫אינם מקבילים לצירים ‪ .‬נשרטט ישר המאונך‬
‫לשני הישרים ועובר דרך ראשית הצירים‪.‬‬
‫‪P‬‬
‫הישר חותך את הישר ‪ 1‬ו‪ 2 -‬‬
‫בנקודות ‪ P‬ו‪ , R -‬בהתאמה‪.‬‬
‫‪1‬‬
‫אם נבודד את ‪ y‬נראה ששיפוע הישר ‪1‬‬
‫‪b‬‬
‫‪a‬‬
‫‪.‬‬
‫)והישר ‪ (  2‬הוא ‪ , ‬לכן שיפוע האנך הוא‬
‫‪a‬‬
‫‪b‬‬
‫‪R‬‬
‫‪2‬‬
‫‪x‬‬
‫בעזרת הנקודה )‪ (0;0‬נקבל שמשוואת הישר המאונך ה י א ‪b x‬‬
‫‪a‬‬
‫את שיעורי הנקודה ‪ P‬נק בל מפתרון מערכת המשוואות של‬
‫האנך ושל ‪: 1‬‬
‫הפתרון הוא‬
‫‪y  b x‬‬
‫‪‬‬
‫‪a‬‬
‫‪‬‬
‫‪ax  by  c1  0‬‬
‫‪bc ‬‬
‫‪ ac1‬‬
‫‪; 2 12 ‬‬
‫‪2‬‬
‫‪2‬‬
‫‪a b a b ‬‬
‫‪. P‬‬
‫את שיעורי הנקודה ‪ R‬נקבל מפתרון מערכת המשוואות‬
‫של האנך ושל ‪:  2‬‬
‫‪y  b x‬‬
‫‪‬‬
‫‪a‬‬
‫‪‬‬
‫‪ax  by  c 2  0‬‬
‫‪bc ‬‬
‫‪ ac 2‬‬
‫הפתרון הוא ‪; 2 2 2 ‬‬
‫‪2‬‬
‫‪2‬‬
‫‪a b a b ‬‬
‫‪. R‬‬
‫כל הזכויות שמורות ליואל גבע ואריק דז'לדטי‬
‫‪41‬‬
‫‪O‬‬
‫‪.y‬‬
‫נחשב את אורך הקטע ‪ PR‬לפי הנוסחה למרחק בין שתי נקודות‪.‬‬
‫‪2‬‬
‫נקבל‪:‬‬
‫‪2‬‬
‫‪ac    bc‬‬
‫‪ bc ‬‬
‫‪ ac‬‬
‫‪PR   2 1 2  2 2 2    2 1 2  2 2 2 ‬‬
‫‪a b  a b‬‬
‫‪a b ‬‬
‫‪a b‬‬
‫‪2‬‬
‫‪2‬‬
‫‪a 2 (c1  c 2 )2 b 2 (c1  c 2 )2‬‬
‫‪ a(c  c )   b(c  c ) ‬‬
‫‪PR   21 22    21 22  ‬‬
‫‪ 2‬‬
‫‪‬‬
‫‪(a 2  b 2 ) 2‬‬
‫‪(a  b 2 ) 2‬‬
‫‪ a b   a b ‬‬
‫| ‪(c1  c 2 ) 2 | c1  c2‬‬
‫) ‪(c1  c 2 ) 2 (a 2  b 2‬‬
‫‪(c1  c2 ) 2‬‬
‫‪‬‬
‫‪‬‬
‫‪‬‬
‫‪(a 2  b 2 ) 2‬‬
‫‪a 2  b2‬‬
‫‪a 2  b2‬‬
‫‪a 2  b2‬‬
‫‪PR ‬‬
‫‪y‬‬
‫הערה‪:‬‬
‫אם שני הישרים מקבילים‬
‫לציר ה‪ x -‬ומשוואותיהם ‪ y  k1‬ו‪, y  k 2 -‬‬
‫‪y  k2‬‬
‫‪y  k1‬‬
‫אז המרחק ‪ d‬ביניהם הוא ההפרש‬
‫בין ‪ k1‬ל‪ , k 2 -‬כלומר | ‪. d | k 2  k1‬‬
‫‪x‬‬
‫‪y‬‬
‫‪x  k1 x  k 2‬‬
‫באותו אופן‪ ,‬אם שני הישרים מקבילים‬
‫לציר ה‪ y -‬ומשוואותיהם ‪ x  k1‬ו‪, x  k 2 -‬‬
‫אז המרחק ‪ d‬ביניהם הוא ההפרש‬
‫‪x‬‬
‫בין ‪ k1‬ל‪ , k 2 -‬כלומר | ‪. d | k 2  k1‬‬
‫עם זאת‪ ,‬גם במקרים אלה‪ ,‬שהישרים מקבילים לציר ה‪ x -‬או לציר ה‪, y -‬‬
‫ניתן לחשב את המרחק ביניהם בעזרת הנוסחה למרחק בין שני ישרים‪.‬‬
‫דוגמה‪:‬‬
‫נתונות משוואות של שני ישרים מקבילים‪. x  2y  4  0 , x  2y  6  0 :‬‬
‫חשב את המרחק בין שני הישרים‪.‬‬
‫פתרון‪:‬‬
‫ניעזר בנוסחה למרחק בין שני ישרים מקבילים‪ .‬נקבל ‪ 10 :‬‬
‫‪5‬‬
‫המרחק הוא ‪ . 10‬אפשר לרשום גם ‪10  2  5  2 5‬‬
‫‪5‬‬
‫‪5‬‬
‫‪5‬‬
‫כל הזכויות שמורות ליואל גבע ואריק דז'לדטי‬
‫‪42‬‬
‫‪.‬‬
‫| )‪| 6  ( 4‬‬
‫‪2‬‬
‫‪1 2‬‬
‫‪2‬‬
‫‪.d‬‬
‫קביעת הסימן של המרחק בין שני ישרים מקבילים‬
‫ו‪.  2 -‬‬
‫נתונים שני ישרים מקבילים ‪1‬‬
‫משוואת הישר ‪ 1‬היא ‪. ax  by  c1  0‬‬
‫משוואת הישר ‪  2‬היא ‪. ax  by  c 2  0‬‬
‫ראינו כי המרחק ‪ d‬שבין שני הישרים הוא‬
‫| ‪| c1  c 2‬‬
‫‪a 2  b2‬‬
‫‪.d‬‬
‫בנוסחה מופיע ב מונה ) בתוך הערך המוחלט( הביטוי ‪. c1  c 2‬‬
‫ביטוי זה יכול לקבל ערך חיובי ויכול לקבל ערך שלילי )אם הביטוי‬
‫שווה לאפס‪ ,‬הישרים מתלכדים(‪ .‬אנו מכניסים את הביטוי לערך מוחלט‬
‫כדי לקבל בוודאות תוצאה חיובית‪ ,‬שהרי מרחק הוא גודל חיובי‪.‬‬
‫אם נדע מהו סימן הביטוי ‪ , c1  c 2‬נוכל לרשום את הנוסחה ללא‬
‫ערך מוחלט )נראה בהמשך שבחלק מהתרגילים זה יקל על הפתרון(‪.‬‬
‫כדי לדעת האם סימן הביטוי הוא חיובי או שלילי נפעל באופן הבא‪:‬‬
‫)‪(1‬‬
‫נרשום את משווא ו ת הישר ים המקבילים כך שהמקדם ‪ b‬של ‪y‬‬
‫הוא חיובי‪ .‬אם המקדם ‪ b‬הוא שלילי‪ ,‬נכפול את המשוואה ב‪. ( 1) -‬‬
‫) ‪ ( 2‬אם הישר ‪  2‬נמצא מעל הישר ‪ ,  1‬אז הביטוי ‪ c1  c2‬הוא חיוב י‬
‫ו הנוסחה למרחק בין שני הישרים היא‬
‫לעומת‬
‫‪c1  c 2‬‬
‫‪a 2  b2‬‬
‫‪.d‬‬
‫זאת‪ ,‬אם הישר ‪  2‬נמצא מתחת לישר ‪ ,  1‬אז הביטוי‬
‫הוא שלילי‬
‫ו הנוסחה למרחק בין שני הישרים היא‬
‫‪c1  c 2‬‬
‫‪a 2  b2‬‬
‫‪c1  c2‬‬
‫‪.d‬‬
‫למשל‪ ,‬בדוגמה הקודמת נתבקשנו לחשב את ה מרחק בין הישר ‪1‬‬
‫שמשוואתו ‪ , x  2y  6  0‬לבין הישר ‪  2‬שמשוואתו ‪. x  2y  4  0‬‬
‫ניתן לראות ש המקדם של ‪ y‬הוא חיובי‪ .‬אם נשרטט את הישרים‪,‬‬
‫נראה שהישר ‪ 2‬‬
‫נמצא מעל הישר ‪ , 1‬לכן הביטוי ‪ c1  c 2‬הוא חיובי‬
‫והנוסחה למציאת המרחק שבין שני הישרים היא‬
‫)‪6  ( 4‬‬
‫נציב בנוסח ה ונקבל‪ 10  2 5 :‬‬
‫‪5‬‬
‫‪1 2‬‬
‫‪2‬‬
‫‪2‬‬
‫‪c1  c 2‬‬
‫‪a 2  b2‬‬
‫‪.d‬‬
‫‪y‬‬
‫דוגמה‪:‬‬
‫נתון הישר ‪. y   1 x  1 1‬‬
‫‪3‬‬
‫‪6‬‬
‫מצא משוואת ישר המקביל‬
‫ל י שר הנתון ונמצא מעליו‬
‫במרחק ‪10‬‬
‫‪.d‬‬
‫‪x‬‬
‫ממנו‪.‬‬
‫כל הזכויות שמורות ליואל גבע ואריק דז'לדטי‬
‫‪y   13 x  1 16‬‬
‫‪43‬‬
‫פתרון‪:‬‬
‫תחילה נרשום את משוואת הישר הנתון בצורה ‪. ax  by  c  0‬‬
‫נ קבל‪ . 1 x  y  1 1  0 :‬אפשר )אם כי לא הכרחי( לכפול ב‪ 6 -‬את שני‬
‫‪3‬‬
‫‪6‬‬
‫האגפים‪ ,‬כדי לקבל מקדמים שלמים במשוואת הישר‪.‬‬
‫נעשה זאת ונקבל‪ . 2x  6y  7  0 :‬נרצה למצוא ישר המקביל לישר זה‪.‬‬
‫נסמן את הישר המקביל על ידי המשוו אה ‪. 2x  6y  c  0‬‬
‫דרך א'‪:‬‬
‫נביע את המרחק ש בין שני הישרים המקבילים בעזרת הנוסחה‬
‫)עם הערך המוחלט( ו נשווה את המרחק ל‪. 10 -‬‬
‫נקבל‪ 10 :‬‬
‫| ‪| 7  c‬‬
‫‪22  6 2‬‬
‫ומכאן ‪. | 7  c |  20‬‬
‫נקבל‪ 7  c  20 :‬או ‪ . 7  c  20‬הפתרונות הם ‪ c  27‬או ‪. c  13‬‬
‫משוואות הישרים הן ‪ 2x  6y  13  0‬או ‪. 2x  6y  27  0‬‬
‫מבין שני הישרים‪ ,‬רק הישר ‪ 2x  6y  27  0‬נמצא מע ל הישר הנתון‪,‬‬
‫לכן הוא הישר המבוקש‪ .‬אפשר לבודד את ‪ y‬ולקבל ‪. y   1 x  4 1‬‬
‫‪3‬‬
‫‪2‬‬
‫דרך ב '‪:‬‬
‫נפתור ללא ערך מוחלט‪ .‬המקדם של ‪ y‬חיובי בשתי המשוואות‪.‬‬
‫הישר המבוקש ‪ 2x  6y  c  0‬נמצא‬
‫לכן המרחק בין שני הישרים הוא‬
‫נקבל‪7  c  10 :‬‬
‫‪22  6 2‬‬
‫מעל‬
‫היש ר הנתון ‪, 2x  6y  7  0‬‬
‫‪7  c‬‬
‫‪2 2  62‬‬
‫‪ .‬נשווה ל‪. 10 -‬‬
‫ומכאן ‪ . c  27‬משוואת הישר היא ‪. 2x  6y  27  0‬‬
‫תרגילים‬
‫‪.1‬‬
‫מצא את המרחק בין הישרים המקבילים הבאים‪:‬‬
‫א‪3x  4y  7  0 .‬‬
‫ב‪5x  12y  17  0 .‬‬
‫ג‪y  2x  17 .‬‬
‫‪3x  4y  8  0‬‬
‫‪5x  12y  22  0‬‬
‫‪y  2x  3‬‬
‫ד‪3x  y  0 .‬‬
‫ה‪x  4  0 .‬‬
‫‪6x  2y  40  0‬‬
‫‪.2‬‬
‫‪x60‬‬
‫ו‪.‬‬
‫‪y8  0‬‬
‫‪y20‬‬
‫נתון הישר ‪ . 3x  4y  7  0‬מצא את משוואות שני הישרים שהמרחק‬
‫של כל אחד מהם מהישר הנ תון הוא ‪. 2‬‬
‫‪.3‬‬
‫נתון ישר העובר דר ך הנקודה )‪ (0;4‬ויוצר זווית בת ‪ 45‬עם הכיוון‬
‫החיובי של ציר ה‪. x -‬‬
‫מצא את המשוואות של הישרים שמרחקם מהישר הנ תון הוא ‪. 3 2‬‬
‫כל הזכויות שמורות ליואל גבע ואריק דז'לדטי‬
‫‪44‬‬
‫‪.4‬‬
‫נתונים שני ישרים מקבילים‪. 5x  6y  14  0 , 5x  6y  8  0 :‬‬
‫מצא משוואת ישר המקביל להם ‪ ,‬עובר ביניהם ‪ ,‬ונמצא במרחק שווה‬
‫משניהם‪ ) .‬הערה‪ :‬ה ישר המבוקש נקרא המקביל האמצעי ( ‪.‬‬
‫‪.5‬‬
‫נתונים שני ישרים מקבילים‪. 5x  3y  2  0 , 5x  3y  4  0 :‬‬
‫מצא את ה משוואה של ישר שלישי המקביל לשניהם‪ ,‬ומרחקו מאחד‬
‫מהם שווה למרחק שביניהם )הבחן בין שני מקרים(‪.‬‬
‫‪.6‬‬
‫נתונים שני ישרים מקבילים‪. 5x  4y  5  0 , 5x  4y  7  0 :‬‬
‫מצא את המשוואה של ישר המקביל לשניהם‪ ,‬ומרחקו מהישר הראשון‬
‫גדול פי ‪ 2‬ממרחקו מהישר השני )הבחן בין שני מקרים( ‪.‬‬
‫‪.7‬‬
‫נתונות משוואות של שני ישרים‪. x  my  3 , mx  4y  6 :‬‬
‫א‪ .‬מצא לא יזה ערך של ‪ m‬הישרים מקבילים ‪.‬‬
‫ב‪ .‬עבור הערך של ‪ m‬שמצאת ‪ ,‬חשב את המרחק שבין שני הישרים‪.‬‬
‫‪.8‬‬
‫נתונות משוואות של שני ישרים ‪:‬‬
‫‪x  ay  a‬‬
‫‪x  2y  2b‬‬
‫א ‪ .‬מצא לאילו ערכים של ‪ a‬ו‪ b -‬הישרים מקבילים זה לזה‪.‬‬
‫ב‪ .‬לאיזה ערך של ‪ b‬המרחק בין הישרים המקבילים הנ"ל הוא ‪? 5‬‬
‫‪.9‬‬
‫שתיים מצלעות יו של ריבוע מונחות על הישרים שמשוואותיהם‪:‬‬
‫‪ 3x  2y  2  0‬ו‪ . 3x  2y  28  0 -‬חשב את שטח הריבוע‪.‬‬
‫‪. 10‬‬
‫המשוואות של שתי צלעות סמוכות של ריבוע הן ‪3x  4y  9  0‬‬
‫ו‪ . 4x  3y  13  0 -‬אורך צלע הריבוע הוא ‪. 5‬‬
‫מצא את המשוואות של שתי הצלעות האחרות של הריבוע‪,‬‬
‫אם הנקודה )‪ (4; 2‬נמצאת בתוך הריבוע‪.‬‬
‫‪. 11‬‬
‫הגובה של מעוין הוא ‪ . 2 5‬המשוואות של שתיים מצלעותיו הן ‪y  2x  1‬‬
‫ו‪ . 2y  x  8 -‬מצא את המשוואות של שתי הצלעות האחרות במעוין‪,‬‬
‫אם ידוע שהנקודה )‪ (0; 2‬נמצאת בתוך המעוין‪.‬‬
‫‪. 12‬‬
‫המשוואה של אחת מצלעות מעוין היא ‪, 4x  3y  21  0‬‬
‫והמשוואה של אחד מאלכסוניו היא ‪ . 2y  x  6‬גובה המעוין הוא ‪. 4‬‬
‫מצא את קדקודי המעוין‪.‬‬
‫כל הזכויות שמורות ליואל גבע ואריק דז'לדטי‬
‫‪45‬‬
‫‪. 13‬‬
‫במקבילית ‪ ABCD‬נתון‪ . D( 2;1) , A(3;6) :‬שטח המקבילית הוא ‪. 55‬‬
‫א‪ .‬מצא את משווואת הישר עליו מונחת הצלע ‪ , BC‬אם הוא נמצא‬
‫מתחת לישר עליו מונחת הצלע ‪. AD‬‬
‫ב‪ .‬הנקודה ‪ B‬נמצאת ברביע ראשון ואורך הצלע ‪ AB‬הוא ‪. 11‬‬
‫מצא את שיעורי הקדקודים ‪ B‬ו‪. C -‬‬
‫‪. 14‬‬
‫במשולש שווה‪ -‬שוקיים‪ ,‬משוו את הבסיס היא ‪ x  2y  10  0‬והמשוואה‬
‫של אחת השוקיים היא ‪ . y  5.5x  0‬השוקיים נפגשות בראשית הצירים‪.‬‬
‫א‪ .‬מצא את משוואת השוק השנייה של המשולש‪.‬‬
‫ב‪ .‬בתוך המשולש‪ ,‬במרחק ‪5‬‬
‫מהבסיס‪ ,‬מעבירים י שר המקביל לבסיס‪.‬‬
‫מצא את משוואת הישר המקביל‪.‬‬
‫‪. 15‬‬
‫שלוש צלעות של המעוין ‪ ABCD‬נמצאות על הישרים הבאים‪:‬‬
‫הצלע ‪ AB‬על הישר ‪ , 3x  4y  7  0‬הצלע ‪ BC‬על הישר ‪, 12x  5y  8  0‬‬
‫הצלע ‪ CD‬על הישר ‪ . 3x  4y  3‬מצא את משוואת הישר שעליו נמצאת‬
‫הצלע הרביעית של המעוין‪ ,‬אם ידוע שהנקודה )‪ P(1; 2‬והצלע ‪AD‬‬
‫נמצאות בצדדים שונים של הישר ‪. BC‬‬
‫‪. 16‬‬
‫מצא את המשוואות של שני ישרים מקבילים‪ ,‬שאחד מהם עובר דרך‬
‫הנקודה )‪ (2; 2‬והאחר דרך הנקודה )‪ , (5; 21‬והמרחק ביניהם הוא ‪. 10‬‬
‫‪. 17‬‬
‫כל אחת מן הנקודות )‪ (0; 4‬ו‪ (6;6) -‬נמצאת על אחד משני ישרים מקבילים‪.‬‬
‫גם כל אחת מן הנקודות )‪ (1;1‬ו‪ (7;3) -‬נמצאת על אחד משני ישרים‬
‫מקבילים‪ .‬מצא את המשוואות של ארבעת הישרים‪ ,‬אם ידוע שנקודות‬
‫החיתוך שלהם הן קדקודים של ריבוע‪.‬‬
‫תשובות‪:‬‬
‫‪ . 1‬א‪ . 3 .‬ב‪ . 3 .‬ג‪ . 4 5 .‬ד‪ . 2 10 .‬ה‪ . 10 .‬ו‪. 3x  4y  17  0 . 2 . 6 .‬‬
‫‪. 3x  4y  3  0‬‬
‫‪. 5x  6y  3  0 . 4 . x  y  2  0 , x  y  10  0 . 3‬‬
‫‪ 5x  3y  10  0 . 5‬או ‪ 5x  4y  1  0 . 6 . 5x  3y  8  0‬או ‪. 5x  4y  17  0‬‬
‫‪ . 7‬א‪ . m  2 .‬ב‪6 .‬‬
‫‪5‬‬
‫‪. 2y  x  2  0 , y  2x  11 . 11 . 3x  4y  16  0 , 4x  3y  38 . 10‬‬
‫‪ . 8 .‬א‪ . b  1 , a  2 .‬ב‪ . b  3.5 .‬או ‪. b  1.5‬‬
‫‪. 52 . 9‬‬
‫‪ (9;5) , (4;5) , (7;9) , (12;9) . 12‬או )‪. (15;13) , (20;13) , (17;9) , (12;9‬‬
‫‪ . 13‬א‪ . y  x  8 .‬ב‪ . 14 . C(9;1) , B(14;6) .‬א‪. y  0.5x .‬‬
‫ב‪. x  2y  5  0 .‬‬
‫‪ y  3x  4 . 16 . 12x  5y  34  0 . 15‬ו‪ y  3x  6 -‬או ‪y  117x  236‬‬
‫ו‪y  0.5x  6.5 , y  0.5x  1.5 , y  2x  6 , y  2x  4 . 17 . y  117x  606 -‬‬
‫או ‪. y  0.5x  9 , y  0.5x  4 , y  2x  11 , y  2x  1‬‬
‫כל הזכויות שמורות ליואל גבע ואריק דז'לדטי‬
‫‪46‬‬
‫המרחק בין נקודה לישר‬
‫בסעיף זה נציג נוסחה בעזרתה נחשב מרחק של נקודה מישר‪.‬‬
‫הגדרה‪ :‬מרחק בין נקודה לישר הוא אורך האנך המורד מהנקודה לישר‪.‬‬
‫) ‪A(x1; y1‬‬
‫‪1‬‬
‫נתון ישר ‪ 1‬שמשוואתו ‪ax  by  c  0‬‬
‫ונתונה נקודה ) ‪ A(x1; y1‬שמחוץ לישר‪.‬‬
‫המרחק ‪ d‬שבין הנקודה ‪ A‬לישר ‪  1‬נתון בנוסחה‪:‬‬
‫| ‪| ax1  by1  c‬‬
‫‪a2  b2‬‬
‫‪d‬‬
‫נוכיח את הנוסחה‪.‬‬
‫דרך ) ‪ A(x1; y1‬נעביר ישר ‪  2‬המקביל לישר ‪. 1‬‬
‫משוואת הישר ‪ 2‬‬
‫‪2‬‬
‫היא ‪. ax  by  k  0‬‬
‫) ‪A(x1; y1‬‬
‫ה מרחק בין הנקודה ‪ A‬לישר ‪1‬‬
‫‪1‬‬
‫הוא למעשה המרחק בין הישרים‬
‫המקבילים ‪1‬‬
‫ו‪.  2 -‬‬
‫על פי הנוסחה למרחק בין שני ישרים מקבילים‬
‫המרחק בין ‪ 1‬ו‪ 2 -‬‬
‫הוא‬
‫|‪|ck‬‬
‫‪a 2  b2‬‬
‫‪ .‬הנקודה ) ‪ A(x1; y1‬נמצאת על‬
‫הישר ‪ ,  2‬לכן שיעוריה מקיימים את המשוואה ‪ ax  by  k  0‬של ‪.  2‬‬
‫נקבל‪ ax1  by1  k  0 :‬ומכאן ‪. k  ax1  by1‬‬
‫נציב במרחק‬
‫|‪|ck‬‬
‫‪a 2  b2‬‬
‫‪ .‬נקבל‪:‬‬
‫| ‪| ax1  by1  c‬‬
‫‪2‬‬
‫‪a b‬‬
‫‪2‬‬
‫‪‬‬
‫| ) ‪| c  (ax1  by1‬‬
‫‪2‬‬
‫‪a b‬‬
‫‪2‬‬
‫‪.d‬‬
‫דוגמה‪:‬‬
‫חשב את המרחק מהנקודה )‪ A(1; 1‬לישר ‪. 3x  2y  12  0‬‬
‫פתרון‪:‬‬
‫נציב בנוסחה למר חק בין נקודה ל ישר‪.‬‬
‫‪7‬‬
‫נקבל‪ 7 :‬‬
‫‪13‬‬
‫‪13‬‬
‫‪‬‬
‫| ‪| 3 1  2(1)  12‬‬
‫‪2‬‬
‫‪3 2‬‬
‫‪2‬‬
‫)‪A(1; 1‬‬
‫‪.d‬‬
‫‪B‬‬
‫המרחק בין הנקודה לישר הוא ‪7‬‬
‫‪13‬‬
‫‪.‬‬
‫שים לב! אפשר לחשב את המרחק בין הנקודה לישר גם ללא הנוסחה‪.‬‬
‫שיפוע הישר ‪ 3x  2y  12  0‬הוא ‪ , 3‬לכן שיפו ע האנך ‪ AB‬הוא ‪.  2‬‬
‫‪3‬‬
‫‪2‬‬
‫כל הזכויות שמורות ליואל גבע ואריק דז'לדטי‬
‫‪47‬‬
‫משוואת האנך המתקבלת היא ‪ . y   2 x  1‬נקודת החיתוך ‪ B‬של הישר‬
‫‪3‬‬
‫‪3‬‬
‫‪8‬‬
‫הנתון עם האנך ‪ AB‬היא ) ‪. B(2 ; 2 1‬‬
‫‪13‬‬
‫‪13‬‬
‫את המרחק ‪ AB‬נחשב לפי הנוסחה למרחק בין שתי נקודות‪ ,‬ונקבל ‪7‬‬
‫‪13‬‬
‫הערה‪:‬‬
‫‪.‬‬
‫כאשר הישר מקביל או מאונך לאחד הצירים אפשר לחשב‬
‫את המרחק של הנקודה ) ‪ (x1; y1‬ממנו גם ללא הנוסחה באופן הבא‪:‬‬
‫) ‪ ( 1‬אם הישר מק ביל לציר ה‪ x -‬ומשוואתו ‪ , y  k‬ה מרחק הוא | ‪. | y1  k‬‬
‫) ‪ ( 2‬אם הישר מקביל לציר ה‪ y -‬ומשוואתו ‪ , x  k‬ה מרחק הוא | ‪. | x1  k‬‬
‫קביעת ה סימן של המרחק בין הנקודה לישר‬
‫בנוסחה למציאת מרחק של נקודה ) ‪ (x1; y1‬מהישר ‪ax  by  c  0‬‬
‫מופיע ב מונה ) בתוך הערך המוחלט( הביטוי ‪. ax1  by1  c‬‬
‫ביטוי זה יכול לקבל ערך חיובי ויכול לקבל ערך שלילי )אם הערך‬
‫הוא אפס ‪ ,‬הנקודה נמצאת על הישר( ‪ .‬אנו מכניסים את הביטוי לערך‬
‫מוחלט כדי לקבל בוודאות תוצאה חיובית‪ ,‬שהרי מרחק הוא גודל חיובי‪.‬‬
‫אם נדע מהו סימן הביטוי ‪ , ax1  by1  c‬נוכל לרשום את הנוסחה ללא‬
‫ערך מוחלט )נראה בהמשך שבחלק מהתרגילים זה יקל על הפתרון(‪.‬‬
‫כדי לדעת האם סימן הביטוי הוא חיובי או שלילי נפעל באופן הבא‪:‬‬
‫)‪(1‬‬
‫נרשום את משוואת הישר ‪ ax  by  c  0‬כך שהמקדם ‪ b‬של ‪y‬‬
‫הוא חיובי‪ .‬אם המקדם ‪ b‬הוא שלילי‪ ,‬נכפול את המשו ואה ב‪. ( 1) -‬‬
‫)‪(2‬‬
‫אם הנקודה מעל הישר‪ ,‬אז הביטוי ‪ ax1  by1  c‬הוא חיובי‬
‫ו הנוסחה למרחק הנקודה מהישר היא‬
‫‪ax1  by1  c‬‬
‫‪a 2  b2‬‬
‫‪.d‬‬
‫לעומת זאת‪ ,‬אם הנקודה מתחת לישר ‪ ,‬אז הביטוי ‪ax1  by1  c‬‬
‫הו א שלילי ו הנוסחה למרחק הנקודה מהישר היא‬
‫‪ax1  by1  c‬‬
‫‪a 2  b2‬‬
‫‪.d‬‬
‫למשל‪ ,‬בדוגמה הקודמת נתבקשנו לחשב את מרחק הנקודה )‪(1; 1‬‬
‫מהישר ‪ . 3x  2y  12  0‬נרצה לכתוב את הנוסחה ללא ערך מוחלט ‪,‬‬
‫לכן נכפול את המשוואה ב‪ ( 1) -‬כדי שהמקדם של ‪ y‬יהיה חיובי‪.‬‬
‫נקבל ‪. 3x  2y  12  0 :‬‬
‫הנקודה‬
‫)‪ A(1; 1‬נמצאת מעל הישר‬
‫) אפשר להוכיח זאת על ידי הצבת‬
‫הנקודה במשוואת הישר(‪ ,‬לכן הנוסחה למרחק הנקודה מהישר‬
‫‪ax  by1  c‬‬
‫‪7‬‬
‫היא‬
‫‪ . d   1‬נציב ו נקבל‪:‬‬
‫‪13‬‬
‫‪a 2  b2‬‬
‫כל הזכויות שמורות ליואל גבע ואריק דז'לדטי‬
‫‪48‬‬
‫‪‬‬
‫‪3 1  2  (1)  12‬‬
‫‪2‬‬
‫‪(3)  2‬‬
‫‪2‬‬
‫‪.d‬‬
‫מציאת המרחק על פי הנקודה והישר – תרגילים‬
‫‪.1‬‬
‫מצא את המרחק של הנקודה )שמשמאל( מהישר )שמימין(‪:‬‬
‫א‪, 3x  4y  8  0 .‬‬
‫ג‪, y  3x  4 .‬‬
‫ב‪, 12x  5y  7  0 .‬‬
‫)‪(4;5‬‬
‫ד‪, y   8 x  1 .‬‬
‫‪15‬‬
‫‪15‬‬
‫)‪(7; 5‬‬
‫ה‪(6;3) , x  2 .‬‬
‫‪.2‬‬
‫)‪(2; 7‬‬
‫)‪(3; 4‬‬
‫ו‪(1; 5) , y  4 .‬‬
‫נתון ישר העובר דרך הנקודה )‪ A( 2;4‬ויוצר זווית בת ‪ 45‬עם הכיוון‬
‫החיובי של ציר ה‪ . x -‬חשב את מרחקו של הישר מראשית הצירים‪.‬‬
‫‪.3‬‬
‫מבין כל הנקודות ה נמצאות ע ל הישר ‪ , 3x  2y  9  0‬הנקודה ‪A‬‬
‫היא ה קרובה ביותר לנקודה )‪ . B(  4;9‬מהו המרחק ‪? AB‬‬
‫‪.4‬‬
‫במשולש ‪ ABC‬נתון‪. C(5;1) , B(1;3) , A(4;5) :‬‬
‫חשב את אורך הגובה לצלע ‪. BC‬‬
‫תשובות‪:‬‬
‫‪ . 1‬א‪ . 8 .‬ב‪ . 4 .‬ג‪ . 3 10 .‬ד‪ . 5 .‬ה‪ . 4 .‬ו‪7 5 . 4 . 3 13 . 3 . 3 2 . 2 . 9 .‬‬
‫‪5‬‬
‫מציאת נקודה על פי מרחקה מישר‬
‫דוגמה‪:‬‬
‫מצא נקודה הנמצאת על הישר ‪ y  x  2‬ברביע השלישי ומרחקה מהישר‬
‫‪ y  3x  10‬הוא ‪40‬‬
‫‪.‬‬
‫פתרון‪:‬‬
‫נסמן על הישר ‪ y  x  2‬נקודה ‪. A‬‬
‫נוריד ממנה אנך לישר ‪. y  3x  10‬‬
‫על פי הנתון‪ ,‬אורך האנך הוא ‪40‬‬
‫)‪A(t; t  2‬‬
‫‪.‬‬
‫‪40‬‬
‫במקרה זה ידועה משוואת הישר ‪, y  3x  10‬‬
‫ידוע המרחק ‪40‬‬
‫שבין הנקודה לישר‬
‫‪y  3x  10‬‬
‫ועלינו למצוא את שיעורי הנקודה ‪. A‬‬
‫נקודה ‪ A‬נמצאת על הישר ‪ , y  x  2‬לכן נוכל לסמנה )‪. A(t; t  2‬‬
‫את הישר נרשום באופן הבא‪. 3x  y  10  0 :‬‬
‫נביע את מרחק הנקודה ‪ A‬מהישר ‪ 3x  y  10  0‬ונשווה אותו ל‪40 -‬‬
‫כל הזכויות שמורות ליואל גבע ואריק דז'לדטי‬
‫‪49‬‬
‫‪.‬‬
‫‪.‬‬
‫| ‪| 2t  12‬‬
‫| ‪| 3t  (t  2)  10‬‬
‫‪ ,‬כלומר ‪ 40‬‬
‫נקבל‪ 40 :‬‬
‫‪10‬‬
‫‪(3) 2  12‬‬
‫ומכאן ‪. | 2t  12 |  20‬‬
‫נקבל‪ 2t  12  20 :‬או ‪. 2t  12  20‬‬
‫‪ t  16‬או‬
‫‪t4‬‬
‫הפתרון ‪ t  4‬אינו מתאים לנתון לפיו הנקודה ברביע השלישי‪.‬‬
‫עבור ‪ t  16‬נקבל )‪ , A( 16; 18‬שנמצאת ברביע השלישי‪.‬‬
‫‪.5‬‬
‫מצא נקודה על ציר ה‪ , y -‬שמרחקה מהישר ‪ 3x  4y  20  0‬הוא ‪. 4‬‬
‫רשום את שתי האפשרויות‪.‬‬
‫‪.6‬‬
‫מצא נקודה על חלקו השלילי של ציר ה‪ , x -‬שמרחקה מהישר ‪y  2x  6‬‬
‫הוא ‪. 4 5‬‬
‫‪.7‬‬
‫מצא את שתי הנקודות הנמצאות על הישר ‪ , y  2x  3‬שמרחקן מהי שר‬
‫‪ 3x  4y  2  0‬הוא ‪. 6‬‬
‫‪.8‬‬
‫מרחקה של הנקודה )‪ ( 2;k‬מהישר ‪ 4x  3y  20  0‬הוא ‪. 4 1‬‬
‫‪2‬‬
‫מצא את הערך של ‪. (k  0) k‬‬
‫‪.9‬‬
‫מצא באיזה תחום צריך להיות ‪ k‬כדי שמרחקה של הנקודה )‪(k; 1‬‬
‫מהישר ‪ 5x  12y  9‬לא יהיה גדול מ‪. 8 -‬‬
‫‪13‬‬
‫‪. 10‬‬
‫שניים מקדקודי משולש ‪ ABC‬נמצאים בנקודות )‪ B(2;5‬ו‪. C(7;10) -‬‬
‫הקדקוד ‪ A‬נמצא על הישר ‪. y   x  15‬‬
‫אורך הגובה לצלע ‪ BC‬הוא ‪. 3 2‬‬
‫מצא את שיעורי הקדקוד ‪. A‬‬
‫‪. 11‬‬
‫מצא על ציר ה‪ y -‬את שתי הנקודות שמרחקן מהישר ‪7x  4y  10  0‬‬
‫שווה למרחקן מהישר ‪. x  8y  17  0‬‬
‫‪. 12‬‬
‫מצא על הישר ‪ y  2x  11‬את שתי הנקודות הנמצאות במרחק שווה‬
‫מהישרים ‪ 3x  y  2  0‬ו‪. x  3y  54  0 -‬‬
‫כל הזכויות שמורות ליואל גבע ואריק דז'לדטי‬
‫‪50‬‬
‫משוואות צלעותיו של משולש הן‪; 7y  4x  24  0 (AC) ; y  8x  12 (AB) :‬‬
‫‪. 13‬‬
‫)‪. 3x  4y  89  0 (BC‬‬
‫מצא נקודה בתוך המשולש הנתון‪ ,‬הנמצאת במרחקים שווים מהצלעות‬
‫‪ AB‬ו‪ , AC -‬ובמרחק ‪ 10‬מ ה צלע ‪. BC‬‬
‫צלעותיו של משולש הן‪; 2y  x  4 (AC) ; y  2x  1 (AB) :‬‬
‫‪. 14‬‬
‫)‪ . x  2y  28 (BC‬מצא נקודה בתוך המשולש‪ ,‬הנמצאת במרחקים‬
‫שווים מהצלעות ‪ AB‬ו‪ , AC -‬ומרחקה מהצלע ‪ BC‬גדול פי ‪ 2‬ממרחקה‬
‫מהצלע ‪. AC‬‬
‫תשובות‪:‬‬
‫‪ (0;10) . 5‬או )‪ (4;11) . 7 . ( 13;0) . 6 . (0;0‬או )‪. ( 8; 13‬‬
‫‪ (3;12) . 10 . 2.2  k  1 . 9 . k  3 1 . 8‬או )‪. (0;  7 ) , (0; 6.75) . 11 . (9;6‬‬
‫‪2‬‬
‫‪12‬‬
‫‪. (6;7) . 14 . (5; 6) . 13 . (5;21) , (3;17) . 12‬‬
‫מציאת משוואת ישר על פי מרחק נקודה נתונה ממנו‬
‫דוגמה‪:‬‬
‫מצא משוואת ישר המאונך לישר ‪ y  7x  6‬ומרחקו מהנקודה )‪(5;3‬‬
‫הוא ‪ . 2 2‬רשום את שתי האפשרויות‪.‬‬
‫פתרון‪:‬‬
‫ניעזר בנוסחה למציאת מרחק של נקודה מישר‪ .‬במקרה זה ידוע המרחק‬
‫ונתונה הנקודה‪ .‬עלינו למצוא את משוואת הישר‪.‬‬
‫‪.1‬‬
‫שיפוע הישר ‪ y  7x  6‬הוא ‪ , 7‬לכן שיפוע הישר המ בוקש הוא ‪7‬‬
‫‪1‬‬
‫‪.1‬‬
‫נסמן את הישר המבוקש ‪ , y   7 x  b‬כלומר ‪7 x  y  b  0‬‬
‫נביע את מרחק הנקודה )‪ (5;3‬מישר זה ונשווה את המרחק ל‪. 2 2 -‬‬
‫‪1 5  3  b‬‬
‫‪7‬‬
‫‪ ,‬כלומר ‪. 3 75  b  2 76‬‬
‫נקבל‪ 2 2 :‬‬
‫‪1 2  12‬‬
‫‪7‬‬
‫‪ ‬‬
‫נקבל‪ 3 75  b  2 76 :‬או ‪. 3 75  b  2 76‬‬
‫‪ b  76‬או ‪b  6 74‬‬
‫‪6‬‬
‫‪4‬‬
‫‪1‬‬
‫‪. y1‬‬
‫לסיכום‪ ,‬משוואת הישר המבוקש היא ‪ y   7 x  7‬או ‪7 x  6 7‬‬
‫כל הזכויות שמורות ליואל גבע ואריק דז'לדטי‬
‫‪51‬‬
‫‪. 15‬‬
‫מצא משוואת ישר‪ ,‬ששיפועו ‪ 3‬ומרחקו מהנקודה )‪ (4;1‬הוא ‪. 2 10‬‬
‫‪. 16‬‬
‫מצא את המשוואה של ישר‪ ,‬המקביל לישר ‪ 3x  4y  70  0‬ומרחקו‬
‫מהנקודה )‪ (5; 2‬הוא ‪. 7‬‬
‫‪. 17‬‬
‫מרחק הנקודה )‪ (6;7‬מהישר ‪ (k  2)x  4ky  k  13  0‬הוא ‪ . 8‬מצא את ‪. k‬‬
‫‪. 18‬‬
‫האורך של אחת הצלעות במלבן הוא ‪ , 2 5‬ואורך הצ לע האחרת הוא ‪. 4 5‬‬
‫אלכסוני המלבן נפגשים בנקודה )‪ , (5; 7‬והצלעות הארוכות של המלבן‬
‫מקבילות לישר ‪ . y  2x‬מצא את המשוואות של צלעות המלבן‪.‬‬
‫‪. 19‬‬
‫המשוואה של אחת הצלעות בריבוע היא ‪ , x  3y  5  0‬ונקודת החיתוך‬
‫של אלכסוניו היא )‪. M( 1;0‬‬
‫מצא את המשוואות של הצלעות האחרות בריבוע‪.‬‬
‫‪. 20‬‬
‫שתי צלעות של ריבוע מקבילות לישר ‪ 5x  12y  1  0‬וכל אחת מהן‬
‫נמצאת במרחק ‪ 5‬יחידות ממנו‪.‬‬
‫נקודת המפ גש של אלכסוני הריבוע היא )‪. M(5  2‬‬
‫מצא את משוואות הישר י ם שעליהם נמצאות צלעות הריבוע‪.‬‬
‫‪. 21‬‬
‫המשוואות של שתי צלעות של ריבוע הן ‪ x  2y  9‬ו‪. x  2y  19 -‬‬
‫אלכסוני הריבוע נפגשים על הישר ‪. x  4‬‬
‫מצא את המשוואות של הצלעות האחרות של הריבוע‪.‬‬
‫דוגמה‪:‬‬
‫מצא את המשוואה של ישר העובר דרך הנקודה )‪A(7;6‬‬
‫ומרחקו מהנקודה )‪ B(4;5‬הוא ‪. 3‬‬
‫פתרון‪:‬‬
‫‪y‬‬
‫נעביר אנך מנקודה ‪ B‬לישר המבוקש‪.‬‬
‫נסמן ב‪ C -‬את נקודת החיתוך בין האנך לישר‪.‬‬
‫‪C‬‬
‫)‪A(7;6‬‬
‫נפתור בשתי דרכים‪.‬‬
‫דרך א' –‬
‫)‪B(4;5‬‬
‫ניעזר בנוסחה למרחק נקודה מישר‪.‬‬
‫נתונה הנקודה )‪ B(4;5‬וידוע מרחקה מהישר‬
‫המבוקש‪ .‬כדי להיעזר בנוסחה של מרחק‬
‫נקודה מ ישר עלינו לרשום את משוואת הישר‪.‬‬
‫כל הזכויות שמורות ליואל גבע ואריק דז'לדטי‬
‫‪52‬‬
‫‪3‬‬
‫‪x‬‬
‫ידוע כי הישר המבוקש עובר דרך הנקודה )‪ , A(7;6‬לכן נסמן ב‪ m -‬את‬
‫שיפוע הישר ונמצא את ‪. m‬‬
‫נדגיש כי בדרך זו יכולים להתקבל רק ישרים בעלי שיפוע‪ ,‬כלומר‬
‫ישר ה מאונך לציר ה‪) x -‬ששיפועו לא מוגדר( לא יכול להתקבל ויש‬
‫לבדוק בנפרד האם קיים ישר כזה המקיים את דרישות השאלה‪.‬‬
‫נסמן ב‪ m -‬את שיפוע הישר המבוקש‪ ,‬העובר דרך הנקודה )‪. (7;6‬‬
‫נקבל שמשוואת הישר הי א‪ , y  6  m(x  7) :‬כלומר ‪. y  mx  6  7m‬‬
‫נרשום את משוואת הישר בצורה הכללית‪. mx  y  6  7m  0 :‬‬
‫נביע את מרחקה של הנקודה )‪ (4;5‬מהישר ונשווה את המרחק ל‪. 3 -‬‬
‫נקבל‪ 3 :‬‬
‫| ‪| m  4  5  6  7m‬‬
‫‪m 2  (1) 2‬‬
‫‪ ,‬כלומר ‪ 3‬‬
‫| ‪|1  3m‬‬
‫‪m 1‬‬
‫‪2‬‬
‫ומכאן ‪. |1  3m |  3 m 2  1‬‬
‫נעלה בריבוע את שני האגפים‪.‬‬
‫נקבל‪ , (1  3m) 2  9(m 2  1) :‬כלומר ‪1  6m  9m  9m  9‬‬
‫‪2‬‬
‫‪2‬‬
‫ומכאן ‪ . 6m  8‬פתרון המשוואה הוא ‪. m  1 1‬‬
‫‪3‬‬
‫משוואת הישר היא ‪. y  mx  6  7m‬‬
‫נציב ‪ m  1 1‬ונקבל ‪ . y  1 1 x  15 1‬אפשר לרשום גם ‪. 4x  3y  46  0‬‬
‫‪3‬‬
‫‪3‬‬
‫‪3‬‬
‫נעבור לבדוק האם קיים ישר המאונך לציר ה‪ x -‬העובר דרך הנקו דה )‪(7;6‬‬
‫ומרחקו מהנקודה )‪ (4;5‬הוא ‪. 3‬‬
‫משוואת הישר המאונך לציר ה‪ x -‬ועובר דרך‬
‫‪y‬‬
‫‪x7‬‬
‫הנקודה )‪ (7;6‬היא ‪ . x  7‬בעזרת מ ערכת צירים‬
‫אפשר לראות ש מרחקו של ישר זה מהנקודה )‪(4;5‬‬
‫‪C‬‬
‫‪A‬‬
‫הוא ‪ , 7  4‬כלומר ‪ 3‬ולכן גם ישר‬
‫‪B‬‬
‫‪4x  3y  46  0‬‬
‫זה מקיים את דרישת השאלה‪.‬‬
‫לסיכום‪ ,‬משוואות הישרים המבוקשים‬
‫‪x‬‬
‫הם ‪ 4x  3y  46  0‬ו‪) x  7 -‬ראה ציור משמאל( ‪.‬‬
‫דרך ב '‬
‫– נסמן )‪ C(t;m‬ונרכיב שתי משוואות שהנעלמים הם ‪ t‬ו‪. m -‬‬
‫) ‪ ( 1‬המרחק ‪ BC‬שווה ל‪. 3 -‬‬
‫ניעזר בנוסחה למרחק בין שתי נקודות‪ .‬נקבל‪. (t  4)  (m  5)  3 :‬‬
‫‪2‬‬
‫‪2‬‬
‫) ‪ ( 2‬הקטעים ‪ AC‬ו‪ BC -‬מאונכים זה לזה‪ ,‬כלומר מכפלת השיפועים‬
‫של ‪ AC‬ו‪ BC -‬שווה ל‪ . 1 -‬נקבל‪m  6  m  5  1 :‬‬
‫‪t 7 t 4‬‬
‫‪.‬‬
‫מפתרון מערכת המשוואות נקבל ‪. m  6.8 , t  6.4‬‬
‫לפי שיעורי הנקודות ‪ A‬ו‪ C -‬אפשר למצוא את משוואת הישר ‪. AC‬‬
‫נקבל ‪ . 4x  3y  46  0‬גם כאן נ בדוק האם קיים ישר המאונך לציר ה‪x -‬‬
‫כל הזכויות שמורות ליואל גבע ואריק דז'לדטי‬
‫‪53‬‬
‫העובר דרך הנקודה )‪ (7;6‬ומרחקו מהנקודה )‪ (4;5‬הוא ‪. 3‬‬
‫כפי שתואר בדרך א' גם כאן נקבל את הישר ‪. x  7‬‬
‫הערה‪:‬‬
‫בדוגמה האחרונה אפשר לדעת מראש כמה ישרים מקיימים את‬
‫תנאי השאלה‪ .‬נסביר זאת‪.‬‬
‫הישר המבוקש ‪ AC‬נמצא במרחק ‪ 3‬מהנק ודה )‪ B(4;5‬וזהו המרחק‬
‫הקצר ביותר מהנקודה )‪ B(4;5‬לנקודה כלשהי שעל הישר‪.‬‬
‫הנקודה )‪ A(7;6‬נמצאת על הישר המבוקש‪.‬‬
‫נחשב את המרחק ‪ AB‬לפי הנוסחה למרחק בין שתי נקודות‪.‬‬
‫אם המר חק בין שתי הנקודות גדול מ‪ , 3 -‬אז קיימים שני ישרים‬
‫המקיימים את תנאי השאלה )ייתכן שאחד מהם מאונך לציר ה‪.( x -‬‬
‫אם המרחק בין שתי הנקודות שווה ל‪ , 3 -‬אז קיים ישר אחד המקיים‬
‫את תנאי השאלה )ייתכן והישר היחיד מאונך לציר ה‪.( x -‬‬
‫אם המרחק בין שתי הנקודות קטן מ‪ , 3 -‬אז לא קיים אף ישר המקיים‬
‫את תנאי השאלה‪.‬‬
‫בדוגמה הנ"ל המרחק ‪ AB‬הוא ‪. (7  4)  (6  5)  10‬‬
‫‪2‬‬
‫‪2‬‬
‫המרחק גדול מ‪ , 3 -‬לכן קיימים שני ישרים מתאימים‪.‬‬
‫כאשר הצבנו בנוסחה למרחק נקודה מישר קיבלנו רק ישר אחד‬
‫ומשוואתו ‪ . 4x  3y  46  0‬מאחר וצריכים להתקבל שני ישרים ‪" ,‬נחשוד"‬
‫שהישר השני המתקבל מאונך לציר ה‪ , x -‬ואכן בדקנו ו ראינו כי קיים‬
‫ישר המאונך לציר ה‪ x -‬המקיים את תנאי השאלה ומשוואתו ‪. x  7‬‬
‫‪. 22‬‬
‫מצא את המשוואה של ישר העובר בנקודה )‪ ( 2; 4‬ומרח קו מראשית‬
‫הצירים הוא ‪ . 10‬רשום את שתי האפשרויות‪.‬‬
‫‪. 23‬‬
‫מצא משוואת ישר העובר בנקודה )‪ (6;6‬ומרחקו מהנקודה )‪(5;3‬‬
‫הוא ‪ . 2 2‬כמה פתרונות יש לבעיה? נמק‪.‬‬
‫‪. 24‬‬
‫מצא משוואת ישר העובר בנקודה )‪ (5; 4‬ומרחקו מהנקודה )‪ (2;3‬הוא ‪. 3‬‬
‫‪. 25‬‬
‫מצא משוואת ישר העובר בנקודה )‪ (7; 6‬ומרחקו מהנקודה )‪ (2;1‬הוא ‪. 5‬‬
‫‪. 26‬‬
‫מצא את המשוואה של ישר העובר בנקודה )‪ (4; 2‬ומרחקו מראשית‬
‫הצירים הוא ‪. 2 5‬‬
‫‪. 27‬‬
‫מצא משוואת ישר העובר בנקודה )‪ (8;3‬ומרחקו מהנקודה )‪ (2;3‬הוא ‪. 6‬‬
‫כל הזכויות שמורות ליואל גבע ואריק דז'לדטי‬
‫‪54‬‬
‫‪. 28‬‬
‫האם קיים ישר העובר בנקודה )‪ (7; 2‬ומרחקו מהנקודה )‪ (5; 6‬הוא ‪? 5‬‬
‫‪. 29‬‬
‫מצא את המשוואה של ישר שמרחקו מהנקודה )‪ (4; 7‬הוא ‪ , 5‬אם נתון‬
‫שהישר עובר בנקודה‪:‬‬
‫א‪(3;6) .‬‬
‫‪. 30‬‬
‫ב‪(1; 3) .‬‬
‫ג‪(8;10) .‬‬
‫ד‪(9;7) .‬‬
‫ה‪(4; 2) .‬‬
‫ו‪(2; 4) .‬‬
‫הנקודה )‪ M(5; 2‬נמצאת במרחק ‪ 5‬מישר העובר דרך הנקודה )‪. A(1; 1‬‬
‫א‪ .‬מצא משוואת ישר זה‪.‬‬
‫ב‪ .‬מצא את שיעורי הנקודה הסימטרית ל‪ M -‬לגבי הישר שהתבקשת‬
‫למצוא בסעיף א'‪.‬‬
‫הדרכה ‪ :‬נקודה ‪ M1‬תהיה סימטרית לנקודה ‪ M‬לגבי ישר נתון‪,‬‬
‫אם הישר הוא אנך אמצעי של הקטע ‪. MM1‬‬
‫‪. 31‬‬
‫מצא משוואת ישר העובר דרך ראשית הצירים‪ ,‬אם סכום מרחקיו‬
‫מהנקודות )‪ (1; 7‬ו‪ (6; 2) -‬הוא ‪ 3 5‬והוא עובר בין הנקודות הנ"ל‪.‬‬
‫‪. 32‬‬
‫מצא משוואה של ישר שמרחקו מראשית הצירים הוא ‪ 5‬ומרחקו‬
‫מהנקודה )‪ (5;5‬הוא ‪. 4‬‬
‫‪. 33‬‬
‫במשולש ‪ ABC‬משוואות הצלעות ‪ AB‬ו‪ AC -‬הן‪ ,‬בהתאמה‪2x  y  5  0 ,‬‬
‫ו‪ . y  x  4 -‬אורכי הגבהים לצלעות ‪ AC‬ו‪ BC -‬הם‪ ,‬ב התאמה‪4.5 2 ,‬‬
‫ו‪ . 6 -‬מצא את שיעורי הקדקודים של המשולש‪ ,‬אם ראשית הצירים‬
‫נמצאת בתוך המשולש‪.‬‬
‫‪. 34‬‬
‫ישר )או ישרים( העובר בנקודה )‪ (7;8‬נמצא במרחק ‪ k‬מהנקודה )‪. (4;12‬‬
‫מצא לאילו ערכים של ‪ k‬מתקבלים‪:‬‬
‫א‪ .‬שני ישרים שאף אחד מהם אינו מאונך לציר ה‪. x -‬‬
‫ב‪ .‬שני ישרים שאחד מהם מאונך לציר ה‪. x -‬‬
‫ג‪ .‬ישר אחד בלבד‪.‬‬
‫ד‪ .‬אף ישר‪.‬‬
‫‪. 35‬‬
‫נת ון ריבוע שאורך אלכסונו ‪ 2a‬ואלכסוניו נמצאים על צירי השיעורים‪.‬‬
‫הוכח כי סכום ריבועי המרחקים של קדקודי הריבוע מישר כלשהו‪,‬‬
‫העובר דרך הראשית‪ ,‬שווה ל‪. 2a 2 -‬‬
‫‪. 36‬‬
‫הוכח את הנוסחה‬
‫‪c‬‬
‫‪A  B2‬‬
‫‪2‬‬
‫‪ d ‬למציאת מר חקו של הישר ‪Ax  By  C  0‬‬
‫מראשית הצירים‪.‬‬
‫כל הזכויות שמורות ליואל גבע ואריק דז'לדטי‬
‫‪55‬‬
‫תשובות‪:‬‬
‫‪ y  3x  9 . 15‬או ‪. y  3x  31‬‬
‫‪ 3x  4y  12  0 . 16‬או ‪. 3x  4y  58  0‬‬
‫‪ 3 . 17‬או ‪. x  2y  1  0 , x  2y  19  0 , y  2x  12 , y  2x  22 . 18 .  85‬‬
‫‪137‬‬
‫‪, 5x  12y  66 . 20 . 3x  y  3  0 , 3x  y  9  0 , x  3y  7  0 . 19‬‬
‫‪. y  2x  2 , y  2x  8 . 21 . 12x  5y  5 , 12x  5y  135 , 5x  12y  64‬‬
‫‪ y  3x  10 . 22‬או ‪ y   x  12 . 23 . x  3y  10  0‬או ‪ , y  1 x  36‬שני פתרונות‪.‬‬
‫‪7‬‬
‫‪7‬‬
‫‪ 4x  3y  32 . 24‬או ‪ x  7 . 25 . x  5‬או ‪. x  8 . 27 . y  2x  10 . 26 . y  6‬‬
‫‪ . 28‬לא קיים‪ . 29 .‬א‪ . 3x  4y  15  0 , 4x  3y  30  0 .‬ב‪, 3x  4y  9  0 .‬‬
‫‪ . x  1‬ג‪ . 4x  3y  62  0 .‬ד‪ . x  9 .‬ה‪ . y  2 .‬ו‪ .‬אין פתרון‪.‬‬
‫‪ . 30‬א‪ . 4x  3y  1  0 .‬ב‪ y  2x . 31 . ( 3; 4) .‬או ‪. y  0.5x‬‬
‫‪ 3x  4y  25  0 . 32‬או ‪. C(27;31) , B(0; 5) , A( 3;1) . 33 . 4x  3y  25  0‬‬
‫‪. 34‬‬
‫א‪ . k  3 , 0  k  5 .‬ב‪ . k  3 .‬ג‪ . k  5 .‬ד‪. k  5 .‬‬
‫שטח משולש על פי קדקודיו‬
‫בסעיף זה נראה כיצד מחשבים שטח של משולש לפי שיעורי שלושת‬
‫קדקודיו‪ .‬חישוב השטח נעשה בדרך כלל על ידי חישוב אורך של צלע‬
‫במשולש וחישוב של הגובה לאותה צלע‪.‬‬
‫דוגמה‪:‬‬
‫שטח ו של משולש ‪ ABC‬הוא ‪. 51.5‬‬
‫שיעורי שניים מקדקודיו הם )‪ A( 1; 10‬ו‪. B( 12; 2) -‬‬
‫מצא את שיעורי הקדקוד ‪ , C‬אם נתון שהוא נמצא על הישר ‪. y  2x  15‬‬
‫פתרון‪:‬‬
‫נחשב תחילה את אורך הצלע ‪ AB‬על פי הנוסחה למרחק בי ן שתי נקודות ‪.‬‬
‫נקבל‪AB  (1  12) 2  (10  2) 2  112  (8) 2  185 :‬‬
‫נסמן ב‪ h -‬את הגובה לצלע ‪ . AB‬נתון כי שטח המשולש ‪ ABC‬הוא ‪, 51.5‬‬
‫לכן ‪ , AB  h  51.5‬כלומר ‪103  103‬‬
‫‪AB‬‬
‫‪2‬‬
‫‪185‬‬
‫‪.h‬‬
‫‪y  2x  5 y‬‬
‫הגובה ‪ h‬הו א מרחק הקדקוד ‪ C‬מהישר ‪. AB‬‬
‫נמצא את משוואת הישר ‪. AB‬‬
‫)‪10  (2‬‬
‫‪.‬‬
‫שיפוע הישר ‪ AB‬הוא ‪  8‬‬
‫‪11‬‬
‫)‪1  (12‬‬
‫משוואת הישר ‪ AB‬ה י א )‪, y  2   8 (x  12‬‬
‫‪11‬‬
‫כל הזכויות שמורות ליואל גבע ואריק דז'לדטי‬
‫‪56‬‬
‫‪C‬‬
‫‪x‬‬
‫‪B‬‬
‫‪A‬‬
‫כלומר ‪ . y  2  8 x  8 8 .‬ומכאן ‪. y   8 x  10 8‬‬
‫‪11‬‬
‫‪11‬‬
‫‪11‬‬
‫‪11‬‬
‫נכפול את המשוואה ב‪. 11 -‬‬
‫נקבל‪ 11y  8x  118 :‬ומכאן ‪. 8x  11y  118  0‬‬
‫הקדקוד ‪ C‬נמצא על הי שר ‪ , y  2x  15‬לכן נוכל לסמנו )‪. C(t;2t  15‬‬
‫נביע את מרחק הקדקוד ‪ C‬מהישר ‪ AB‬ונשווה את התוצאה ל‪103 -‬‬
‫‪185‬‬
‫לא ידוע אם נקודה ‪ C‬נמצאת מעל או מתחת לישר‪ ,‬לכן ניעזר בערך‬
‫‪30t  283‬‬
‫‪8t  11(2t  15)  118‬‬
‫‪ ,‬כלומר ‪ 103‬‬
‫מוחלט‪ .‬נקבל‪ 103 :‬‬
‫‪2‬‬
‫‪2‬‬
‫‪185‬‬
‫‪185‬‬
‫‪185‬‬
‫‪8  11‬‬
‫‪.‬‬
‫ומכאן ‪. 30t  283  103‬‬
‫נקבל‪ 30t  283  103 :‬או ‪. 30t  283  103‬‬
‫‪. t  12 13‬‬
‫או‬
‫‪t  6‬‬
‫‪15‬‬
‫‪13‬‬
‫‪11‬‬
‫‪. 12 ; 10‬‬
‫‪15‬‬
‫שיעורי הקדקוד ‪ C‬הם )‪ ( 6;3‬או ‪15‬‬
‫‪‬‬
‫‪‬‬
‫תרגילים‬
‫‪.1‬‬
‫חשב את שטחי המשולשים ששיעור י הקדקודים שלהם הם‪:‬‬
‫א ‪. (4;7) , (10;3) , (2;1) .‬‬
‫‪.2‬‬
‫ב ‪. (2;11) , (5; 2) , ( 2;1) .‬‬
‫שטחו של משולש הוא ‪ , 28.5‬ושניים מקדקודיו הם )‪ (3;5‬ו‪. (12;8) -‬‬
‫מצא את שיעורי הקדקו ד השלישי‪ ,‬אם נתון שהוא נמצא על ציר ה‪. x -‬‬
‫רשום את שתי האפשרויות‪.‬‬
‫‪.3‬‬
‫הנקודות )‪ A(1;5‬ו‪ B(3; 4) -‬הן קדקודים במשולש ‪ , ABC‬שנמצא כו לו‬
‫ברביע הראשון‪ ,‬ושטחו ‪. 4.5‬‬
‫המשוואה של אחת מצלעות המשולש היא ‪. 2x  5y  23  0‬‬
‫א‪ .‬מצא את שיעורי הנקודה ‪. C‬‬
‫ב‪ AD .‬הוא הגובה לצלע ‪. BC‬‬
‫מהו היחס בין שטח המשולש ‪ ABD‬לשטח המשולש ‪? ACD‬‬
‫‪.4‬‬
‫שניים מקדקודיו של משולש ‪ ABC‬ששטחו ‪ 10.5‬הם )‪ A(5;6‬ו‪. B(2;2) -‬‬
‫הקדקוד הש לישי )‪ (C‬נמצא ברביע הרביעי על הישר ‪. y  x  6‬‬
‫א‪ .‬מצא את שיעורי הקדקוד ‪. C‬‬
‫ב‪ AD .‬הוא חוצה‪ -‬זווית של ‪. BAC‬‬
‫חשב את היחס בין שטח המשו לש ‪ ABD‬לשטח המשולש ‪. ACD‬‬
‫כל הזכויות שמורות ליואל גבע ואריק דז'לדטי‬
‫‪57‬‬
‫‪.5‬‬
‫במשולש שווה‪ -‬שוקיים ‪ , ABC‬קדקודי הבסיס הם )‪ C(3;0‬ו‪. B( 7; 2) -‬‬
‫הקדקוד השלישי של המשולש נמצא ברביע השני‪ .‬שטח המשולש הוא ‪. 26‬‬
‫א‪ .‬מצא את שיעורי הקדקוד ‪ A‬של ה משולש‪.‬‬
‫ב‪ .‬חשב את זווית הראש של המשולש‪.‬‬
‫‪.6‬‬
‫קדקוד של זווית הראש במשולש שווה‪ -‬שוקיים נמצא בנקודה )‪. ( 2; 6‬‬
‫בסיס המשולש מ ונח על הישר ‪ . y  2x  5‬שטח המשולש הוא ‪. 15‬‬
‫מצא את שני הקדקודים ה אחרים של המשולש‪.‬‬
‫‪.7‬‬
‫במשולש ישר‪ -‬זווית ‪ , (AC  BC) ABC‬נתון‪. B(11;3) , A(4;2) :‬‬
‫שטח המשולש הוא ‪. 7.5‬‬
‫מצא את קדקוד הזווית הישרה אם הוא נמצא מתחת ליתר ‪. AB‬‬
‫‪.8‬‬
‫במשולש ‪ , ABC‬ששטחו ‪ AD , 42‬הוא התיכון לצלע ‪. BC‬‬
‫א‪ .‬מה ו שטח המשולש ‪? ADC‬‬
‫ב‪ .‬נתון‪ D(5;8) , A(14; 2) :‬ומשוואת הצלע ‪ BC‬היא ‪. y  4x  12‬‬
‫מצא את שיעורי הנקודות ‪ B‬ו‪. C -‬‬
‫‪.9‬‬
‫שניים מקדקודי משולש ‪ ABC‬הם )‪ A(0;0‬ו‪. B(6; 2) -‬‬
‫תיכוני המשולש נפגשים בנקודה )‪. G(4;3‬‬
‫חשב את שטח המשולש ‪. ABC‬‬
‫‪. 10‬‬
‫‪y‬‬
‫במשולש ‪ ABC‬המתואר בציור‬
‫‪B‬‬
‫נתון‪. B(5;7) , A(1;1) :‬‬
‫‪D‬‬
‫הנקודה ‪ D‬נמצאת על הקטע ‪, AB‬‬
‫‪C‬‬
‫כך ש‪. SADC  2  SBDC -‬‬
‫‪A‬‬
‫‪x‬‬
‫מצא את שיעורי הנקודה ‪. D‬‬
‫‪. 11‬‬
‫במשולש ‪, ABC‬ששטחו ‪ 25.5‬התיכונים הם ‪ BE , AD‬ו‪. CF -‬‬
‫נתון‪ C(6; 3) , B(5; 2) :‬ו נקודת מפגש התיכונים )‪ (G‬נמצאת על ציר ה‪. x -‬‬
‫א‪ .‬מצא את שיעורי הקדקוד ‪ , A‬אם קדקוד זה ברביע השני‪.‬‬
‫ב‪ .‬הוכח‪. SACG  2  SAFG :‬‬
‫‪. 12‬‬
‫המשוואה של אחת מצלעות משולש היא ‪ . y  x  4‬שיעורי אחד‬
‫מקדקודי המשולש הם )‪ . (5; 7‬מפגש התיכונים הוא בנקודה ) ‪. (5 2 ;3 2‬‬
‫‪3 3‬‬
‫מצא את שיעורי שני הקדקודים האחרים של המשולש‪ ,‬אם נתון ששטח‬
‫המשולש הוא ‪. 18‬‬
‫כל הזכויות שמורות ליואל גבע ואריק דז'לדטי‬
‫‪58‬‬
‫‪. 13‬‬
‫שלושה קדקודים של משולש הם בנקודות )‪ ( 4; 1) , ( 1; 3‬ו‪. (a;1) -‬‬
‫מצא לאילו ערכים של ‪ a‬שטח המשולש קטן מ‪. 8 -‬‬
‫‪. 14‬‬
‫חשב את שטחו של מרובע ‪ ABCD‬ש קדקודיו הם )‪, B(5;5) , A( 2;3‬‬
‫)‪. D( 4; 3) , C(8; 1‬‬
‫‪. 15‬‬
‫ב מרובע ‪ ABCD‬נתון‪. D(2;1) , C(14;10) , B(7;9) , A(3;6) :‬‬
‫הוכח שהמרובע הוא טרפז וחשב את שטחו‪.‬‬
‫‪. 16‬‬
‫בטרפז ‪ (AB  CD) ABCD‬נתון‪, D( 2; 1) , C(10;3) , A( 1; 4) :‬‬
‫ושטח הטרפז הוא ‪. 35‬‬
‫מצא את שיעורי הנקודה ‪. B‬‬
‫‪. 17‬‬
‫שני קדקודי מקבילית הם )‪ (12;3‬ו‪ . (2;1) -‬המשוואה של אחת מצלעות‬
‫המקבילית היא ‪ y  2x  3‬ושטח המקבילית הוא ‪. 72‬‬
‫מצא את שיעורי שני הקדקודים האחרים של המקבילית‪.‬‬
‫‪. 18‬‬
‫)‪ B(8;7) , A(2;1‬ו‪ C(13;3) -‬הם קדקודי משולש‪ P .‬ו‪ Q -‬הן נקו דות‬
‫הנמצאות על הצלעות ‪ AB‬ו‪ , AC -‬בהתאמה‪ ,‬כך ש‪ PQ -‬מקביל ל‪. BC -‬‬
‫שטח המשולש ‪ APQ‬הוא ‪. 3‬‬
‫מצא את שי עורי הנקודות ‪ P‬ו‪. Q -‬‬
‫‪. 19‬‬
‫)‪ B( 9; 9) , A(16; 26‬ו‪ C( 4;16) -‬הם שיעורי הקדקודים של מ שולש ‪.‬‬
‫‪ P‬ו‪ Q -‬הן נקודות הנמצאות על הצלעות ‪ AB‬ו‪ , AC -‬בהתאמה‪,‬‬
‫כך ש‪ PQ -‬מקביל ל‪. BC -‬‬
‫שטח המרובע ‪ BPQC‬הוא ‪. 189‬‬
‫מצא את משוואת הי שר ‪. PQ‬‬
‫‪. 20‬‬
‫נקודות האמצע של צלעות משולש הן )‪. (5; 7) , (2;5) , (4;1‬‬
‫חשב את שטח המשולש‪.‬‬
‫‪. 21‬‬
‫במשולש ‪ ABC‬נתון‪ B(6; 2) , A(3; 6) :‬וקדקוד ‪ C‬נמצא על ציר ה‪. y -‬‬
‫מצא את שיעור י הקדקוד ‪ C‬ואת שטח המשולש ‪, ABC‬‬
‫אם נתון שאורך הגובה לצלע ‪ BC‬הוא ‪. 5‬‬
‫כל הזכויות שמורות ליואל גבע ואריק דז'לדטי‬
‫‪59‬‬
‫‪. 22‬‬
‫לשני משולשים יש קדקוד משותף והוא נמצא על ציר ה‪. x -‬‬
‫שני הקודקודים האחרים של משולש אחד הם )‪ (0; 4‬ו‪. (6;6) -‬‬
‫שני הקודקודים האחרים של המשולש האחר הם )‪ (4; 6‬ו‪. ( 4; 2) -‬‬
‫מצא את הקדקוד המשותף‪ ,‬אם סכום שטחי המשולשים הוא ‪. 34‬‬
‫תשובות‪:‬‬
‫‪ . 1‬א ‪ . 22 .‬ב ‪ (7; 0) . 2 . 41 .‬או )‪ . 3 . ( 31; 0‬א‪ . C(6;7) .‬ב‪. 1: 7 .‬‬
‫‪ . 4‬א‪ . (5; 1) .‬ב‪ . 5 . 5 : 7 .‬א‪ . ( 1; 6) .‬ב‪ (5;0) . 7 . (3;1) , (5;5) . 6 . 90 .‬או‬
‫)‪ . 8 . (10.6;0.8‬א‪ . 21 .‬ב‪. 15 . 9 . (6;12) , (4; 4) .‬‬
‫‪. a  7 , 15  a  1 . 13 . (9;5) , (3; 1) . 12‬‬
‫‪ . 11 . D(3 2 ;5) . 10‬א‪. ( 5;1) .‬‬
‫‪3‬‬
‫‪. 58 . 14‬‬
‫‪. (2;5) . 16 . 34 . 15‬‬
‫‪ (6;9) . 17‬ו‪ (16;11) -‬או )‪ (2; 7‬ו‪ (8; 5) -‬או )‪ (6;9‬ו‪ (8; 5) -‬או )‪(2; 7‬‬
‫ו‪ (0;5) . 21 . 32 . 20 . y  5x  18 . 19 . Q(5 23 ;1 23 ) , P(4;3) . 18 . (16;11) -‬ו‪7.5 -‬‬
‫או )‪ (0;35‬ו‪ (2; 0) . 22 . 37.5 -‬או‬
‫כל הזכויות שמורות ליואל גבע ואריק דז'לדטי‬
‫‪‬‬
‫‪‬‬
‫‪. 20 2‬‬
‫‪3 ;0‬‬
‫‪60‬‬